- 现代城市供配水系统优化调度的研究
-
企业: 控制网 日期: 2004-10-12 领域: 电源 点击数: 1643 吴惕华 张贵军 蔡满军
1 引言
水资源规划调度是一个古老的问题,可追溯到人类文明早期的防洪、供水活动中。人类社会早期文明(如中国、印度、欧洲以及中美洲)在一定程度上体现在他们对水资源管理及利用的能力上(Jay R. Lund, 2001)。随着人口集聚及城市的出现,使水资源供需之间的矛盾日见端倪,从而出现了早期的优化调度思想。早在古罗马时代人类就将定量分析和优化的思想应用在了水资源的规划上(Frontinus 97 AD,Leveau1993)。随着现代社会工业生产能力的提高,城市人口的不断增加及人们生活水平的不断改善,对城市供水系统的要求也越来越高,使城市供水管网规模及复杂性不断提高,传统经验调度方法不仅耗费了大量的能源(水、电能),而且使管网的压力分布极其不合理,已远不能满足人们对水资源的需求。我国(尤其是北方地区)是一个严重缺水的国家,数以百计的城市供水系统所采用的传统的恒压供水方式不仅浪费了大量的水资源,而且还消耗了大量的电能,即使如此,也不能满足人们的供水需求。因此,建立城市优化供水系统是我国为实施可持续战略急待解决的重大课题之一。
现代城市优化供水系统的设计目标是整个供水系统在全面蓄调的基础上实现经济调度和优化运行的目的,建立功能齐全、完整配套的集水源、制水、配水监控于一身的城市供水调度广域网络系统。建立合理有效的城市供配水优化调度数学模型是实现城市优化供水系统的关键,其建模内容一般包括原水的计划调度和实时调度、正常工作状态和非正常工作状态下的制水调度、配水计划调度和实时调度等三类。城市供水企业SCADA系统的推广及城市供配水管网GIS系统的相继建立、完善,为优化调度数学模型的数据准备提供了实现的可能;现代优化理论和方法的发展提供了优化调度建模的理论基础;计算机技术的发展为优化调度模型解算提供了实现上的保障。基于优化调度模型的城市供水系统结合企业生产过程的SCADA系统、企业现代化管理MIS/GIS系统和网络自动抄表收费AMR系统,组成了城市自来水综合自动化解决方案,从根本上解决城市优化供配水的问题。该方案是保证我国建成节水型城市,实现供水企业和国际接轨的重要措施。本文就有关建立城市供配水优化调度数学模型及算法仿真问题作一全面综述。
2 供配水系统优化运行的建模问题
城市供配水系统优化调度在不同的文献中有不同的定义[1~2],本文将所研究的优化调度定义为:根据供配水系统的历史记录和实时运行的信息,确定系统今后一个调度周期中各时间段内各种调节装置(如水泵的开停、闸阀的启闭,贮水池水位的升降等)的运行情况,在保证系统的服务质量(水量、水压和水质)下,最大限度的提高供水系统的经济效益和社会效益。
供配水系统优化运行的建模问题包括:供配水量预测模型、供配水网络分析模型及优化调度模型。用水量预测与需求分析属于优化运行实施的前期工作,也是进行供配水系统优化运行的基础和前提,它的准确程度直接影响到调度运行的可靠性及实用性[3];供配水网络分析模型与管网运行分析可以作为优化调度模型必要的约束条件;而最终的目的则是建立优化调度模型以实现供配水系统的优化运行。
2.1 供配水系统用水量预测模型
实际的供水调度中,主要是对日用水量和时用水量的预测。预测方法一般分为两类:解释性预测方法和时间序列预测方法。前者认为输入变量的变化会引起系统输出变量的变化,也就是说系统的输入和输出之间存在着某种因果关系。对于用水量的输入量一般要考虑气象、人口增长、工商业分布、居民活动及节假日作用等影响因素。这种模型对输入变量的精度要求较高,特别是当离线控制时,需要对次日整天的用水量进行预测,这就要求次日的天气、居民活动等预报资料精度较高,否则误差可能较大。后者是把系统当成一个黑箱,可以不管其影响因素,只关心观测和预测的结果,其预测过程只依赖于历史观测数据和它的数据模式。用水量预测中常用的模型有指数平滑模型、自回归(AR)模型[12]、滑动平均(ARMA)模型[3]、灰色预测模型[2]、动态组合预测模型[4]、自适应组合预测模型[5]、基于RBF神经网络模型[58]、模糊逻辑系统(FLS)和人工神经网络(ANN)[74]。此外,国外最新还研制出了基于环境和气候影响的用水量预测的决策支持系统(DSS)和分析模型[6]。另外,用水量预测在空间上可分为总水量预测和节点用水量预测。前者是指预测系统内每日或每时的用户用水量,这类预测采用的算法很多,它主要是为宏观模型的优化运行服务的;后者是预测分配到各系统节点的用水量,它的建模比较复杂,主要是为微观的模型服务的,国外一些发达国家在这方面进行了许多有益的探讨并进行了实际的应用[7~9]。
2.2 供配水系统网络分析模型
要对城市供水系统的运行进行优化调度决策,必须建立与供水系统的外部特征相吻合的数学模型,科学、准确、定量地描述系统中各个变量之间的关系。该模型可体现在供配水系统优化调度模型中的约束条件中。由优化调度的步骤可以看出,建立实际供水系统的网络分析模型是实现优化运行的先决条件。其中,供水系统中管网的分析和计算是两个重要模块。一方面通过对用户用水的要求,管网的管道的阻耗系数、配水泵的流量―扬程特性、管网的等水压线的分析、确定管网的合理布置、管径大小、管网测压线的分析;另一方面,针对已有管网分布及其特性建立管网的特性分析模型,用来分析管网对供水的影响。国内外学者在这方面进行了大量的研究,归纳起来大致可分为微观模型、宏观模型和管网集结模型。(1) 微观模型
微观模型是在尽可能考虑管网的拓扑结构及管网各元素(如管道管径、管长、管材等)、节点用水量等主要参数的水力学关系的基础上,构造出供水管网拓扑结构模型。这种模型的基本数学方程包括质量平衡和能量平衡两大部分,可用如下三个方程表示[2]:
节点方程: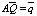 (1)
(1)回路方程:
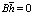 (2)
(2)压降方程:
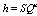 (3)
(3)目前,求解上述方程的方法已相当成熟,有节点水头法、环流量法和管段流量法等。以节点水压为求解变量的牛顿迭代法[67]为最有效的方法之一。
微观模型对系统的变化及节点用水量分布的变化适应性强,即便水池或主干管中断也只需将管网拓扑关系校正后仍可应用上述方程进行系统工况模拟仿真。但是,其缺点也很明显,需要大量的建模数据。应用上述微观模型的前提是已知管网各节点的节点流量及管道的摩阻系数;然而,节点流量是依赖用户用水量而随机变化的量,是最难以确定的值;管道摩阻系数受管道敷设年限、管道腐蚀及结垢等因素而发生变化,其变化值也难以解析;其次,模型的校核工作量大,计算时间长,耗费大。这些因素在一定程度上影响了微观模型的实际应用。
(2) 宏观模型
由美国学者Robert Demoyer Jr.[10]在1975年提出的,之后国内外许多的学者都致力于这项研究。这类模型的主要思想是利用获取的几种重要的管网参数(如测压点压力、泵站出口压力、泵站出水量、水池水位及系统的用水量等)以统计分析理论为基础,建立系统网络的(结构性)分析模型,其数学描述可表示为[3]: (4)
(4)(4)式右端一般为多项式,通过回归分析可确定具体的函数形式,论文[89]中给出了其中的一种函数形式。
管网宏观模型的特点是建模所需数据量少,建模快,计算效率高。但是适用范围有一定的限制,当系统用水量及其它已知参数变化幅度较大的时候,可能产生明显的误差。如当某水池或主干管中断时,宏观模型需要重新获取原始数据,进行回归分析、校正,建立新的模型形式。
(3) 管网集结模型
为了克服水系统管网微观模型的缺点并能充分利用宏观模型的优点,近年来提出了供水系统管网集结模型[11],该模型是建立在微观模型的基础上的。所谓管网集结其实就是一种简化网络结构的方法,它把整个配水管网划分为p个区域,使管网中每个节点必须且仅属于一个区域。通常区域的划分原则是:同区域内的各节点压力大致相等,用水规律相仿。将每个区域中的所有节点集结在一起,形成一个虚拟的节点,区域(即用虚拟节点组成的)之间的关联用一条虚拟的管道表示,这样原来的管网模型(微观模型)就简化为一个新的管网模型,称之为集结模型。集结模型不仅在计算上节约了计算时间,而且在建模上更科学合理且符合实际,对于多水库联合调度的问题其效果更加明显。该模型在宏观模型和微观模型之间提供了一种很好的折衷的方法。2.3 供配水系统优化调度模型
在供水系统的需水量和管网模型确定之后,就可以对系统供水进行优化调度。优化调度就是为已有的供水系统进行区域水量的分配及确定水泵的优化运行策略。具体就是在对调度日的城市用水量预测以后,利用建立的网络分析模型进行优化计算,得到调度日内各时段、各泵站的水泵开关策略及各种变速泵的转速。其目的就是在保证系统约束条件及给定的边界条件下,使给定的目标函数最小或者最大。对优化调度模型的目标函数的确定,国内大多数的学者是以费用最小[13~14]或者城市供水量最大[15~16]为目标的,而Jay R. Lund至少提出了6种在调度模型中可选的目标函数。根据所选择决策变量的不同还可将调度控制模型分为显式模型和隐式模型[2~3]。显式模型是直接以实际水泵的运行时间作为决策变量,而隐式模型则是首先采用中间变量,如泵站出口流量、水池变化轨迹等,并依此进行目标函数的寻优。3 供配水系统优化调度数学模型及算法
供配水优化调度是进行水量预测和管网分析的目的所在,也是本文重点。供配水系统优化调度首先是在城市用水量预测和管网分析的基础上,建立调度模型的目标函数以及相应的系统的约束条件,其中用水量预测和管网分析模型体现在其约束条件中,在满足约束的前提下,确定最优的目标函数。通过相应的约束条件,供配水系统的优化调度模型可以与水量预测模型和管网分析模型有机的集成在一起。
优化调度模型的目标函数是根据供水企业自身的费用、水源条件、环境、效益及国家的法规等多方面来确定的,Jay R. Lund在其论文中提出了6种调度模型中可选的目标函数类型[81]。不同的供水企业其制定的目标函数可能是不同的,根据实际的情况,还有可能进行多目标优化调度模型。通过权重标量化或者将目标函数转化为约束条件,可以将多目标优化模型转化为单目标模型,此外Jeffrey还采用了小生境排列遗传算法NPGA来解决多目标优化的问题[62]并成功应用在水力系统上。NPGA在选择算子中集成了显性排列(Pareto Domination)的概念并采用小生境技术,从而将群体分布在最优权衡排列面上。
优化调度模型的约束条件可以是供配水系统的水量预测模型、管网水力分析模型、目标函数或者是人为规定的一些政策法规、行业标准。约束条件的合理程度直接关系到系统优化调度的成败。
总的来说,优化调度模型的建立和其采用的算法是密不可分的。由上可知,优化调度模型的目标函数和约束条件在不同的场合是不同的,模型求解算法却是相对确定的,也就是说建立什么样的模型,可以有相应的算法来求解。基于这个原因,本文从优化调度的数学优化算法方面来阐述优化调度建模及实现方法,从中可得到有益的启迪。
供配水优化调度模型涉及到地上水、地下水、多水源多泵站的联合调度问题,是一个复杂的非线性系统。优化调度模型在求解的步骤上可分为直接优化调度模型[13]和多级优化调度供水调度模型[76,78],其中直接优化调度模型一般用来解决计算量比较小的管网系统,而对于变量比较多,计算量比较大的城市管网系统,则采用多级优化调度模型。
下面从传统的数学优化方法和现代优化算法两方面来介绍应用在供配水优化调度中优化算法以及相应的模型。
3.1 应用在供配水系统中的传统数学优化方法
在这里,传统的数学优化方法是指线性规划(LP)、整数规划(IP)、非线性规划(NLP)、动态规划(DP)以及最优控制理论(OCT)等优化方法。供配水优化调度模型是一个复杂的非线性系统。非线性的特征主要来源于泵站电耗、地下水水位的变化、管网水力方程、蒸发等因素。此外,基于决策的阶段特性(以日、时为调度时间),自然而然,非线性规划和动态规划的方法广泛的应用在供水优化调度的建模和模型的求解上。
(1) 线性规划(LP)、整数规划(IP)及最优控制原理(OCT)
LP方法主要是应用在模型的求解上,即将调度模型的非线性目标函数和约束条件转化为线性的约束条件,从而可以将非线性问题转化为线性问题来处理。常用线性化方法是Talor级数展开[57]、δ型逼近[25,75]、外部OA逼近[52]等。目前最新发展的LP是惩罚连续线性规划PSLP,通过连续的使用LP来求解NLP问题;同时Barker和Lasdon还提出了一种简化的PSLP方法[17],与传统连续线性规划SLP相比,这种方法能够更好的解决具有非线性约束条件的问题;Zhang 等人进一步改善了PSLP算法并论证了算法的收敛性[18]。在此基础上Hirad Mousavi应用PSLP算法解决了多水源联合供水系统的最优规划问题[57]。IP在供配水系统优化调度中的应用主要是针对一类具有固定费用约束的优化模型,该模型采用混合整数非线性规划(MINLP)[52]来描述供水系统优化调度问题。常用的解法是将MINLP转化为NLP[19~22]或者MILP[23~24]来求解优化模型。
OCT在供水系统调度模型中的应用并不多见,Mousavi已经证明其得到的解是一个次最优解[52];然而由于该算法对搜索起点的不敏感性,还是有一些学者成功地将OCT应用到水库的优化调度上[26~30]。
(2) 动态规划(DP)
基于优化调度是以日、小时为阶段来进行决策的,动态规划的方法广泛地应用在供水系统优化调度模型中[31~35]。其基本思想是在多阶段决策的过程中,把当前阶段和未来阶段分开,同时又将当前效益和未来效益结合起来考虑的一种最优化方法。对中小型的供水优化调度问题应用DP能够提出准确的最优解,但是随着模型阶数及变量数的增加,DP计算复杂性随维数的增加呈指数的增长。DP固有的两个问题限制了在供水优化调度中应用[58]:
? 维数灾:随模型维数的增加计算复杂性呈指数的增长;
? 模型灾:很难确定系统的模型、状态转移概率。(3) 非线性规划(NLP)
基于梯度的NLP优化算法广泛地应用在供水系统调度模型中。NLP能够求解一类光滑的非线性目标函数和约束条件的函数。建立相应的目标函数和约束条件后,在能保证模型精度的情况下,应用NLP方法建模,具有求解质量好的特点。现在能够求解上千个约束条件和变量的NLP软件包已经成功地应用在供水系统优化模型中,如MINOS[36]、CONOPT2[37]等。但是NLP本质上是一个局部寻优算法而不是一个全局寻优的算法,在应用上存在以下的限制[61]:
? NLP算法通常收敛到离搜索起点最近的局部最优点;
? 在原理上对非连续的问题并不能保证收敛性;
? 随系统的规模和复杂度的增加,计算速度和解的可靠性将降低。总之,传统的数学优化方法,从本质上都是一种局部、串行的计算方法。在简单的供配水优化调度系统中可能会取得很好的效果,但是随着系统复杂度的提高,模型的复杂度以及在求解速度、质量上都会受到一定的影响。由此限制了传统优化方法在许多供水系统中的成功应用。
3.2 应用在供配水系统中的现代优化算法
现代优化算法是80年代初兴起的启发式算法(Heuristic Algorithm)。这些算法包括禁忌算法(Tabu Search)、模拟退火(Simulated Annealing)、遗传算法(Genetic Algorithm)以及人工神经网络(Neural Network)。所谓的启发式算法是指一个基于直观或经验构造的算法,在可接受的花费(指计算时间、占用空间等)下给出待解决优化问题每一个实例的一个可行解,该可行解与最优解偏离程度不一定事先可以预计[38]。在某些情况下,特别是实际问题中,传统最优算法的计算时间使人无法忍受或因问题的难度使其计算时间随问题的规模的增加以指数速度增加,尤其是传统的最优算法本质上是一种串行、局部寻优算法。基于启发算法的并行性和全局寻优特性,为了解决上述传统的数学规划方法的局限性,这些算法在近几年开始应用于供水系统的优化调度问题中。在供水优化调度中应用最多的是遗传算法和模拟退火算法。也有将人工神经网络成功地应用在供水优化调度模型中[58][73],在该模型中M.Damas应用基于RBF网络的时序预测方法确定了供水调度系统不确定的输入变量。
(1) 遗传算法(GA)
GA是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化的概率算法。它最早是由美国密执安大学的Holland教授提出的,起源于60年代对自然和人工自适应系统的研究。70年代De Jong基于遗传算法的思想在计算机上进行了大量的纯数值函数优化计算实验。在一系列研究工作的基础上,80年代由Gold Berg进行归纳总结,形成了遗传算法的基本框架。GA已广泛地应用到供水系统的水量分配[39~42]、泵调度[43~45,83~85]、水池水位[39~45]以及管网恢复系统[46~47]等方面。GA是一种并行的全局寻优算法,应用该算法主要解决的问题是染色体的编码问题以及确定编码值是否满足模型的约束条件,即可行解。S.F.Beckwith 对此进行了讨论[45]。
由于GA算法本质上是一种仿生算法,由此对于一些复杂高阶系统的求解特别有效。在优化调度目标函数已经确定的前提下,其关键是选择适当的交叉算子(Crossover Operator)和变异算子(Mutation Operator)以及相应的编码和解码方法。其算法具有一定通用性。
此外,随着GA的发展,遗传编程(GP)也取得了很快的发展,从而在实现上提供了对GA的支持。如麻省理工学院Matthew Wall开发的GAlib,Andy Hunter开发的SUGAL等开发工具。应用这些中间算法库作为平台,可以很方便地开发出特定环境的遗传算法。
但是GA算法本身也存在一些局限性,如早熟现象、最优解附近收敛速度变慢等。对此,国内外一些学者已在进行研究[48]。研究结果表明,结合一些传统的优化方法,遗传算法可以取得更好的效果。
(2) 模拟退火算法(SA)
SA是Metropolis在1953年提出的,该算法是局部搜索算法的扩展,它不同于局部搜索之处是以一定的概率选择领域中费用值最大的状态。从理论上来说是一种全局最优化算法。在供水优化调度中应用参见文献[49~50,80]。3.3 应用在供配水系统中的混合优化方法
无论是传统的数学优化方法还是现代优化算法,单独应用在供配水优化调度问题上都有其自身的一些局限性。比如:传统的优化方法大都是一些局部寻优的算法,在实际应用中需要多次选择起点来进行测试,增加了算法的计算时间;而现代优化方法理论上是一种全局最优化算法,但是在最优点附近的收敛速度可能很慢等。国内外学者对这方面进行了许多的研究,提出了一些有效的供水系统优化调度模型及混合的优化算法。这类算法具有自适应性的特点,有效地克服了单一算法的局限性,提高了系统的计算效率及精度。1996年,Jean-Michel[51]提出了一种基于GA和爬山法的混合优化算法来进行全局的寻优,算法有效的结合了GA全局寻优特性及爬山法在最优点附近的收敛特性,在解的精确性、可靠性以及计算时间上取得了很好的折衷。2000年M.Damas[58]将此算法成功地应用到供水系统调度模型来确定一系列的可行解。
1997年,David W. Watkins Jr.[52]对供水系统中一类带固定费用问题的混合整数非线性规划(MINLP)调度模型应用两个分解算法GBD[53~54]和OA[55~56]对进行优化,得出了GBD适合大规模的调度模型的解算,而OA具有更快的收敛速度的结论。
1999年,Hirad Mousavi等[57]提出了一种PSLP-OCT供水优化运行模型。该模型应用最优控制原理OCT和惩罚连续线性规划PSLP的技术来对大规模复杂的供水系统进行优化。此外,为了实现费用最小以及尽可能满足供水需求,在模型中还应用了Epsilon约束的方法。
2000年,M.Damas等[58]提出了一种集混合遗传算法[51]和NDP[59]神经动态规划方法的供水网络优化调度模型。该模型主要是针对解决分阶段决策优化控制而提出的,其中每个阶段的状态变量和控制变量都是连续的。遗传算法采用混合遗传算法来确定每个决策阶段可行的状态变量;基于RBF神经网络[60]和经典的正交转换(SVD和QR)方法的时间序列预测来预测供水系统的阶段需水量;为了避免动态规划过程的灾数问题,利用Monte Carlo仿真的方法来逼近模型的最优值函数,以及采用并行计算的机群技术都大大提高了模型的计算时间和改善了计算效果。最后基于该模型成功地解决了西班牙Granada市供水网络优化调度的问题。
2001年,Ximing Cai[61]等提出了一种应用GA&LP来求解非线性水管理模型混合算法,其中GA用来确定模型的复杂变量,当其固定后,保持其余变量线性化,即可用LP的方法来求解,依此循环。在原理上GA算法可用其它的一些启发算法来求解,如禁忌算法TS和模拟退火SA来代替。
在供配水系统的优化调度模型中,还涉及到一类多目标优化的问题[87],对于这类的问题可以从两方面来解决:将一些目标函数转换为模型的约束条件;或应用多目标决策的方法来实现,如NPGA[62]的方法等。较为典型的是1999年Kato提出了一种交互式多目标的分层混合供水网络调度模型[63]。模型包括两层:抽象汇总调度层(ASP)和进一步的连续细节调度层(CDP)。ASP层确定每日供水总调度量,CDP层在此基础上进一步确定出一天中每小时水的调度量。在模型的求解中应用提出的混合多目标多阶段规划的方法HMMP,并与传统的多层网络模型的求解方法多阶段整数规划(MIP)[64]和完全的多目标规划(CMOP)在计算时间、水库的恢复率(RLR)以及流的平稳率(FSR)等方面成功地作了比较。测试结果表明,HMMP方法为已有的MIP和COMP提供了一种很好的中间规划方法。该模型还成功地应用到日本的某些城市供水调度中,验证了方法的可行性。文献[14,65~66,70]分别用不同算法实现了供水系统优化调度多目标优化的问题。
4 小结
综上所述,供配水系统优化调度模型是与用水量预测模型以及管网分析模型有机集合在一起的。在优化调度建模中可以将水量预测模型和管网分析模型转化为其约束条件,然后采用适当优化算法对模型进行求解。
采用传统的数学优化方法建立供配水系统优化调度模型,在系统比较简单的情况下,可以以较快的收敛速度得到较精确结果,但是现在供配水系统优化调度的模型已不局限于传统的单一泵站、水厂之间的供水调度,更多实现是多水源和多目标的联合调度模型,随着模型复杂性的提高,传统的数学优化方法无论在求解的有效性和精确性上还是在计算时间和计算资源的要求上,已远远不能满足要求。
采用一些现代优化算法可以在一定的程度上解决这个问题。比如遗传算法GA,单个个体的收敛速度虽然很慢,但是算法是基于整个群体,其并行性可以使收敛速度大大地提高,可获得全局优化;此外,算法对模型的要求也比较低,所有这些都大大促进了遗传算法在供配水系统中的广泛的应用。但是其也存在着一些问题,比如:求解初期的收敛速度很快,但是在后期的收敛速度却很慢,有时还必须采用适当的编码和选择算子以避免出现早熟现象。
为此,采用传统优化方法和现代优化算法相结合的方法建立和求解供配水系统优化调度模型有着广阔的前景。其中,管网分析模型可转化为模型的约束条件;采用并行的遗传算法可以很快地收敛到最优点的附近,然后应用线性规划等传统方法可很快收敛到调度模型的最优点,从而可以使群体不但并行地遗传进化,而且使群体中的个体有学习的过程,大大提高解的收敛速度和质量。
笔者在这方面的研究成果将另有专题论述,为城市供水系统优化调度提供一个有效的解决方案。
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



