- 吸引子键波与混沌系统同步关系的研究
-
企业: 控制网 日期: 2007-07-29 领域: PLC&PAC 点击数: 1841  兀旦晖(1981-)
兀旦晖(1981-)
男,陕西西安人,硕士,毕业于西安理工大学自动化与信息工程学院,主要研究领域为混沌在通信中的应用,现于陕西科技大学电气与电子工程学院从事教学科研工作。
基金项目:陕西省教育厅专项科研计划项目资助(05JK159); 陕西科技大学校级自然科学基金(2X05-41)
1 概述
混沌保密通信的研究在国际上起源于二十世纪九十年代初期,现已经历了十多年的时间,由于混沌信号自身所具有不可预测等特性,使得混沌保密通信具有极高的保密度,已成为目前信息科学界关注和研究的热点之一。混沌同步的发现,使得理论应用于通信领域成为可能,开始了混沌同步在保密通信中应用的新阶段。此后,国际上又相继提出了一些新的同步方法,主要有:一般性同步、相同步和一致性同步,其中一致性同步又可分为驱动—响应同步、误差—反馈同步、双向耦合同步、连续控制同步和自适应同步等,混沌同步问题之所以得到广泛的重视与研究,主要是它在混沌保密通信和扩频通信等领域显示出较好的应用前景,其中单向耦合同步在混沌通信中具有较大的应用价值。混沌系统同步对于混沌保密通信系统的实现以及信息传输速率的高低都有这极其重要的影响,所以,研究混沌同步有着重要的意义。
本文在改进型Chua电路的基础上,首先介绍了一种改进型Chua电路及其特性;分析了蔡氏电路中混沌吸引子的键波及螺旋表示方法;设计了一个基于Chua电路键波同步系统,通过实验给出了混沌系统同步与混沌吸引子键波之间的关系,为混沌同步系统在保密通信的实际应用奠定了一定的基础。
2 改进型Chua电路及其特性
1983年,蔡少棠教授首次提出了著名的蔡氏电路,它是迄今为止在非线性电路中产生复杂动力学行为的最有效而简单的混沌振荡电路之一,如图1所示。
图1 Chua 电路由两个线性电容C1和C2,一个线性电感 L ,一个线性电阻 R 和一个称之为Chua二极管的非线性电阻NR组成。从图中可以看到电路存在线性电感,由于其制作困难、体积大及分布参数的影响,难于集成,给电路带来不少困扰,影响了电路在实际中的应用。
文中给出了一种利用普通集成运放、线性电阻和电容组成的模拟电感电路,如图2所示。模拟电感电路是利用运算放大器的反馈和电容对电压的滞后作用,将电感元件用电容元件代替的电路,AB两端的等效电感为
L=C4R1R3R5 /R2 (1)
显然,改变式(1)中的电阻值,在AB两端可获得连续变化的电感量。
图2 模拟电感电路利用模拟电感电路对Chua电路进行改进,取代了Chua电路中的线性电感部分。构造出改进型Chua电路,取得了良好的效果,研究表明所有特性与原系统完全一致。
3 蔡氏电路中混沌吸引子的键波及螺旋表示
考虑一个三阶自治系统X=F(x),根据Shil’nikov定理,如果系统的平衡点XQ有一对稳定的复共轭特征值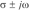 (
(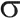 <0,w!=0)和一个不稳定的实特征值r(r>0),且
<0,w!=0)和一个不稳定的实特征值r(r>0),且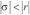 ,矢量场F(x)就会存在一条通过平衡点XQ的同宿轨道,然后通过改变系统的一个或多个参数而得到F的一个扰动F',这样F'就会存在横截同宿轨道和马蹄。横截同宿轨道的存在意味着存在无穷多的任意长周期的不稳定周期轨道。进一步意味着系统X=F(x)存在非周期解,即混沌轨道。
,矢量场F(x)就会存在一条通过平衡点XQ的同宿轨道,然后通过改变系统的一个或多个参数而得到F的一个扰动F',这样F'就会存在横截同宿轨道和马蹄。横截同宿轨道的存在意味着存在无穷多的任意长周期的不稳定周期轨道。进一步意味着系统X=F(x)存在非周期解,即混沌轨道。
蔡氏电路的状态方程可表示为
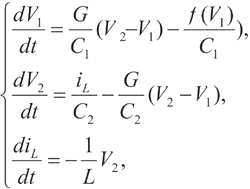
式中G=1/Rf(V1)=GbV1 + 0.5(Ga-Gb)[|V1+E|-|V1-E|],为蔡氏二极管NR的伏安特性函数,其中Ga=-0.76ms,Gb=-0.41ms,E=1V。
根据非线性电阻NR的分段线性的特性,蔡氏电路矢量场可分为三个区域,V1<-E,|V1|<E,V1>E,分别称为D-1,D0,和D1,如图3所示。
图3 蔡氏电路矢量场的三个区域
当 |V1|<E 时,对应区域蔡氏电路状态方程可表示为

式中,这个线性系统在原点处有一个单一的平衡点,其稳定性由
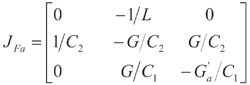 的特征值决
的特征值决定。其特征多项式为
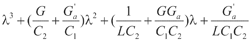 。设蔡氏电路各元件的参数为L=18mH C2=100nF,C1=10nF,G=1/R=550
。设蔡氏电路各元件的参数为L=18mH C2=100nF,C1=10nF,G=1/R=550 s,当G=1/R=550
s,当G=1/R=550 s时,蔡氏电路已处于混沌状态,可得的特征值为
s时,蔡氏电路已处于混沌状态,可得的特征值为 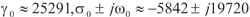
从而使D0相轨沿着区域中的不稳定实特征值r0相对应的特征矢量Er(0)的方位由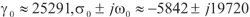 ,或者由
,或者由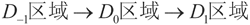 ,形成了蔡氏混沌吸引子的键波运动(及单向运动)。
,形成了蔡氏混沌吸引子的键波运动(及单向运动)。
当 |V1|>E 时,对应D0区域蔡氏电路状态方程可表示为

式中G'=G+Gb,I'=(Gb-Ga)E。当V1<-E时,对应D1区域,当V1>E时,对应D1区域,其平衡点分别为P-和P+,附近的稳定性可由

的特征值决定,其特征多项式为
 ,设电路的参数已如前所述,可得的特征值为
,设电路的参数已如前所述,可得的特征值为
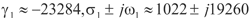
可知在D1和D-1区域中,实特征值在平衡点相对应的特征矢量分别为Er(P+)和Er(P-),而复共轭特征值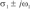 在平衡点相对应的特征矢量所构成的平面分别为Ec(P+)和Ec(P-),。由于r1<0,
在平衡点相对应的特征矢量所构成的平面分别为Ec(P+)和Ec(P-),。由于r1<0,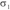 >0,故在D1和D-1区域分别形成了两个相对稳定的向外扩展的螺旋运动。
>0,故在D1和D-1区域分别形成了两个相对稳定的向外扩展的螺旋运动。
综上所述,蔡氏电路可产生一个双螺旋混沌吸引子,其相轨迹图和相对应的时域波形图及键波图分别如图4,图5,图6所示。
在D1区域或D-1区域中,可得:r1≈-23284,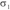 =1022 ,w1=19260。由此可得螺旋运动的基波分量的频率为
=1022 ,w1=19260。由此可得螺旋运动的基波分量的频率为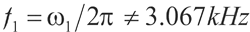 ,则高次谐波分量为mf1 (m=1,2,3……)
,则高次谐波分量为mf1 (m=1,2,3……)
图4 双涡卷混沌吸引子相图 图5 双涡卷混沌吸引子时域波形图

图6 混沌波形及其对应的键波4 基于chua电路键波同步系统的设计
本文设计了一个基于改进型Chua电路键波同步系统,实验电路如图 7 所示,图中Chua混沌电路的参数分别选为
图7 基于Chua电路的键波同步电路系统L=18mH,R=1.7
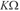 ,C1=10nF,C2=100nF。 为蔡氏二极管,它由双运放TL082组成,和6个电阻构成. 用双电源供电,其伏安特性为分段线性函数,其中中间段的斜率为Ga=-0.72ms,其余两段的斜率为Gb=-0.41ms,转 折 点 电 压 为E=1V。在图7所示的实验中,混沌同步的通道中串接了一个低通滤波器,其作用是滤除掉混沌信号的高频分量,而允许低频分量 (即键波分量)通过。实验测得,R0=0.5
,C1=10nF,C2=100nF。 为蔡氏二极管,它由双运放TL082组成,和6个电阻构成. 用双电源供电,其伏安特性为分段线性函数,其中中间段的斜率为Ga=-0.72ms,其余两段的斜率为Gb=-0.41ms,转 折 点 电 压 为E=1V。在图7所示的实验中,混沌同步的通道中串接了一个低通滤波器,其作用是滤除掉混沌信号的高频分量,而允许低频分量 (即键波分量)通过。实验测得,R0=0.5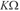 ,C≤0.1
,C≤0.1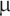 F时,收发混沌仍能保持较好的同步,由此可得其上限截止频率为
F时,收发混沌仍能保持较好的同步,由此可得其上限截止频率为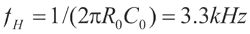 。
。
实验结果表明:
(1)只传送混沌同步信号的一分低频信息(即键波分量),仍能使收发混沌保持良好同步。
(2)混沌吸引子低频分量的传送对混沌信号步至关重要,它必须包含键波信号所产生的频谱特征频谱分量,才能保证收发混沌的同步。
(3)只传送键波产生的特征频谱分量,滤除涡卷产生的高频分量,混沌同步仍能保持,这不仅能满足在实际信道中传送同步信息的要求,还能提高混沌通信的保密性和信噪比。
(4)当驱动信号在传输过程中有衰减时,系统仍能很好同步。这个性质对实际系统是十分重要的。
(5)驱动响应系统的所有元器件参数相同,则不论两系统初始值如何,很快达到完全同步。当两系统的元器件参数有 5%以下误差时,同步性能仍很好,因此驱动响应式 Chua电路混沌同步具有一定的鲁棒性。
(6)键波产生的低频分量称之为特征频谱,它对同步至关重要。键波对外界信号(实际中表现为干扰和噪声)中的低频分量的干扰有较高的敏感性,对混沌的同步有很大的影响,而外界信号中的高频分量由于涡卷的高频基波相对稳定,对混沌的同步影响较小。
5 结束语
本文介绍了一种改进型Chua电路及其特性;分析了蔡氏电路中混沌吸引子的键波及螺旋表示方法;设计了一个基于Chua电路键波同步系统;通过实验给出了混沌系统同步与混沌吸引子键波之间的关系,为混沌同步系统在保密通信的实际应用奠定了一定的基础。此外,采用何种方法进行混沌键波的同步控制,如何在混沌同步键波控制信号有较大衰减情况下保证系统的同步?都是非常令人感兴趣并值得今后继续探讨研究的课题。
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



