- 软测量技术在大气环境质量评价上的应用
-
企业: 控制网 日期: 2007-09-26 领域: 工业以太网 点击数: 1457
关键词:大气环境质量评价;软测量;神经网络;倍斜率聚类法;等效数值法 余丙荣(1971-)
余丙荣(1971-)
男,安徽宿松人,工学学士、安徽大学电子与通信工程硕士生,研究方向为电力电子、控制理论。
1 引言
目前,环境污染已经成为了一个严峻的问题,特别是城市、工业区,环境污染甚是严重。大气污染也是环境污染问题的重要部分,现在几乎每个城市每天都要向环境部门报告其空气污染情况和空气污染指数,以确定该城市的工业生产和环境治理力度是否合格。所以对空气环境的质量评价即空气污染指数的计算是不可缺少的部分,不仅要求准确,而且还要快速。近年来,在环境质量综合评价方面已提出了很多评价模型,各有各的优缺点。本文将用神经网络的方法来对空气环境质量作评价,通过应用于大气环境质量评价的具体实例来与两个经典评价模型倍斜率聚类法、等效数值法作比较并分析其评价的结果。
2 软测量方法概述
软测量技术是通过选择一些容易测量且有关的变量(辅助变量),构造一个与输出建立联系的数学模型,且用计算机软件实现估计出输出变量(主导变量)的方法。建立软测量的方法有很多,在经验建模法中,介绍一下人工智能的方法——人工神经网络。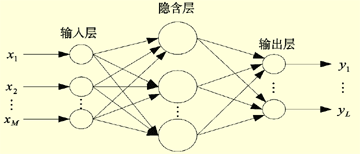
图1 径向基神经网络结构
2.1 RBF神经网络模型
RBF神经网络也叫径向基神经网络,它是一种局部逼近的神经网络。其结构由三层组成:输入层、隐含层和输出层,如图1所示,隐含层第i个节点的输出表示为:
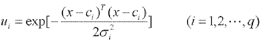 (1)
(1)
式中,ui是第个i节点的输出, 是第i个节点的标准化常数,q是隐含层的节点数,x=(x1,x2,...,xM)T是样本输入;Ci是第i个节点高斯函数的中心向量,此向量是一个与输入样本x的维数相同的列向量,即Ci=(Ci1,Ci2,...,CiM)T 由式(1)可知,节点的输出范围在0和1之间,且输入样本越靠近节点中心,输出值愈大。当x=Ci时, Ui=1。
是第i个节点的标准化常数,q是隐含层的节点数,x=(x1,x2,...,xM)T是样本输入;Ci是第i个节点高斯函数的中心向量,此向量是一个与输入样本x的维数相同的列向量,即Ci=(Ci1,Ci2,...,CiM)T 由式(1)可知,节点的输出范围在0和1之间,且输入样本越靠近节点中心,输出值愈大。当x=Ci时, Ui=1。
从隐含层到输出层即Ui(x)→yk为线性映射,表示式为:
 (2)
(2)
式中,ui是隐含层第i个节点的输出;yk是输出层第k个节点的输出;wki是隐含层到输出层的加权系数;θk是输出层的阈值;q是隐含层节点数。
2.2 RBF神经网络学习过程
设训练样本有N个,则系统的总误差表示式为:
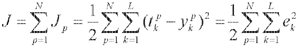 (3)
(3)
式中,N为模式样本对数;L为网络输出节点数; 表示在样本p的作用下的第k个神经元的期望输出;
表示在样本p的作用下的第k个神经元的期望输出; 表示在样本p的作用下的第k个神经元的实际输出。
表示在样本p的作用下的第k个神经元的实际输出。
其学习过程分为两个阶段:无教师学习阶段和有教师学习阶段。
2.2.1 无教师学习阶段
可以通过k-均值聚类算法来对所有样本输入进行聚类,求得各隐含层节点的RBF的中心向量,其算法如下:
(1)给定各隐节点初始中心向量Ci(0)和判定停止计算的;
(2)计算欧式距离,并求最小距离节点;
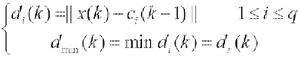 (4)
(4)
式中,k为样本序号,r为中心向量Ci(k-1)与输入样本x(k)距离最近的隐节点序号;
(3)调整中心向量
 (5)
(5)
式中,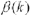 是学习速率。
是学习速率。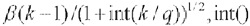 为取整运算。每经过q个样本之后,调小一次学习速率,逐渐减至零。
为取整运算。每经过q个样本之后,调小一次学习速率,逐渐减至零。
(4)判断聚类质量
 (6)
(6)
对于全部样本反复进行以上运算,直到以上条件或聚类结束。
2.2.2 有教师学习阶段
当Ci确定以后,求隐含层至输出层之间的权值Wki(k=1,2,...,L;i=1,2,...,q)就成了线性优化问题,其权值的学习算法为:
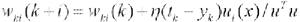 (7)
(7)
式中,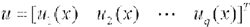 ,ui(x)为高斯函数;
,ui(x)为高斯函数;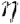 为学习速率,且0<
为学习速率,且0< 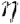 <1;tk和yk分别表示第k个输出分量的期望值和实际值。由于向量u只要少量几个元素为1,故需要调整量少,学习速度比较快。
<1;tk和yk分别表示第k个输出分量的期望值和实际值。由于向量u只要少量几个元素为1,故需要调整量少,学习速度比较快。
3 软测量技术在大气环境质量评价上的应用
表1和表2为国家大气环境质量分级标准(GB3095-1996)以及本文要用到的分级标准浓度限值。
表1 大气环境质量分级标准 (mg/m3)
污染物
Ⅰ
Ⅱ
Ⅲ
Ⅳ
SO2
0-0.05
0.05-0.15
0.15-0.25
0.25-∞
NOx
0-0.10
0 -0.10
0.10-0.15
0.15-∞
TSP
0-0.12
0.12 -0.30
0.30-0.50
0.50- ∞
表2 分级标准浓度限值 (mg/m3)
分级
SO2
NOx
TSP
Ⅱ
0.15
0.10
0.12
Ⅱ
0.15
0.10
0.30
Ⅳ
0.25
0.15
0.50
这里假设环境质量标准为连续的数,表2表示当污染物开始达到限度值时,分级标准开始达到标准值。分级指标=(int)环境质量标准,即取整。下面以各污染物浓度作为该软测量技术方法的辅助变量,以分级标准作为主导变量通过MATLAB软件来建立评价模型,各设计参数取默认值,其结果如图2所示。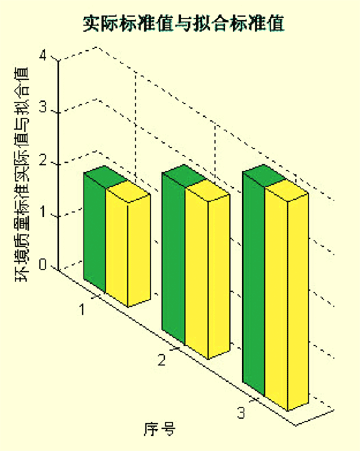
图2 环境质量模型的拟合评价效果其输出层网络训练的误差曲面如图3所示。

图3 训练误差曲面图表3为某市大气污染指标实测值。
表3 某市大气污染指标实测值
监测点
A1
A2
A3
A4
A5
A6
A 7
A8
A9
A10
SO2
0.125
0.022
0.131
0.097
0.067
0.014
0.176
0.029
0.1
0.038
NOx
0.086
0.013
0.016
0.027
0.035
0.018
0.123
0.026
0.075
0.038
TSP
0.239
0.188
0.101
0.417
0.657
0.409
0.415
0.274
0.225
0.462
根据上面已建立好的评价模型,对此市大气污染指标进行评价,并与倍斜率聚类法、等效数值法列表作比较,其结果如表4所示。
表4 各软测量方法的结果比较
监测点
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
评价数值结果
2.6702
2.1333
1.9955
3.2580
3.9199
3.0081
3.5391
2.5266
2.5428
3.2877
评价数值指标
Ⅱ
Ⅱ
Ⅰ
Ⅲ
Ⅲ
Ⅲ
Ⅲ
Ⅱ
Ⅱ
Ⅲ
倍余率聚类法
Ⅱ
Ⅱ
Ⅱ
Ⅱ
Ⅲ
Ⅱ
Ⅲ
Ⅱ
Ⅱ
Ⅱ
等效数值法
Ⅱ
Ⅱ
Ⅱ
Ⅲ
Ⅲ
Ⅲ
Ⅲ
Ⅱ
Ⅱ
Ⅲ
从表4可以看出,用软测量技术的神经网络技术作评价,其结果与倍斜率聚类法、等效数值法的结果基本上一致,特别是与等效数值法,基本一样。从计算过程来看,软测量技术计算非常简捷,只需要输入数据,通过计算机软件,立即得到结果,并从数据中可以看出其偏向前一级或后一级的趋向。而倍斜率聚类法等中隶属函数的建立以及计算相对复杂。
根据神经网络这一软测量方法所建立的评价模型,可以确定其辅助变量与主导变量的关系,即y=f(x), x=[x1,x2,...,xp]T 为辅助变量,y=[y1,y2,...,yt]T为主导变量。本例中它们之间的函数关系为:tx=simurb(px,w1,b1,w2,b2),px为辅助变量,tx为主导变量。
4 结束语
用神经网络的软测量方法对大气环境质量评价,因为要经过多次训练,其评价误差可达到很小,本例为10-16以下,而且通过神经网络的方法,可以很方便地得到输入与输出的函数关系。使用方便,在环境评价中的应用前景广阔。参考文献:
[1] 李泽应,曹菁菁等. RBF 神经网络及其在水质评价中的应用.兵工自动化,2006.7.
[2] 阮沈勇,王永利. MATLAB程序设计.北京:电子工业出版社,2004.1.
[3] 李国勇.智能控制及其MATLAB实现.北京:电子工业出版社,2005.5.
[4] 乔敬萍.几种环境质量评价方法的应用.山西大学学报(自然科学版),2004.
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



