- 基于霍夫变换和几何特性的图像识别方法
-
企业: 控制网 日期: 2007-09-29 领域: SCADA-RTU 点击数: 4675
关键词: 霍夫变换;图像识别;自动报靶 顾筠(1963—)
顾筠(1963—)
女,陕西西安人.江苏广播电视大学信息工程系讲师。
1 引言
在计算机视觉领域中,如何从当前的图像中提取所需要的特征信息是图像识别的关键所在。在许多应用场合中需要快速准确地检测出圆或椭圆,从而进行更深一步的操作,例如在基于图像处理的自动报靶系统中,对靶环的识别就属于这样的一类应用。在这方面很多学者提出了各种方法,如文献[1]中提出了采用规则三角形网格的控制点校正方法,文献[2]中提出了加入方向图滤波的方法,对低成本普通摄像头的几何失真(“桶形”、“枕形”或者其他不规则的变形)进行校正,取得了一定的效果。在笔者研究的自动报靶系统中,图像采集部分用的是高精度的摄像头,这样,传统意义上的几何失真并不明显。影响报靶精度的主要矛盾之一,是由于摄像头与靶纸之间的不完全垂直而引起的线性变形。
摄像头采集到的图形是椭圆或者是圆,如果能够得到椭圆/圆的各个参数再加上对弹孔的定位,就可以根据公式计算出环值。本文提出了利用椭圆的几何特性和边缘方向信息将参数空间分解,用多级低维的霍夫变换来实现椭圆的检测,大大减小了计算量和内存占用量,满足了对靶环识别的应用需求。
2 霍夫变换及椭圆/圆的几何特性引理
2.1 霍夫变换原理
霍夫变换用于直线检测的基本策略为:由图像空间的边缘点去计算参数空间中参考点的可能轨迹,在累加器中给计算出的参考点计数, 最后选出峰值。 因为它将直角坐标系中的线变为极坐标中的点,故一般常将霍夫变换称为线、点变换。 如图1中的直线可用参数表示为:
ρxcos (θ)+y sin (θ)
其中:λ为图象空间中的某条直线;P为原点到λ的垂直距离;α为λ斜率角度;λ在ρ-θ平面上可表示为一点(P ,α)。
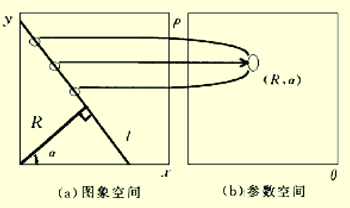
图1 直线的霍夫变换根据这个原理,可以用霍夫变换提取直线,通常将x-y平面称为图像平面,ρ-θ平面称为参数平面。 将该思想推广到检测曲线,则称为广义霍夫变换。
2.2 椭圆/圆的几何特性引理
引理1:设E为一椭圆或圆,现对自左向右,自上而下扫描,假设每一水平扫描线λHi与相交于点XL i和XR i,XM i为XL i和XR i的中点,则所有XM i均处于同一条直线lV上,称其为纵轴,XL i(XR i)则称为XR i(XL i)对于lV的对称点(见图2)。
引理2:设E为一椭圆或圆,现对E自上而下,自左向右扫描,假设每一垂直扫描线lV i与E相交于点 YT i 和YR i,YM为YT i 和YR i的中点,则所有 YM均处于同一条直线lH上,称其为横轴,YT i(YR i)则称为YR i(YT i)对于lH的对称点(见图2)。
引理3:设为一椭圆或圆,lV和lH为E的两条对称轴,则lV和lH的交点即为椭圆E的中心O(见图3)。
以上引理的证明可参见文献[6,7]。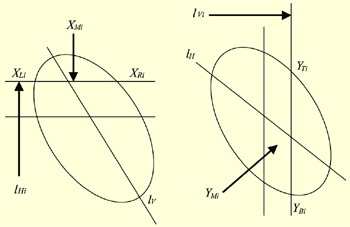
图2 纵轴lV 与 横轴lH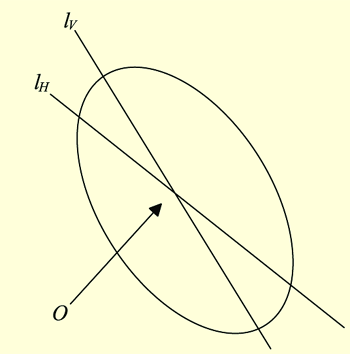
图3 获得椭圆圆心3 应用实例
霍夫变换是检测椭圆的有效方法,若将标准霍夫(SHT)或者广义霍夫变换(GHT)直接用于椭圆检测,由于椭圆有5个自由参数,需要在五维参数空间进行累积,致使这种算法因计算量和内存需求量过大而难以在实际中应用。为了克服上述缺陷,Xu[3]等提出了随机霍夫变换(RHT),在图像空间随机地选取不在一条直线上的几个点映射成参数空间的一个点,是多到一的映射。从而避免了霍夫变换一到多映射的巨大计算量。但在处理复杂图像时,由于无目标的随机采样会引入大量的无效采样与无效累积,使计算性能大大降低。笔者提出了利用椭圆的几何特性和边缘方向信息将参数空间分解,用多级低维的霍夫变换来实现椭圆的检测,大大减小了计算量和内存需求。
3.1 形心的提取
在靶环识别的过程中,最关键的一步就是对形心的提取,只有快速精确地得到形心才能更好的进行后续的各项操作。在开始提取椭圆形心前,首先对图像进行预处理,包括灰度化、二值化、低通滤波等,并将得到的图像存在图像C中。此时,图像C中含有数个同心椭圆(包括一些噪声点)。图4(a)为原始图像,图4(b)为经过预处理的。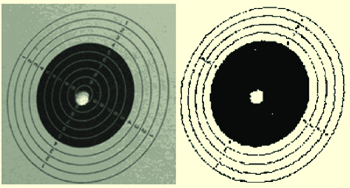
(a)预处理前 (b)预处理后
图4 预处理前后的图像形心坐标的提取步骤如下:
(1) 从第一行开始自左向右扫描图像C,如果扫描到的数值是0(二值化后0表示黑色象素,1表示白色象素),则保存该点的坐标,并且再自右向左扫描这一行寻找黑色象素,保存其坐标。这样扫描完整张图就可以得到外圈的椭圆边界。初始化一空白图像D,对于每个边界特征点,应用引理1,求得所有的XM i,并将其存于D中。
假设XM i所在直线的方程在极坐标内可表示为:ρ=xcos(θ)+ysin(θ)。考虑一个以参数ρ和θ定义的二维空间,x-y平面的任意一直线对应了该空间的一个点。因此,x-y平面的任意一直线的霍夫变换是ρ-θ空间的一个点。现在考虑x-y平面的一个特定的点XM i,坐标为(x,y),过该点的直线可以有很多,每一条都对应了ρ-θ空间中的一个点。然而这些点必须是满足以x和y作为常量时的等式。因此在参数空间中与x-y空间中所有这些直线对应点的轨迹是一条正弦曲线,而x-y平面上的一个点(图5(a))对应了ρ-θ空间的一条正弦曲线(图5(b))。这一组XM i中绝大多数都是位于由参数ρ0和θ0决定的直线上的边缘点,所以这些边缘点对应于ρ-θ 空间的正弦曲线中绝大多数都交于点(ρ0, θ0),因为这是它们共享的一条直线的参数 。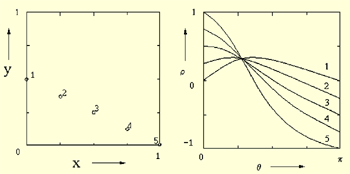
(a) x-y空间 (b) ρ-θ 空间
图5 x-y空间与ρ-θ空间的对应关系为了找出这些点所构成的直线段,我们可以将ρ,θ空间量化成许多网格。根据每一个XM i点的坐标(x,y)代入θ的量化值,算出各个ρ ,所得值(经量化)落在某个网格内,便使该网格的计数累加器加1,等全部(x,y)点变换后,对网格进行检测。计数值大的网格对应于共线点,其(ρ,θ)可用作直线拟合参数,据此得到lV(如图6,为了能看得清楚,图中的黑色区域已去除)。
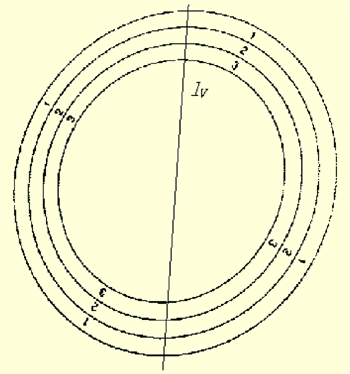
图 6 提取得到的lV(2) 重新初始化D,自上向下扫描C,对于每个边界点,应用引理2,求得所有的YM i,并将其存于D中。对图像D作如上所述的变换检测直线,检测到的结果即是lH。求lV和lH的交点,根据引理3,该交点即是图像中外圈椭圆的形心。如图7,两直线的交点即是所要提取的靶心。所示位图的大小为340×369像素,以左下角第一个像素点为坐标原点(0,0),则辨识到的形心坐标为(167,187)。
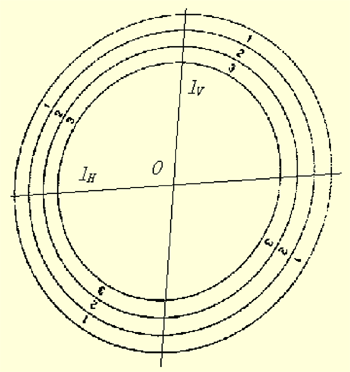
图 7 提取到的lH,交点O为靶心3.2 椭圆旋转角的获取
当椭圆以(x0,y0)为圆心,旋转角为0时,P(xp,yp)满足以下关系:
设P(xP,yP)为椭圆上某一点,P为P点梯度,a和b分别为椭圆的半长轴和半短轴。对于圆心在(x0,y0)、旋转角度为0的椭圆,P(xP,yP)满足以下关系:
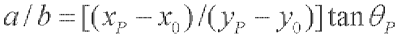 (1)
(1)
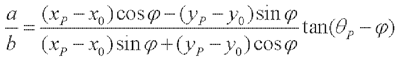 (2)
(2)
由式(2)可知,目前的未知参数为长短轴比a / b和旋转角?(0 < φ<2π),令h = a/b,利用霍夫变换在(h,φ)空间上投票,并在(h,φ)空间上找到局部最大值,从而确定h和φ的值。经过对上图的运算得到结果为h=1.136,φ=63.435 o。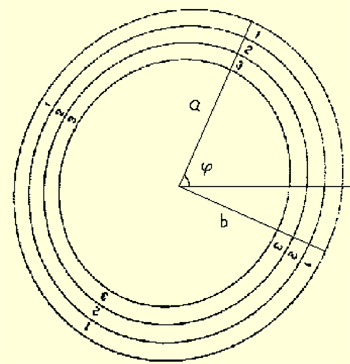
图8 a、b和φ
3.3 椭圆长短轴的确定
在h = a / b已知的条件下,椭圆上点P(xp,yp)满足下式:
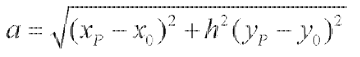 (3)
(3)
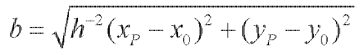 (4)
(4)
如果在2.2中成功获得了h = a / b的值,则椭圆的长短轴值可由(3、4)式求得。上图的运算结果为a=179.4,
b=157.7。
4 实验结果
采用以上算法能够快速准确地的获取得图像中所需图形的几何参数。算法是用vc++语言[5]实现的 ,在Pentium 42.4GHz的机器上检测形心的运算时间小于0.1秒;对一幅340×369的位图,形心的定位误差小于2个像素点。这样的运算速度和检测精度完全能够适应自动报靶系统的实时性、准确性要求。
5 结束语
本文讨论了利用几何特性提取图像中图形的几何参数的方法,并根据对称性特点快速确定形心,滤除原图中不必要的干扰信息,降低了霍夫变换参数空间的维数,达到了准确、快速提取几何参数的效果。在实际应用过程中,参数空间中累加器的叠加及寻找局部最大值时的阈值的选取尤为重要。本文的实现过程中,参数空间阈值的选取仍依靠经验来选取某一固定值,这有待今后进一步研究。由于算法中采用霍夫变换的投票机制确定参数,使得图像中图形边界即使不连续或者部分残缺(<30%)的情况下,仍能达到较为满意的结果。参考文献:
[1] 鹿洪旭,卢朝阳,高西全等.用于射击运动自动判靶的图像校正算法及其实现[J].计算机工程与科学,2001,23(3):21~24.
[2] 张建波,高西全,丁玉美等.一种提高射击运动自动判靶系统精度的方法[J]. 计算机工程与科学,2002,29(3):324~327、342.
[3] Xu L, O ja E . Randomized Hough transform (RHT) : basic mechanisms,algorithms and computational complexities[J],Computer Vision Graphic Image Process : Image understanding , 1993,57 (2) : 131-154.
[4]彭扬,胡福桥,李介谷.椭圆特征的快速提取,上海交通大学学报,1998, 32(9) :61-63.
[5] 何斌,马天予,王运坚.《Visual C++ 数字图像处理》,北京:人民邮电出版社,2001.
[6] Huang C L . Elliptical feature extraction via an improved hough transform . Pattern Recognition Letters , 1989,10 : 93-100.
[7] Ho Chun Ta , Chen Ling Hwei . A fast ellipse/circle detector using geometric symmetry . Pattern Recognition , 1995,28 : 117-124.
作者信息:
顾 筠(江苏广播电视大学信息工程学院,江苏 南京 210036)
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



