- 参数自调整模糊控制器研究及基于FPGA实现设计
-
企业: 控制网 日期: 2008-03-02 领域: 人机界面 点击数: 1197  路永坤(1976-)
路永坤(1976-)
男,硕士,讲师,(天津科技大学电子信息与自动化学院,天津 300222),主要从事电子技术的有关教学工作、以及控制理论与应用、电子技术应用、信息管理系统等方面的研究工作。
摘要:给出参数自调整模糊控制器的原理。利用MATLAB,分析了一种参数自调整模糊控制器的控制效果。分析了各种模糊控制器的实现方案。同时给出目前FPGA的发展状况,并且分析了相应工业控制应用情况。最后,给出了基于FPGA的参数自调整模糊控制器的实现结构。
关键词:参数自调整;模糊控制器;MATLAB;实现方案;FPGA;实现结构Abstract: In this paper, the principle of parametric self-tuning fuzzy controller is given. Its control effect is analyzed by using MATLAB. Implementation schemes are analyzed with various fuzzy controllers. Meanwhile the development situation of FPGA is given, and its application in industrial control is analyzed. Finally, the Implementation structure of parametric self-tuning fuzzy controller is given based on FPGA.
Key words: parametric self-tuning fuzzy controller;MATLAB;Implementation scheme;FPGA;Implementation structure
1 引言
由于模糊控制不依赖系统的精确模型,具有一定适应能力、鲁棒性好等特点,所以模糊控制器在工业控制系统中有着广泛的应用场合。传统模糊控制器对特定专家的经验依赖大,所以有关模糊控制器的性能优化是人们一直以来关注的问题。其中,参数自调整模糊控制器就是一种基于对模糊控制器的输入和输出的量化因子进行自动调节的改进模糊控制器。
有关模糊控制器的成功实现方案很多,例如基于PC机或单片机等。近年随着电子集成制造工艺以及计算机辅助设计技术的发展,出现了基于EDA工程[1] 的FPGA开发技术。利用FPGA丰富的硬件资源,以及方便的辅助开发工具,可以开发一些新型的自动化控制器。
本文给出一种具有一定适应能力的参数自调整模糊控制器,并且给出有关基于FPGA的实现设计方案。
2 参数自调整模糊控制器原理与设计
2.1 模糊控制器原理
普通的模糊控制器包括模糊量化、模糊规则、模糊决策、模糊判决等五个大部分。其中,模糊量化完成对输入精确量转换为输入模糊量。模糊规则是一系列控制规则,通常是一组IF-THEN结构的规则。模糊决策是根据输入模糊量以及模糊控制规则,获得有关模糊决策值。模糊判决是指从决策值模糊集中,判决出一个确切的清晰量。然后把有关控制量作用到被控制对象上。通常在模糊量化的过程中,对输入量要乘以一个比例因子,进而量化到模糊区间上。相类似,在模糊判决输出的决策模糊量也要乘以一个比例因子,进而量化到控制量的精确区间上。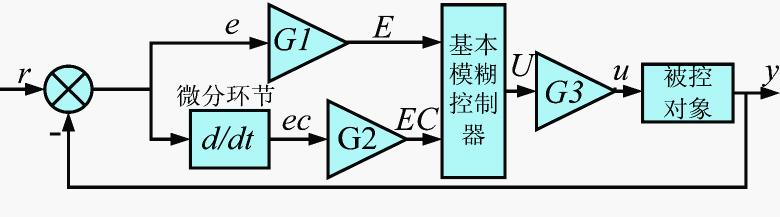
图1 普通模糊系统的原理示意图图1是普通模糊系统的原理示意图。图中,r、y、e和ec分别是系统的输入信号、输出信号、系统的误差信号、系统输入误差微分信号。E和EC分别是,系统输入误差信号以及相应误差微分信号,量化到模糊区间上的对应量化值。U是模糊判决控制的决策模糊量,u是控制量化值转换到控制精确区间的对应输出控制量。G1、G2、G3分别为输入量化以及控制量化的比例因子。
比例因子G1、G2和G3对系统响应的影响很大。若G1变化时候,则控制决策表相应的水平覆盖域发生变化,使同一数量值的e所处的水平区域发生变化,相应的输出控制量便可能发生变化。实践证明:在系统响应曲线的上升段,G1的变化将影响系统响应速度,G1越小,死区越小,响应越快,但超调量也越大;在稳定段,也就是E和EC都处在相应零位置的时候,系统的稳态误差与量化因子G1大小成反比。若G2变化,同理也会影响ec所处的水平区域发生变化,相应的输出控制量便可能发生变化。实践证明:对G2的变化,在设定点附近尤其敏感,当G2变小时,控制灵敏度增加,但也增加了收敛的困难,失去了一部分控制规则;而当G2变大时,控制器反应迟钝,容易造成振荡。G3直接影响模糊控制器的输出。在初始段,控制器若以绝对量输出时,G3对控制没什么影响;但当控制器以增量形式输出时,若工作在正值区,G3的增大使输出量也相应增大,上升变快,死区变小;但在收敛段,控制器工作在负值区,G3增大将导致输出量大幅度减少,使得系统缓慢逼近设定值,特别在稳定段,G3大会引起振荡[2]。
由G1、G2、G3对系统响应的影响,可知在不同阶段对有关比例因子分段取值,显然可以提高模糊控制的控制效果。所以,在本改进的模糊控制器中,采用了对有关比例因子进行调整的策略,也就是所谓的参数自调整模糊控制器。
2.2 自调整模糊控制器
文献[3] 所提出的自调整模糊控制器,就是采用了在控制中根据输入量误差的大小不同,对有关比例因子进行动态改变。从而提高了有关控制效果。
图2 自调整模糊控制系统的系统仿真模型框图图2为有关自调整模糊控制系统的系统仿真模型框图。图2中,subsystem部分为封装的参数调整模块,由S函数实现。其实,这种控制器的设计结构具有一定普遍意义,对模型参数在一定范围内的变化也有适应性。图3是利用MATLAB[4]对有关自调整模糊控制系统进行仿真的对比结果。A曲线是在被控对象模型为
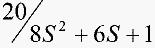 时,采用普通模糊控制器,固定比例因子的仿真曲线。B曲线是在被控对象模型为
时,采用普通模糊控制器,固定比例因子的仿真曲线。B曲线是在被控对象模型为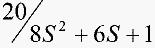 时,采用参数自调整模糊控制器的仿真曲线。C曲线是在被控对象模型参数变为
时,采用参数自调整模糊控制器的仿真曲线。C曲线是在被控对象模型参数变为 时,采用参数自调整模糊控制器的仿真曲线。由图3说明,对于同一个控制对象,采用参数自调整控制器效果要明显优于普通模糊控制器。并且,当对象模型参数发生变化时,系统仍然具有适应性。
时,采用参数自调整模糊控制器的仿真曲线。由图3说明,对于同一个控制对象,采用参数自调整控制器效果要明显优于普通模糊控制器。并且,当对象模型参数发生变化时,系统仍然具有适应性。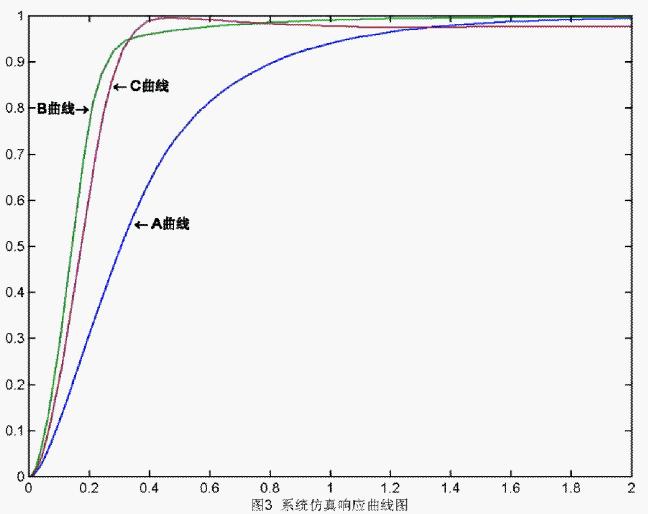
图3 系统仿真响应曲线图3 基于FPGA的参数自调整模糊控制器设计
在模糊控制理论被实际应用后,模糊控制器的硬件化实现已经取得了很大的成果。一般是用单片机、PC机或者DSP芯片以及相应控制电路来实现。但功能日益完善的FPGA相对于单片机与DSP有很大的优势。
用户可对FPGA内部的逻辑模块和I/O模块重新配置,以实现用户的逻辑。它还具有静态可重复编程和动态在系统重构的特性,使得硬件的功能可以像软件一样通过编程来修改。工程师可以通过传统的原理图输入法,或是硬件描述语言自行设计一个基于FPGA的数字系统。通过软件仿真,我们可以事先验证设计的正确性。在PCB完成以后,还可以利用FPGA的在线修改能力,随时修改设计而不必改动硬件电路。使用FPGA来开发数字电路,可以大大缩短设计时间,减少PCB面积,提高系统的可靠性。
不过早期限于开发工具与工艺的限制,很多模糊控制系统的芯片化实现是由微电子或者相近专业的研究人员来完成的[5]。但限于专业的差异,很多具体领域的基于FPGA为基础的模糊控制芯片开发不多。不过近几年,随着计算机辅助工具的发展,出现了EDA工程[1]。有关FPGA的设计开发工具也被普遍推广,所以在自动化领域,越来越多的基于FPGA的控制器[6]涌现出来。
但是在仅仅以FPGA为基础的方案实现里,很多有关数据运算过程的实现过程复杂。不过,由于FPGA所固有的并行处理结构,因此在进行复杂计算时性能远远超过传统DSP处理器。所以如果设计合理,一般用FPGA开发的专用模块的计算速度快于一些传统DSP以及其他微处理器[7]。
如果选用具有已经内置DSP硬件资源的FPGA,那么在设计结构上会更合理一些。但一般来说,对于开发有DSP资源的FPGA,不管从芯片还是开发工具上,成本都很昂贵。不过,目前出现一些低成本的内置DSP的FPGA。对于FPGA的两大主要生产商Xilinx公司与Altera公司,它们提供低成本的DSP与FPGA优势互补的芯片,目前分别为Spartan-3与Cyclone III。这些芯片目前在通讯领域应用比较多,但对于工业自动化系统的实现来说应用不多。所以,参数自调整模糊控制器的实现,可以采用这种低成本具有DSP的FPGA芯片为硬件基础。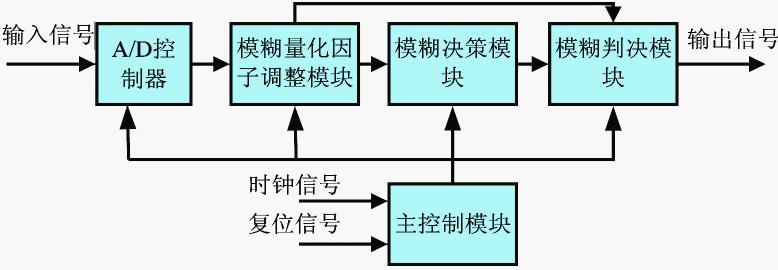
图4 是模糊控制器实现结构示意图其中,A/D控制器部分,实现对A/D转换控制器的有关控制。模糊量化因子调整模块部分,实现根据系统误差大小,合理选择量化调节的比例因子的作用。模糊决策模块根据模糊规则与输入模糊量进行模糊推理,得到模糊化的控制量化值。模糊判决模块把有关模糊决策的控制量化值转换为具体控制量,当然其中包括模糊输出的量化因子部分。其中,主控制模块的作用为协调各个模块之间的工作,具体为向每个模块提供时钟信号、复位信号、以及各个模块的起/停信号。
4 结束语
参数自调整模糊控制器,通过动态调节模糊量化过程中的比例因子,来达到提高模糊控制器性能的效果。有关控制思路清晰、便于系统实现。并且所分析的参数自调整模糊控制器对不同环境的控制系统有一定适应性。最后给出了有关该模糊控制器的实现方案。对类似控制系统的实现有一定借鉴意义。参考文献
[1] 黄继业,潘松.EDA技术实用教程(第2版)[M].北京:科学出版社,2005.
[2] 韩启纲.模糊控制原理、设计及应用 第7讲高级模糊控制器的设计[J].冶金自动化,1996, No.1 : 51-52.
[3] 李祖欣. MATLAB在模糊控制系统设计和仿真的应用[J] .系统仿真学报, 2003, Vol.15 No.1: 132-134.
[4] 吴晓莉,林哲辉.MATLAB辅助模糊系统设计[M] . 西安:西安电子科技大学出版社,2002.
[5] 袁欣,干萌,蓝鸿翔等.模糊控制器专用集成电路的设计与实现[J] . 微电子学, 1996, Vol.26,No.1: .24-28.
[6] 林平. 变频控制系统集成模块及其控制芯片技术的研究[D] . 浙江: 浙江大学, 2003.
[7] 贺今朝. 一种基于FPGA的模糊控制器的研究[D] . 大连: 大连理工大学, 2002.
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



