- 基于BP网络的智能灰色预测在时滞系统中的应用
-
企业: 控制网 日期: 2008-04-12 领域: PLC&PAC 点击数: 1580  霍浩(1983-)
霍浩(1983-)
男,河北邢台人,硕士研究生,研究方向为过程控制算法的研究。
基金项目:四川省教育厅重点项目(2004A134)
摘要:基于灰色理论与神经网络相结合能改进预测精度的思想,本文将神经网络与灰色预测PID控制器相结合,利用神经网络来在线调节PID控制器参数以适应模型时变的要求。论述了其原理并将其应用于实际双容水箱液位控制系统,以克服模型不确定性带来的不利影响,从而实现对二阶液位对象的有效控制。通过MATLAB进行了算法的验证和仿真,并利用xPC技术进行了实时控制,结果表明此改进算法比常规PID控制具有更好的效果。
关键词:双容水箱;BP神经网络;灰色理论;PID;MATLAB/xPCAbstract: In this paper, based on the idea that the combination of grey theory and neural network can improve the forecasting precision of system, by integrating neural network and grey forecast PID controller,, we use the BP neural network to regulate online PID controller model parameters to adapt the changing requirements. In order to overcome model adverse effects of changes so that we can control effectively the second-order level system, we analyze the principles of the algorithm and apply it in the two-tank water control system, The algorithm is simulated by Matlab and xPC technology, and the result shows that the improved algorithm is more effective on improving parameter forecasting precision than the previous single PID algorithm.
Key words: Two-tank water system;neural network;grey theory;PID; MATLAB/xPC
1 引言
预测控制是当前研究的热点之一。而灰色预测控制方法不需要预先掌握对象的数学模型,而是实时在线建模。其数列预测不仅可以做“近期”预测,而且也适合于做“长期”预测,这对克服时滞系统带来的不利影响是非常合适的。灰色预测控制是将控制理论与灰色系统理论相结合的一种新型控制方法。灰色预测是用灰色模型(GM)进行的定量预测,灰色控制是对本征特性灰色系统的控制,或系统中含灰参数的控制,或用GM构成的预测控制,灰色系统理论是处理不确定量的一种有效途径[1]。
由于不确定部分对控制的影响不能忽略,使针对系统模型的PID控制器难于适应各种不确定性。许多学者提出对不确定部分建立灰色预测模型,在有限步数后,根据参数对不确定部分进行一定的补偿,以减小其影响,已取得了一定的控制效果,但控制精度还不是很高。由于BP神经网络具有在线快速学习的能力,有逼近线性或非线性函数的优良特性,与灰色预测相比,神经网络预测精度较高,且误差可控。为此,本文提出BP网络的智能灰色预测,对不确定部分建立BP神经网络的灰色预估模型,结合PID控制,使灰色PID控制器在线进行灰色预测和控制。灰色预估模型可根据系统的参数变化来自动调节预测补偿值,对系统响应具有适应性,从而获得更好的控制性能。
2 BP神经网络的自适应灰色预测PID控制器设计
PID控制要取得较好的控制效果,就必须通过调整好比例、积分和微分三种控制作用,形成控制量中既相互配合又相互制约的关系[2],这种关系不一定是简单的“线性组合”,而是从变化无穷的非线性组合中可以找出最佳的关系。神经网络所具有的任意非线性表达能力,可以通过对系统性能的学习来实现具有最佳组合的PID控制,采用BP网络,可以建立PID控制的三个参数kp、ki、kd自学习的PID控制器。基于BP网络的灰色预测PID控制系统结构如图1所示[3]。
控制器由三部分组成:
(1) 经典的PID控制器:直接对被控对象过程进行闭环控制,并且三个参数kp、ki、kd为在线整定方式;
(2) 灰色预测部分;
(3) 神经网络NN部分:网络输出层神经元的输出状态对应于PID的三个可调参数kp、ki、kd进行自适应调整,适应模型时变的要求。
采用神经网络BP算法作为控制器,就不必随着被控对象的模型参数的变化而变化控制器的参数,而是将被控对象的输出与给定值间的偏差信号作BP算法的输入数据,由BP算法根据自学习的结果,得出输出信号去控制实际对象,从而实现自适应控制。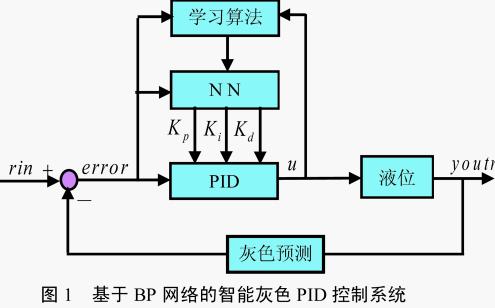
经典增量式数字PID的控制算法为:
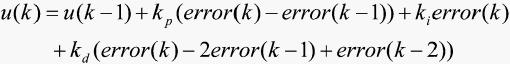 (1)
(1)
式中,kp、ki、kd分别为比例、积分、微分系数。
采用三层BP网络,其结构如图2所示,网络输入层的输入为式中,输入变量的
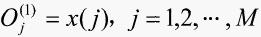 (2)
(2)
个数取决于被控系统的复杂程度。网络隐含层的输入、输出为
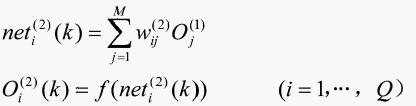 (3)
(3)
式中,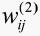 :隐含层加权系数;上角标(1)、(2)、(3)分别代表输入层、隐含层和输出层。
:隐含层加权系数;上角标(1)、(2)、(3)分别代表输入层、隐含层和输出层。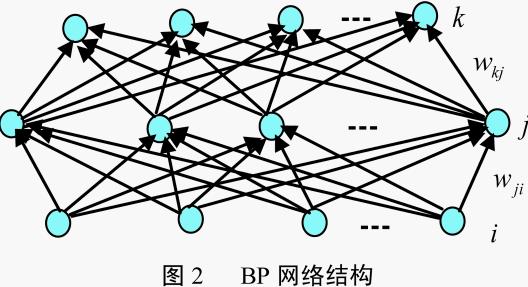
隐含层神经元的激励函数取正负对称的Sigmoid函数。
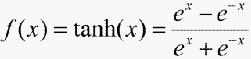 (4)
(4)
网络输出层的输入输出为
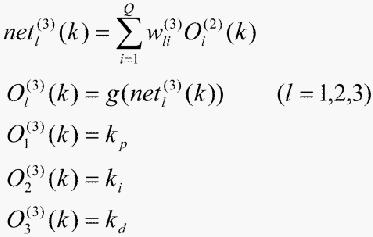 (5)
(5)
输出层输出节点分别对应三个可调参数kp、ki、kd。由于kp、ki、kd不能为负值,所以这里输出层神经元的活化函数取非负的Sigmoid函数:
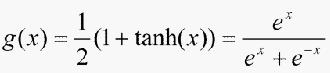 (6)
(6)
取性能指标函数为
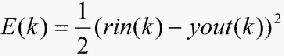 (7)
(7)
按照梯度下降法修正网络的权系数,即按E(k)对加权系数的负梯度方向搜索调整,并附加一个使搜索快速收敛全局极小的惯性项
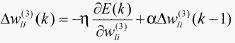 (8)
(8)
式中,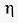 为学习速率;
为学习速率; 为惯性系数。
为惯性系数。
 (9)
(9)
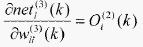 (10)
(10)
由于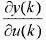 未知,所以近似用符合函数sgn
未知,所以近似用符合函数sgn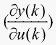 取代,由此带来计算不精确的影响可以通过调整学习速率
取代,由此带来计算不精确的影响可以通过调整学习速率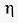 来补偿。
来补偿。
由公式(6)和公式(10),可求得
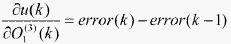 (11)
(11)
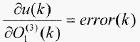 (12)
(12)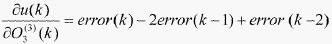 (13)
(13)
上述分析可得网络输出层权的学习算法为
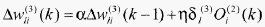 (14)
(14)
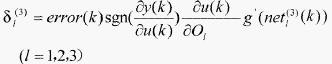 (15)
(15)
同理可得隐含层加权系数的学习算法。式中: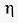 为动量系数,
为动量系数, 值越大则权系数调整的惯性越大,使调节尽快脱离饱和区。
值越大则权系数调整的惯性越大,使调节尽快脱离饱和区。
 (16)
(16)
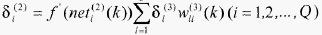 (17)
(17)
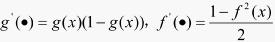 (18)
(18)
基于BP网络的自适应灰色预测PID控制器结构如图1所示,该控制器控制算法归纳如下:
注意:网络的输入:由于S型非线性函数F(x)随着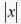 的增大,梯度下降,并趋于0,不利于权值的调整。因此,希望
的增大,梯度下降,并趋于0,不利于权值的调整。因此,希望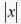 工作在较小的区域,故网络的输入要予以考虑,即若实际问题给以网络的输入量大于1,需作归一化处理。
工作在较小的区域,故网络的输入要予以考虑,即若实际问题给以网络的输入量大于1,需作归一化处理。
首先以各工况的最优PID参数作为BP神经网络的训练样本,离线学习NN,得到各层加权系数的初值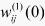 和
和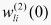 ,根据离线学习的信息,转入对被控对象实施控制,同时在线自学习。
,根据离线学习的信息,转入对被控对象实施控制,同时在线自学习。
(1) BP神经网络初始化:确定BP网络的结构,即确定输入层节点数M和隐含层节点数Q,并给出各层加权系数的初值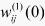 和
和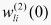 ,选定学习速率
,选定学习速率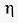 和惯性系数
和惯性系数 ,此时k=1;
,此时k=1;
(2) 采样得到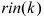 和
和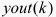 ,计算该时刻误差
,计算该时刻误差
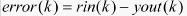
(3) BP网络的输入量进行归一化处理;
(4) 计算神经网络NN各层神经元的输入、输出,NN输出层的输出即为PID控制器的三个可调参数kp、ki、kd;
(5) 由公式计算(6)PID控制器的输出u(k);
(6) 进行神经网络学习,在线调整加权系数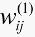 (k)和
(k)和 (k),实现PID控制参数的自适应调整;
(k),实现PID控制参数的自适应调整;
(7) 置k=k+1,返回到(1)。
3 仿真实验
3.1 MATLAB进行算法的验证和仿真
因大时滞的存在,给对象施加一个控制量后,要经过一个较长的滞后时间才能看到控制的效果,从而产生明显的超调,使得系统的稳定性变差,调节时间延长,控制难度加大。而液位系统是工业过程控制中较常见的单容自衡对象,是一种典型的纯滞后对象。本文采用双容水箱作为被控对象取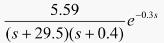 ,这里以液位模型滞后时间增大(即模型的滞后时间由0.3~0.35min变化,可写成0.3+0.05×(1-exp(-0.02×k))的形式)的情况,神经网络采用4-5-3的结构。经过反复的仿真与对比,在这里取定值R=1,数据采样间隔Ts=0.01min,建模维数m=5,预测步数k1=8,仿真结果如图3所示。
,这里以液位模型滞后时间增大(即模型的滞后时间由0.3~0.35min变化,可写成0.3+0.05×(1-exp(-0.02×k))的形式)的情况,神经网络采用4-5-3的结构。经过反复的仿真与对比,在这里取定值R=1,数据采样间隔Ts=0.01min,建模维数m=5,预测步数k1=8,仿真结果如图3所示。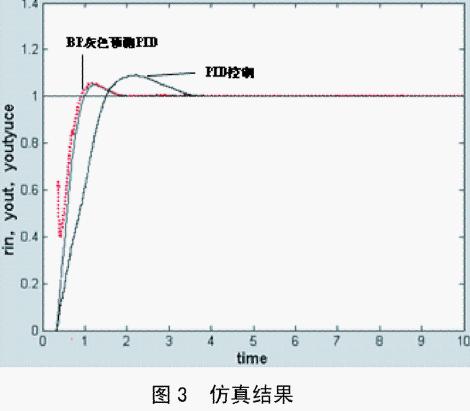
从图中可以看出,在对象参数发生变化后,本文所提出的控制策略具有明显的优越性。该方法的控制效果优于常规的PID控制,通过BP神经网络不断地在线调整kp、ki、kd三个参数,克服模型时变带来的不利影响,适应对象参数的变化并表现出良好的控制品质,具有较强的鲁棒性和自适应能力。
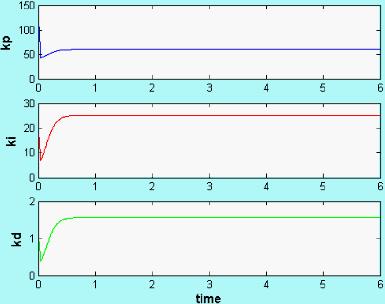
图4 模型时变时,对应kp、ki、kd的变化3.2 基于xPC的液面控制
基于MATLAB软件的xPC半实物仿真平台下,本文利用Simulink将BP神经网络的灰色预测PID算法下载到xPC的目标机,通过xPC双机通信模式进行实时控制,实时控制的结果进一步验证了本文所采用的算法有较好的控制效果,超调量较小,控制精度较高等特点。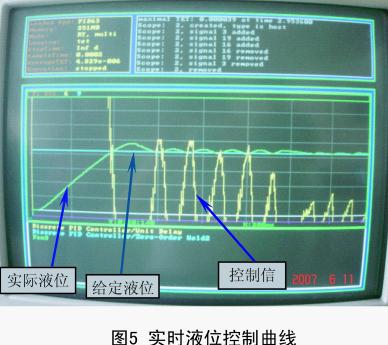
4 结论
本文提出的基于BP网络的智能灰色预测PID控制器,可以同时进行灰色系统的预测和控制。由于BP神经网络具有快速学习的能力,能对系统的未知部分作在线预估控制精度。通过MATLAB离线仿真和xPC技术进行了实时控制结果表明,本文方法可显著提高系统的动态特性,控制效果优于常规的PID控制,能适应时变模型并表现出良好的控制品质,具有较强的鲁棒性和自适应能力。其它作者:
毕效辉(1954-),男,教授,硕士,研究方向为对控制过程进行仿真。
江绍明 西南科技大学 信息工程学院,四川 绵阳 621002
参考文献
[1] 刘思峰,郭天榜,党耀国,等.灰色系统理论及其应用 [M].北京:科学出版社,2000.
[2] 刘金琨. 先进PID控制及其MATLAB仿真 [M].北京:电子工业出版社,2003.
[3] 张利萍,李宏光. 灰色神经网络预测算法在DMF回收过程中的应用[J]. 应用与实践,2007,16(8):1839~1841.
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



