- 基于LMI的广义时滞系统的鲁棒H∞控制
-
企业: 控制网 日期: 2008-05-13 领域: 人机界面 点击数: 1309  廖勇(1982-)
廖勇(1982-)
男,江西崇仁人,硕士研究生,(厦门大学自动化系,福建 厦门 361005),主要研究方向为广义时滞系统的鲁棒控制等。
摘要: 针对一类广义时滞系统,假定系统的状态是完全可测的,基于线性矩阵不等式(LMI),通过构造Lyapunov泛函,给出了一种鲁棒H∞状态反馈控制器的设计,仅通过求解相应的线性矩阵不等式就可得到鲁棒H∞状态反馈控制器。并证明了该方法不仅使得相应的闭环系统渐近稳定,又能保证闭环系统从扰动到受控输出之间传递函数的H∞范数不大于给定的指标值。用数值算例验证了所给方法的有效性。
关键词:广义时滞系统;状态反馈;线性矩阵不等式Abstract: Based on LMI and by proper Lyapunov functions, under the assumption that the system state test is available, H∞ state feedback controllers design can be obtained by solving the corresponding LMI in terms of a generalized time-delay system. This approach is proved that it can not only make the closed-loop systems asymptotically stable, but also limit the H∞ norm of the transfer function from disturbance to controlled output not greater than a given constant. At last, a numerical example is presented to illustrate the validity of this approach.
Key words: generalized time-delay systems; state feedback; LMI
1 引言
众所周知,由于实际系统中元器件的老化,灵敏度不够以及信息传递的延迟,时滞现象广泛存在于各种实际系统中。而时滞的存在常常是许多实际系统不稳定的根源,对正常时滞系统的研究已经取得不少成果[1,2],其控制器设计方法主要集中于用Riccati型的矩阵方程式或不等式方法[3]和线性矩阵不等式(LMI)方法[4]。因为广义时滞系统是比正常时滞系统更加广泛的一类系统,因此对于广义时滞的研究已引起了越来越多的关注。本文研究了一类广义时滞系统H∞控制器的设计,给出了广义时滞系统H∞控制器设计的LMI方法,并可以利用LMI工具箱方便的设计出稳定的控制器。
2 问题的描述
考虑如下形式的广义时滞系统
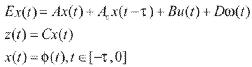 (1)
(1)
其中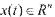 是系统的状态向量,
是系统的状态向量,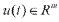 是系统的控制输入向量,
是系统的控制输入向量, 为干扰输入向量,
为干扰输入向量,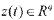 为被控输出向量,
为被控输出向量,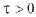 为滞后时间,
为滞后时间,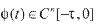 (n维连续函数向量空间)为系统的初始条件。
(n维连续函数向量空间)为系统的初始条件。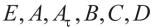 分别是已知的具有适当维数的矩阵,且
分别是已知的具有适当维数的矩阵,且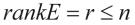 。
。
定义1:对于广义时滞系统(1)的矩阵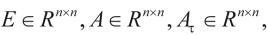 若存在
若存在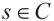 ,使得
,使得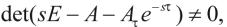 则称系统(1)是正则的。
则称系统(1)是正则的。
定义2:在系统的零初始条件下,对于任意的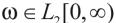 ,给定常数r>0如果有
,给定常数r>0如果有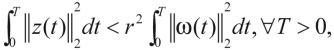 则称系统(1)是渐近稳定的,且具有H∞性能。
则称系统(1)是渐近稳定的,且具有H∞性能。
说明:本文在以下的研究中,我们假定系统(1)是正则的且假定系统无脉冲,正则性保证了系统存在唯一解,而无脉冲保证了系统没有无穷极点。
本文的研究目的是,对于广义时滞系统(1),设计状态反馈控制律
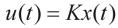 (2)
(2)
使得闭环系统
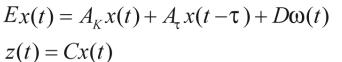 (3)
(3)
是渐近稳定的,且满足一定的H∞性能指标。(其中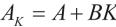 )
)
3 主要结果及证明
以下是本文的第一个结果,给出了闭环系统渐近稳定且具有H∞性能r的充分条件。
定理1对于系统(1)和给定的常数r,如果存在正定对称矩阵Q,矩阵P,使得
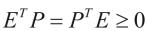 (4)
(4)
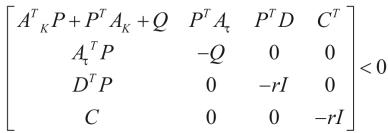 (5)
(5)
则系统(1)具有H∞性能指标r。
证明:构造如下的Lyapunov函数
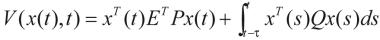 (6)
(6)
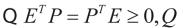 是正定对称矩阵,显然,
是正定对称矩阵,显然, 是正定的。
是正定的。
对(6)式求导得
考虑泛函指标
而
在系统的零初始条件下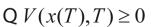 ,所以有
,所以有
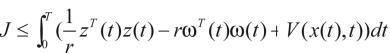

若令
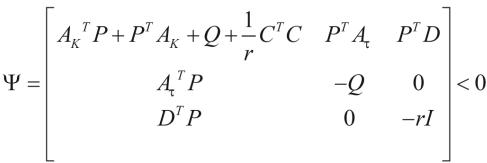 (7)
(7)
则有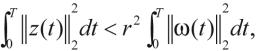 由Schur性质可知,(7)式可以写成如下形式
由Schur性质可知,(7)式可以写成如下形式
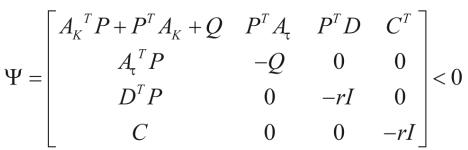 (8)
(8)
定理2给定H∞性能指标r>0,如果存在正定对称矩阵M,非奇异矩阵X和矩阵Y满足
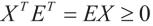 (9)
(9)
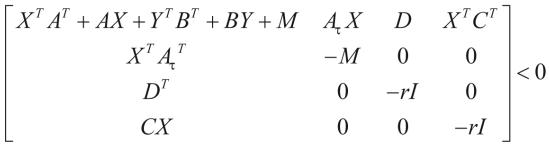 (10)
(10)
则系统(3)是可以状态反馈H∞控制的,且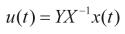 是系统的一个反馈控制律。
是系统的一个反馈控制律。
证明:将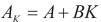 代入(5),并对(4)左乘
代入(5),并对(4)左乘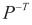 ,右乘
,右乘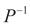 。对(5)左乘
。对(5)左乘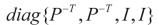 ,右乘
,右乘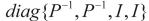 。得
。得
令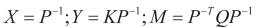 定理可证。
定理可证。
4 算例
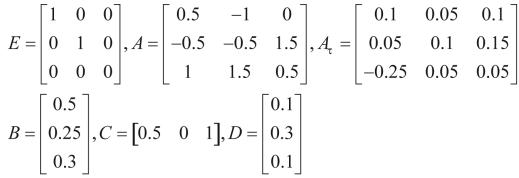
性能指标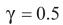 。
。
利用Matlab LMI Toolbox求得:

控制律为
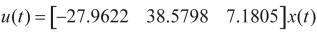
5 结束语
本文研究了一类广义时滞系统的状态反馈H∞控制问题,通过构造Lyapunov泛函给出了稳定控制器设计的线性矩阵不等式(LMI)方法,可以使得闭环系统渐近稳定,且满足一定的H∞性能指标。利用MATLAB软件,可以很方便地设计系统的控制器。因此,本文的结果具有一定的理论和实用价值。其它作者:陈高(1984-),男,江西萍乡人,硕士研究生,主要研究方向为降阶控制器。
参考文献:
[1]Yu L,Chu J.A LMI approach to guaranteed cost control of linear uncertain time-delay systems[J].Automatica,1999,35:1155-1159.
[2]Li X,Souza C E.Criteria for robust stability and stabilization of uncertain linear systems with state delay[J].Automatica,1997,33:1657-1662.
[3]Ball J,Helton J W,Walker M L.Control of nonlinear systems with output feedback[J].IEEE Trans. Automatica,1993,38(4):546-559.
[4]Isidori A,Astolfi A.Disturbance attenuation and H∞ control via measurement feedback in nonlinear systems[J].IEEE Trans.Automatica.Control,1992,37(9):1283-1293.
[5]俞立.鲁棒控制-线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.199-206.
[6]Masubuchi I,Kamitane Y,Ohara A,et al. H∞ control for descriptor systems:a matrix inequalities approach[J].Automatica,1997,33(4):669-673.
[7] Alberto Isidori , Wei Kang. H∞ control via measurement feedback for general nonlinear systems[J]. IEEE Trans. Automat . Contr., 1998, 40 (3):466-472.
[8] Fromion V ,Monaco S ,Normand-cyrot D. The weighted incremental norm approach :from linear to nonlinear H∞ control [J]. Automatica ,2001,37 (10):1585-1592.
[9]陆国平,施也冲,翟其亮.一类不确定时滞系统的鲁棒H∞ 控制[J].系统工程与电子技术, 2002(5):41-44.
[10]付兴建,童朝南.基于LMI的广义不确定时滞系统鲁棒H∞ 控制[J]系统工程与电子技术,2004(12):1876-1878.
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



