- 基于LMI的不确定切换系统极点配置
-
企业: 控制网 日期: 2008-05-13 领域: 工业安全 点击数: 1770  杨延烁(1979-)
杨延烁(1979-)
男,福建福州人,硕士研究生,(厦门大学自动化系,福建 厦门 361005),主要研究方向为切换系统的极点配置和鲁棒性。
基金项目:福建省青年科技人才创新项目基金(2005J006),厦门大学985二期信息创新平台项目。
摘要:研究了一类不确定线性切换系统基于状态反馈的极点配置和LMI方法问题。此类切换系统不仅具有未知但有界的结构不确定性,而且具有外部扰动。利用公共Lyapunov函数,得到一稳定切换控制策略来保证:(1)各线性子系统的特征值位于左半复平面的选定圆内,(2)最小化闭环切换系统的扰动衰减水平。在各子系统不稳定的前提下,设计切换系统的状态反馈控制器,使得在任意切换策略下系统的闭环极点配置在左半复平面,且具有良好的扰动衰减水平,系统渐近稳定。得到了切换系统可状态反馈镇定的充分条件;然后用易于求解的线性矩阵不等式形式表示出结果;最后通过仿真验证所设计的切换系统在状态反馈控制器下渐近稳定,且具有良好的极点配置和最小衰减水平。
关键词:切换系统;极点配置;状态反馈;LMI方法;衰减水平Abstract: The problem of state feedback control of continuous-time switched linear systems with uncertain items is addressed in this paper. Uncertain switched systems’ pole assignment and disturbance attenuation level are studied. The switched systems not only have unknown, norm-bounded uncertainty in system’s structure, but also have exogenous disturbance. By using common Lyapunov function method, the state feedback robust controllers under arbitrary switching strategy are designed to assure each subsystem’s eigenvalue inside a chosen circle on the open left-half complex plane and the states of the systems asymptotically stable. Then the minimum disturbance attenuation level on Lyapunov function for switched systems is obtained. Both of the pole assignment and minimum disturbance attenuation level of switched systems are obtained. All of these based on convex combinations technique and linear matrix inequalities method, the result is expressed in the form of linear matrix inequalities, which can be solved easily. Finally the simulation shows that the designed controller can make the states of the switched systems asymptotically stable under the arbitrary switching strategy with poles inside chosen circles and minimum disturbance attenuation level.
Key words: switched systems; pole assignment; state feedback; LMI approach; attenuation level
1 引言
目前切换系统应用在航空、通讯、机械生产等多方面,并引起了多方面的重视[1-3]。切换系统与单一系统比较,其系统的稳定性与各子系统的稳定性密切相关,又由于存在切换策略的影响,子系统稳定并不一定使得总系统稳定。值得一提的是切换控制策略对于提高系统的性能起了重要作用,保证了系统的鲁棒性和实现了控制方案。近几年研究的问题主要有:(1)找到在任意切换下实现系统稳定的条件,(2)找到实现系统稳定的切换策略,(3)找到实现系统某些性能指标的条件。
利用固定增益得到的二次镇定的主要缺点是结果可能过于保守,也就是,通过切换策略切换系统能够实现镇定,但是不能保证存在一个对于所有子系统都成立的常值反馈镇定阵。近来取得了不少基于二次Lyapunov函数的切换控制策略的研究成果,如文献[4]通过一个状态依赖切换策略来镇定切换系统,文献[5]用状态和输出反馈以及LMI方法来研究连续时间切换线性系统的二次镇定问题。
切换系统稳定性和鲁棒镇定的研究取得了不少成果[6-9]。文献[6]进行了混杂切换系统的稳定性分析和镇定问题的研究。文献[7]考虑了一类离散线性切换系统的二次稳定化状态反馈控制律的设计问题,利用多李亚普诺夫函数法推导了在任意切换下二次稳定控制律存在的充分条件,同时提供了二次稳定控制律的一个参数化表示。文献[8]利用Lyapunov函数方法研究了一类带有外部扰动的切换系统。解决了极点配置和扰动衰减水平的问题。但是没有考虑带有不确定项的切换系统的相应问题。
本文研究了一类具有不确定项和扰动的切换系统,不确定项是未知有界的,考虑了通过设计状态反馈控制器实现闭环系统的极点配置在左半复平面给定圆心和半径的圆域内,同时满足系统的稳定要求,以及闭环系统的H∞衰减水平的上界。极点配置提高了系统的动态响应,H∞衰减水平的最小化确保在受到能量信号扰动下切换系统的鲁棒性。假定切换规则和状态向量是未知但实时可测的。基于公共二次李亚普诺夫函数,用LMI方法确定状态反馈增益,来镇定闭环系统,同时满足极点配置和H∞性能要求。最后给出了数例,验证了所设计方法的可行性和有效性。2 问题描述
考虑下面具有不确定性的线性切换系统
(1)
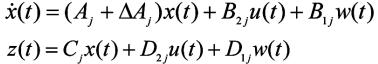
(2)
其中。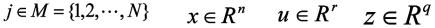 分别是系统的状态、控制输入和输出向量。
分别是系统的状态、控制输入和输出向量。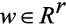 是外部扰动。
是外部扰动。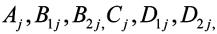 分别是第j个子系统的系统矩阵,△Aj是结构不确定项。
分别是第j个子系统的系统矩阵,△Aj是结构不确定项。
假设1:不确定项可分解如下形式
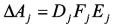 且
且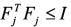 (3)
(3)
其中Dj与Ej为适当维数的常数矩阵, Fj是适当维数的未知矩阵。
引理1:对任意具有适当维数的矩阵X,Y及实数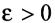 ,都有
,都有
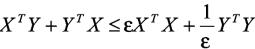 (4)
(4)
3 主要结果
先考虑无外部扰动的系统(1)和(2),也就是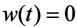 ,要找到一个状态控制器,使得闭环系统
,要找到一个状态控制器,使得闭环系统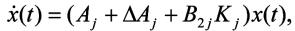 渐近稳定。下面的定理1给出了一个充分条件。
渐近稳定。下面的定理1给出了一个充分条件。定理1. 如果存在一个正定矩阵
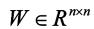 和矩阵
和矩阵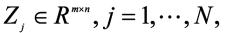 及实数
及实数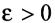 ,使得
,使得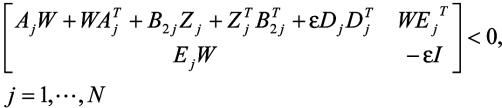 成立。
成立。
状态反馈控制器为
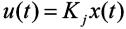 , (6)
, (6)
其中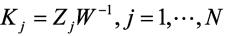
则闭环系统在任意切换策略下稳定。
证明:由(5)得
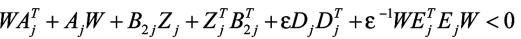
闭环系统稳定可由存在公共Lyapunov函数实现,即
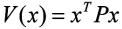 令
令 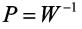
则
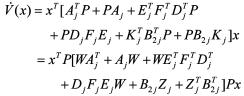
由引理1得
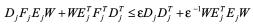
则
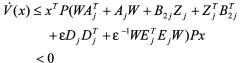
证毕。定理1给出了使闭环系统
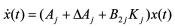 渐近稳定的充分条件,但要使闭环系统的极点配置在以
渐近稳定的充分条件,但要使闭环系统的极点配置在以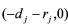 为圆心,rj为半径的圆内,表示为
为圆心,rj为半径的圆内,表示为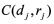 ,即
,即
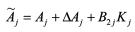 (7)
(7)
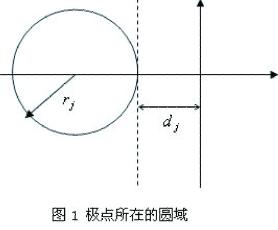
的极点配置在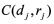 内,如图1所示。那么下面的定理2给出了充分条件。
内,如图1所示。那么下面的定理2给出了充分条件。
在以下的证明中为了简洁,设
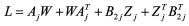 (8)
(8)
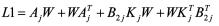 (9)
(9)
定理2 如果存在对称正定阵
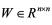 和矩阵
和矩阵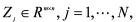 及实数
及实数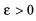 ,使得
,使得
 (10)
(10)则闭环系统的极点可配置在
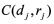 内,且系统稳定。
内,且系统稳定。
证明:由(10) 可得
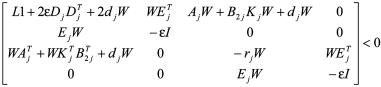
定义矩阵
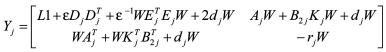
那么
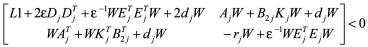
等价于

由引理1得
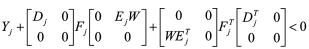
展开得

即
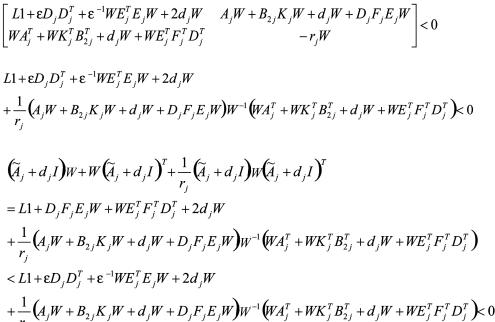
该式满足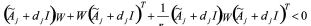
从而由文献[9]的结果知,上述条件实现了极点配置。
且
 (11)
(11)
该式保证系统稳定。 证毕。
从定理2可得到以下结论:如果圆心和半径选择适当,子系统将以理想的速度渐近衰减。通过适当地选择 ,每个子系统的闭环响应能独立设计。
,每个子系统的闭环响应能独立设计。 能用来限制每一子系统的瞬态响应范围。例如,基于数值
能用来限制每一子系统的瞬态响应范围。例如,基于数值 ,系统瞬态响应的调整时间为
,系统瞬态响应的调整时间为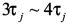 。
。 可以确定瞬态响应振动频率的上界。
可以确定瞬态响应振动频率的上界。
接下来考虑带有扰动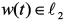 的系统(1)-(2),以下定理3将给出最小化系统衰减水平的方法,通过给每个子系统一个增益阵,保证闭环系统在任意切换下稳定且得到系统最小
的系统(1)-(2),以下定理3将给出最小化系统衰减水平的方法,通过给每个子系统一个增益阵,保证闭环系统在任意切换下稳定且得到系统最小 衰减水平。
衰减水平。
定理3 如果存在一个公共正定矩阵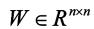 和矩阵
和矩阵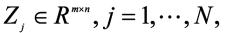 及实数
及实数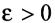 ,使得
,使得
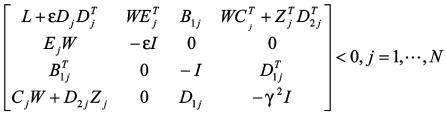 (12)
(12)
则闭环系统满足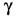 衰减水平,即对于任一输入
衰减水平,即对于任一输入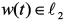 确定一个边界
确定一个边界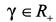 ,使得
,使得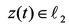 满足
满足 。
。
证明:由(11)可得
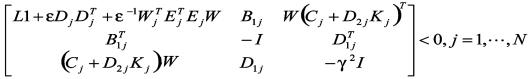
由上式可得
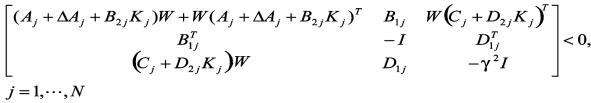 (13)
(13)
该式保证了系统的H∞最小衰减水平。
证毕。
通过定义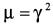 ,且在满足(12)式的前提下最小化
,且在满足(12)式的前提下最小化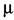 ,可以求得最小的H∞保成本。(12)式的可行解给每个子系统一个增益Kj和公共Lyapunov矩阵W,确保切换系统在任意切换下实现H∞保成本。实际上,对每个子系统可以设定一个
,可以求得最小的H∞保成本。(12)式的可行解给每个子系统一个增益Kj和公共Lyapunov矩阵W,确保切换系统在任意切换下实现H∞保成本。实际上,对每个子系统可以设定一个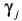 ,公共Lyapunov矩阵确保系统全局稳定,而
,公共Lyapunov矩阵确保系统全局稳定,而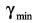 则是最差情况下H∞保成本。
则是最差情况下H∞保成本。
通过定理1-3,我们既能确定切换控制律来实现每一子系统的极点配置,也能确定一个扰动衰减水平来提高切换系统的鲁棒性。以下的定理4则给出了同时满足状态反馈下实现闭环极点配置和最小化衰减水平的充分条件。
定理4如果存在一个公共正定矩阵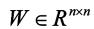 和矩阵
和矩阵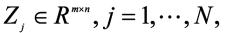 及实数
及实数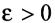 ,使得
,使得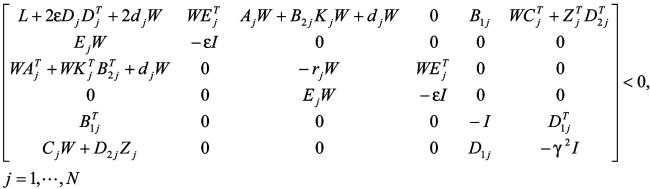
成立,则带状态反馈的闭环系统既满足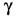 衰减水平,极点配置在
衰减水平,极点配置在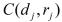 内,且闭环系统稳定。
内,且闭环系统稳定。
证明:
由Schur定理及(14)式可得
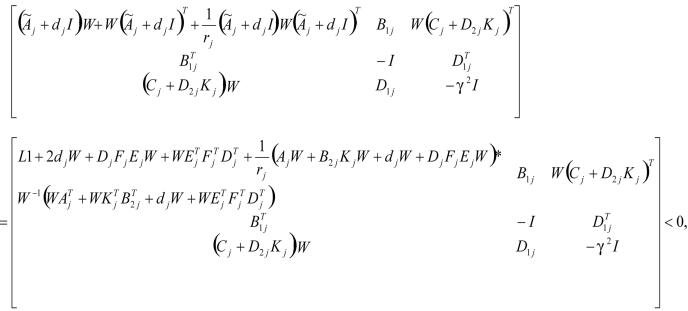
该式保证了(11)式和(13)式成立,就实现了极点配置和最小化衰减水平。
4 例子
例1考虑以下切换系统,有两个子系统,矩阵分别为
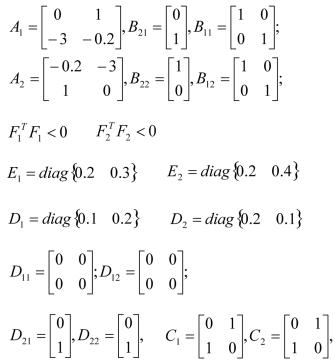
该切换系统在初始状态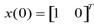 和切换规则每0.5秒切换一次下是不稳定的,如下图2所示。
和切换规则每0.5秒切换一次下是不稳定的,如下图2所示。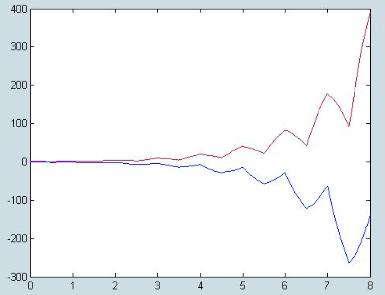
图2 切换系统状态变量轨迹通过使用定理1-4于该切换系统,能得到渐近稳定的结果。如用定理2,可得到各子系统极点配置在
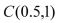 内且全局稳定的结果。
内且全局稳定的结果。
图3给出了在初始条件和切换规则下经过状态反馈和极点配置的状态响应曲线。实线代表使用定理2后闭环系统的状态变量的轨迹,虚线是只确保状态稳定的状态轨迹。比较可看出,有极点配置的曲线更光滑且更快的瞬时响应。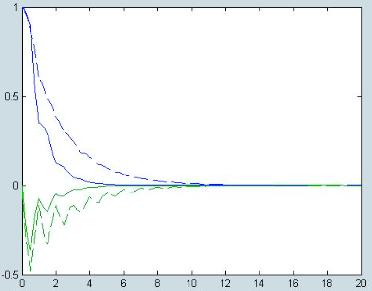
图3 闭环切换系统状态变量的轨迹应用定理3可得出一个控制器来提高扰动衰减水平,应用定理4既得到良好的极点配置,又使系统具有最小的
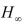 衰减水平,且系统渐近稳定,如图4所示。
衰减水平,且系统渐近稳定,如图4所示。
应用定理4得到的增益矩阵为

Lyapunov 矩阵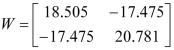
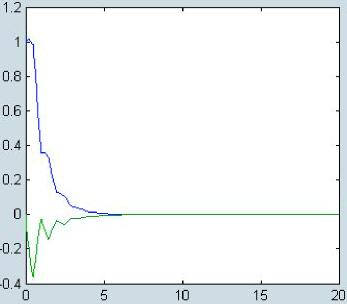
图4 状态反馈响应曲线4 结论
文章中的状态反馈控制律保证了切换闭环系统的每个子系统的极点配置在左开半复平面的指定圆内,也保证了闭环切换系统在给定 衰减水平下的全局稳定。数例说明切换控制策略可解决更严格的设计要求,基于公共二次李亚普诺夫函数的方法提高了该类系统的动态响应。LMI公式化条件可进一步用于解决离散或输出反馈问题。
衰减水平下的全局稳定。数例说明切换控制策略可解决更严格的设计要求,基于公共二次李亚普诺夫函数的方法提高了该类系统的动态响应。LMI公式化条件可进一步用于解决离散或输出反馈问题。其它作者:
张霄力(1970-),男,河北唐县人,副教授,博士,主要研究方向为混合系统、切换系统的稳定性等。参考文献:
[1] Guisheng Zhai,Derong Liu,Joe Imae, Tom-oaki Kobayashi.Lie Algebraic Stability Analysis for Switched Systems With Con- tinuous-Time and Discrete-Time Subsyst- ems[J]. IEEE transactions on circuits and systems- II: EXPRESS BRIEFS, 2006, 53(2):152-156.
[2] Zhendong Sun. Stabilization and optimi- zation of switched linear systems [J]. Automatica 2006, 42:783–788.
[3] Changzhi Wu, Kok Lay Teo, Rui Li,Yi Zh- ao.Optimal control of switched systems with time delay [J].Applied Mathematics Letters 2006,19:1062-1067.
[4] G.S. Zhai, H. Lin, P.J. Antsaklis, Quadratic stabilizability of switched linear systems with polytopic uncertainties, Internat. J. Control 76 (7) (2003) 747–753.
[5] Z. Ji, L.Wang, G. Xie, F. Hao, Linear matrix inequality approach to quadratic stabilization of switched systems, IEE Proc. Control Theory Appl. 151 (3) (2004) 289–294.
[6] Xuping Xu, Guisheng Zhai. Practical stability and stabilization of hybrid and switched systems [J]. IEEE transa- ction on automatic control,2005, 50(12): 1897-1903.
[7] 陈松林,姚郁。一类离散时间线性切换系统的二次鲁棒镇定[J].信息与控制2005, 34(4):393-397.
[8] V.F.Montagner, V.J.S.Leite,R.C.L.F. Oliveira, P.L.D. Peres.. State feedback control of switched linear systems: An LMI approach [J]. Computational and Applied Mathematics, 2006, 194: 192-206.
[9] W.M. Haddad, D.S. Bernstein, Controller design with regional pole constrains, IEEE Trans. Automat. Control 37(1) (1992)54-69.
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



