- 带有丢包的NBFI控制系统满足H∞性能指标的研究
-
企业: 控制网 日期: 2008-06-15 领域: PLC&PAC 点击数: 1666  李理(1980-)
李理(1980-)
男,(厦门大学自动化系,福建 厦门 361005),厦门大学自动化系硕士研究生,研究方向为网络控制系统。
摘要:基于网络的反馈连接系统(NBFIs)是一种新型的基于网络连接的系统模型。本文主要研究带有扰动输入的网络丢包问题,即系统在满足一定数据丢包率和一定H 性能指标的条件下具有的状态反馈控制问题。首先把网络看作一个开关,将带有丢包的NBFI系统建模为带有结构事件率约束的异步动态系统(ADSs);其次运用平均驻留时间方法与H 控制理论,推导出由ADS系统进一步建模成的切换系统指数稳定同时满足一定H 性能指标的充分条件;最后以数值例子仿真验证结论的有效性。
关键词:网络控制系统;基于网络的反馈连接;平均驻留时间;异步动态系统;H 性能Abstract: NBFI is a new kind of network-based model. For the network-induced packet dropout, an average dwell time method is used to analyze the Network-based H Control of NBFIs. First of all, the NBFI with data packet dropout is modeled as an asynchronous dynamical system with rate constraints on events. Then, by using the average dwell time method and applying H control theories, a sufficient condition of the NBFI stability with H performance bound is obtained. Finally, a simulation example is given to illustrate the effectiveness of the proposed approach.
Key words: networked control system;network-based feedback interconnection;average dwell time;asynchronous dynamical system;H performance
1 引言
随着网络在社会各个领域的广泛应用,许多专家学者也开始关注和研究基于网络连接的系统,而通过实时网络连接形成的闭环反馈控制系统称为网络控制系统(如图1)(networked control systems,NCSs)[1][2]。它的主要特点是系统的各个器件(传感器、控制器、执行器等)是通过实时网络来进行数据信息交换的。网络控制系统相对于传统的点对点控制类系统,具有轻便,易操作、维修,有较高的灵活性、可靠性等优点。因此网络控制系统在航空航天,制造业等领域有广泛的应用。然而,因为网络的存在也为控制系统带来相应的问题:信息的传输延迟[1][3] ;受网络带宽和数据包容量的限制,须采用多通道传输等[1][4] ;由于网络传输的不可靠性,网络控制系统发生数据包丢失现象。
在网络控制系统中,当节点出现故障或发生信息传送碰撞时,就可能出现丢失网络数据包的现象。虽然大多数网络具有重新传输机制,但它们也只能在一个有限的时间内传输,当超过这个时间后,数据也会随之丢失。文[1][5][6][7]把数据包丢失的NCS系统建模为具有事件率约束的异步动态系统(ADSs),并研究了此异步动态系统的稳定性问题。文[8][9][10]介绍了最大允许传输间隔(MATI)这个概念,它是指如果网络发生丢包,则两次成功传输的时间间隔不大于MATI。文[11][12][13][14][15]把带有丢包的NCS系统建模为一个切换系统,在此基础上分析了系统的稳定性。如,文[14]针对网络丢包现象,设计出新的控制器并运用切换系统的平均驻留时间方法研究系统的稳定性;文[15]针对网络丢包现象提出一个特殊的不确定切换系统模型,并研究了该模型的鲁棒反馈控制问题。有时,所研究的NCS 系统带有不确定参数[12][15][17]。如,文[17]针对不确定NCS系统,设计出鲁棒反馈控制器H 解决网络丢包问题。有时,网络延迟和网络丢包是被同时考虑的[7][11][12][16][17]。如,文[7][16]利用Lyapunov方法推导出带有延迟和丢包现象的NCS系统稳定的充分条件。
文[19]提出了一种新型的反馈连接系统(如图2),它是将传统的反馈连接通过网络来实现,因此也可将其看作是基于网络的反馈连接(Network-Based Feedback Interconnection,NBFI)。同时它也可看作是NCS系统的扩展模式,NCS系统是通过网络使被控对象和控制器相连接,形成一个闭环反馈系统。而NBFI系统是两个被控对象通过网络连接形成的闭环反馈系统。因为网络的存在,NBFI系统也会出现延迟或丢包等现象。文[19]利用耗散性理论研究了NBFI系统的丢包问题,但是它仅仅针对每个被控对象都是离散系统的情况,而每个被控对象为连续系统的情形没有考虑。
受文[19]的启发,本文研究了由连续对象通过网络串联而成的NBFI系统。应用网络发生丢包时数据传输为零这一特性,把系统建模为一个带有事件率约束的异步动态系统。分析开关断开或闭合时系统运行的各个状态,把这个异步动态系统进一步建模为带有四个子系统的切换系统。以此为基础,研究了该种类模型满足H 性能指标的反馈控制问题,通过引入一个新的切换策略,即运用切换系统的平均驻留时间方法,使得系统在满足小于一定的丢包率的条件下,对于每一个具有平均驻留时间的系统状态都能够保证系统全局渐近稳定,同时又可使系统满足一定的H 性能指标的要求。
在文章的第二部分将会描述NBFI系统,并给出网络正常传输和非正常传输时系统的数学模型。第三部分将分析系统的稳定性同时使系统满足一定H 性能指标的要求。第四部分给出一个数值算例验证本文方法的有效性。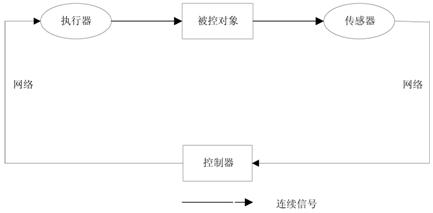
图1 典型网络控制系统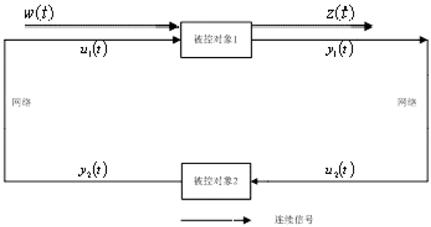
图2 基于网络的反馈连接系统
图3 带有丢包的NBFI系统2 系统分析与建模
把图2所示的带有扰动输入的NBFI系统。
假设系统满足如下条件:
假设1 网络传输正常情况下,系统近似看作为带有扰动的无时滞连续线性系统。
假设2 网络采用单包传输模式,左右网络发生数据包发丢失情况不确定。
假设3 丢包总的发生时刻在整个系统时间定义域内小于或等于一定比率。
假设4 系统中仅有一个被控对象受外界扰动信号干扰。
则系统可建模为一个连续的常规反馈连接系统:
 (1)
(1)
其中状态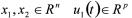 为被控对象1的输入,
为被控对象1的输入,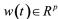 为被控对象1的扰动输入,
为被控对象1的扰动输入,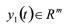 为被控对象1的输出,
为被控对象1的输出,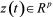 为被控对象1的受控输出,
为被控对象1的受控输出,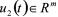 为被控对象2的输入,
为被控对象2的输入,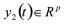 为被控对象2的输出,A1,A2′,B1,B2,B1′,C1,C2,D是具有适当维数的常数矩阵。
为被控对象2的输出,A1,A2′,B1,B2,B1′,C1,C2,D是具有适当维数的常数矩阵。
当网络发生数据包丢失时,网络可以视为按一定速率开合的开关[1][5][6]。带有数据包丢失的NBFI系统描述如图3所示 :右网络视为开关S1,左网络视为开关S2,当左右开关同时闭合时(S1 S2),网络正常传输即系统不发生丢包现象;当左右开关同时打开(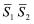 )或只有一个开关打开而另一个开关闭合(S1,S2)时,网络非正常传输即系统发生丢包现象。下面列写系统在这四种情况下运行的状态方程:
)或只有一个开关打开而另一个开关闭合(S1,S2)时,网络非正常传输即系统发生丢包现象。下面列写系统在这四种情况下运行的状态方程:
情况一 (S1 S2):
(S1 S2):
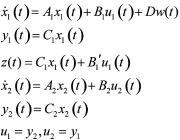
令 ,则
,则
 。 (2)
。 (2)
情况二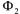 (
(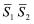 ):
):
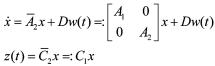 。 (3)
。 (3)
情况三 (
(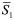 S2):
S2):
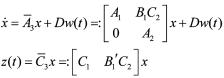 。 (4)
。 (4)
情况四 (S1
(S1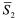 ):
):
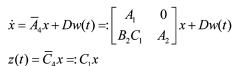 。 (5)
。 (5)
可以把系统在这四种情况下的运行视作系统在四个子系统间的切换,则
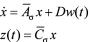 , (6)
, (6)
其中状态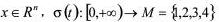 为切换信号,它是一个依赖于时间t或状态x的分段右连续常值函数,
为切换信号,它是一个依赖于时间t或状态x的分段右连续常值函数,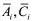 是具有适当维数的常数矩阵。
是具有适当维数的常数矩阵。
定义1[7] 对应于异步动态系统四种状态 事件出现的比率,称为结构事件率。
事件出现的比率,称为结构事件率。
用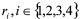 分别表示每一状态的结构事件率,
分别表示每一状态的结构事件率,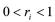 。显然r满足
。显然r满足
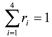 。
。
因此当网络中数据包丢失率一定时,由异步动态系统进一步建模成的切换系统同样受到结构事件率ri的约束。
3 主要结果
对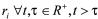 ,引入符号
,引入符号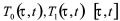 ,分别表示在时间内网络正常传输与非正常传输(网络丢包)的时间长度。
,分别表示在时间内网络正常传输与非正常传输(网络丢包)的时间长度。
定义2 [15] 对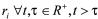 , 如果存在0<P<1,
, 如果存在0<P<1,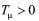 使得下面不等式
使得下面不等式
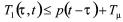 , (7)
, (7)
成立,则称p为系统在时间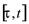 上的最大丢包率。
上的最大丢包率。
因为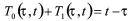 ,所以从上面的定义中,我们可以得到
,所以从上面的定义中,我们可以得到
 , (8)
, (8)
这里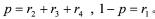 。
。
定义3 [18] 对切换信号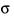 ,用
,用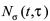 表示在时间段
表示在时间段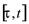 上切换的次数。如果存在数
上切换的次数。如果存在数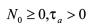 使得对任何的
使得对任何的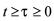 都有
都有
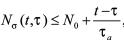 (9)
(9)
成立,那么称正数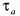 为平均驻留时间。
为平均驻留时间。
注1:平均驻留时间的提出是为了限定切换系统中任意两次切换的时间间隔,因此满足平均驻留时间就是指系统在一段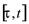 时间内的任意两次切换的时间间隔不小于一个时间值
时间内的任意两次切换的时间间隔不小于一个时间值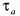 ,以避免因切换过快而导致的系统不稳定。
,以避免因切换过快而导致的系统不稳定。
定理1 若存在正定对称矩阵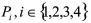 和正数
和正数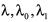 ,使得下列矩阵不等式
,使得下列矩阵不等式
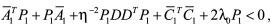 , (10)
, (10)
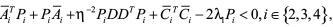 , (11)
, (11)
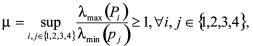 (12)
(12)
成立。如果最大丢包率满足
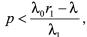 (13)
(13)
并且在满足平均驻留时间
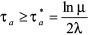 (14)
(14)
的切换律下,系统是指数稳定的,且是具有H∞性能指标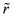 。这里
。这里
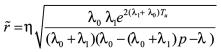
证明:
1) 当外部扰动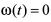 时,系统(6)的渐近稳定性。
时,系统(6)的渐近稳定性。
定义分段Lyapunov函数
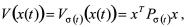 (15)
(15)
其中Pi为满足式(10)、式(11)、和式(12)的正定对称矩阵。
则由式(12)得
 。 (16)
。 (16)
对于式(15),存在两个正数a和使得b
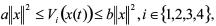 (17)
(17)
其中 。
。
当切换到第i个子系统时,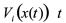 沿着相应的子系统对时间t的导数为
沿着相应的子系统对时间t的导数为
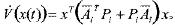 (18)
(18)
由式(10)、(11)、(18),得
 (19)
(19)
 (20)
(20)
定义为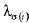 系统对切换信号
系统对切换信号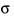 在t时刻状态下满足式(19)、式(20)的
在t时刻状态下满足式(19)、式(20)的 或
或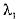 值。则对
值。则对 ,令
,令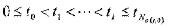 表示系统在时间段(0,t)上的切换点,由式(16)、式(17)和式(20)可得
表示系统在时间段(0,t)上的切换点,由式(16)、式(17)和式(20)可得
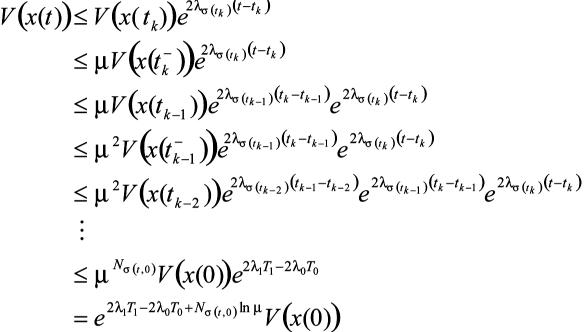 (21)
(21)
如果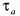 满足条件(14),即对
满足条件(14),即对 ,
,
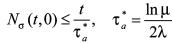
成立,则
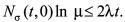 (22)
(22)
把式(7)、(8)、(22)代入式(21),可得
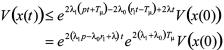 (23)
(23)
由式(13)、(23),根据欧式范数的定义有
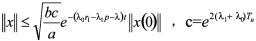
所以系统(6)在满足平均驻留时间(14)的切换律下是指数稳定的,且指数衰减率。
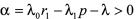
注2:当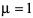 时,Pi=Pj,
时,Pi=Pj,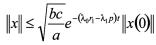 ,则系统在满足
,则系统在满足 条件时,系统在任意切换下是全局渐近稳定。
条件时,系统在任意切换下是全局渐近稳定。
2) 系统满足H∞性能指标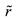 的稳定性。
的稳定性。
网络持续丢包和正常传输是交替进行的,则对 ,令
,令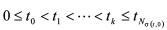 表示系统在时间(0,t)段上的切换点,那么r1事件与事件
表示系统在时间(0,t)段上的切换点,那么r1事件与事件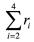 发生的时间区间集合分别为:
发生的时间区间集合分别为:
持续丢包事件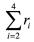 发生的时间区间集合:
发生的时间区间集合: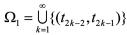 ,
,
正常传输事件r1发生的时间区间集合: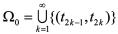 。
。由矩阵不等式(10),(11)可得
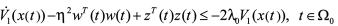 (24)
(24)
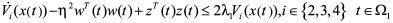 (25)
(25)
由式(15),式(23),式(24),则对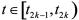 ,有
,有
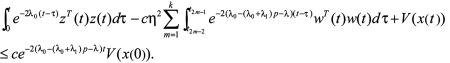 (26)
(26)
由式(15),式(23),式(25),则对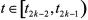 ,有
,有
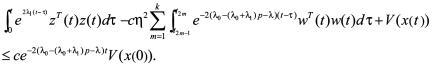 (27)
(27)
由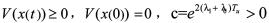 ,则有
,则有
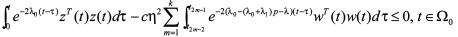 (28)
(28)
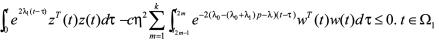 (29)
(29)
把式(28),式(29)合并,可得在
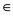 R+有
R+有
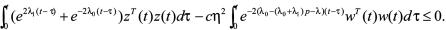 (30)
(30)
将式(30)中t从0→∞进行积分,可得
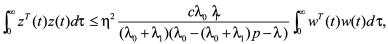 (31)
(31)
即
所以系统具有H∞性能界 ,定理得证。
,定理得证。
4 仿真
对于NBFI系统,设参数矩阵为:
取系统的初始点 。如图4、5、6,NBFI系统运行在网络发生丢包时是不稳定的:
。如图4、5、6,NBFI系统运行在网络发生丢包时是不稳定的: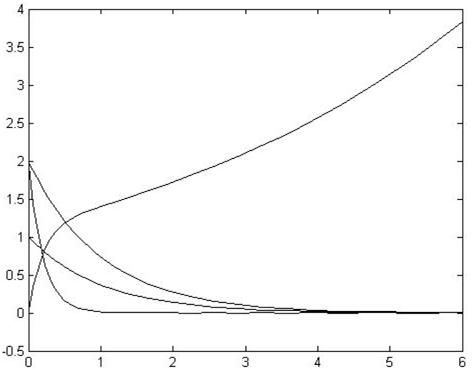
图4 NBFI系统左右网络同时发生丢包现象的状态响应图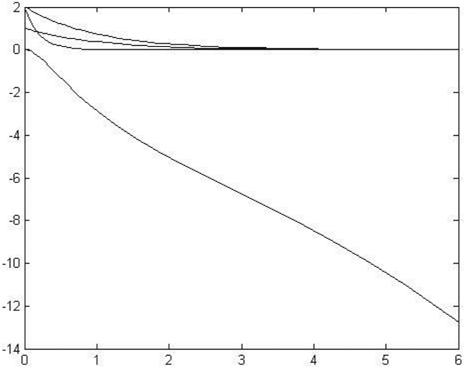
图5 NBFI系统右网络发生丢包现象的状态响应图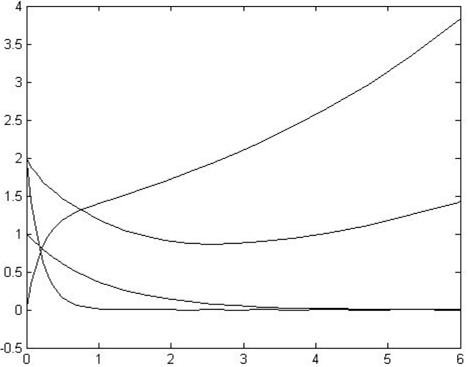
图6 NBFI系统左网络发生丢包现象的状态响应图设
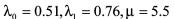 ,应用MATLAB求解LMI式(24)、(25)、(26),得到正定对称矩阵:
,应用MATLAB求解LMI式(24)、(25)、(26),得到正定对称矩阵:
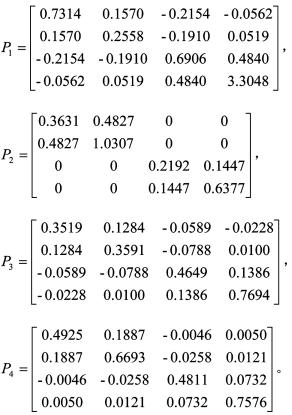
令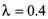 ,由
,由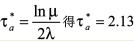 ,对切换系统(5),取驻留时间
,对切换系统(5),取驻留时间 ,则由条件(13)得出系统的最大丢包率
,则由条件(13)得出系统的最大丢包率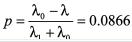 。
。
对切换系统(6)进行随机切换,应用MATLAB中的rand函数随机产生一组由1,2,3,4生成的随机数列,其中1,2,3,4分别代表系统的四个子系统。在满足平均驻留时间和最大丢包率的情况下,应用随机产生的这组数列设计切换律(如图7)。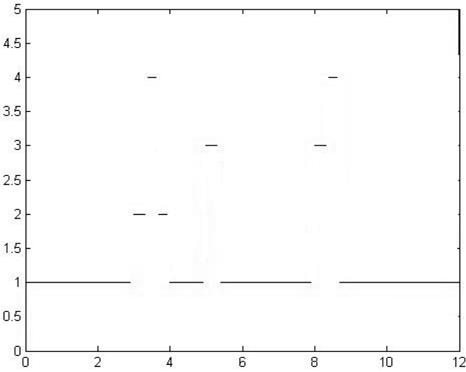
图7 系统(6)的切换律曲线图运行后,则可得切换系统(6)的状态响应图(如图8)。
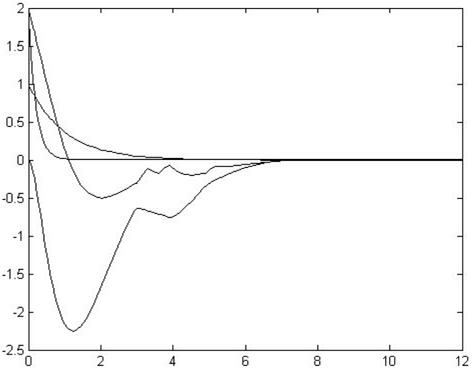
图8 切换系统(6)的状态响应图从图8可看出切换系统(6)在满足一定的驻留时间和丢包率的情况下能够收敛。且此时若
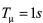 ,相应的H∞性能指标
,相应的H∞性能指标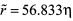 ,若
,若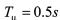 ,相应的H∞性能指标下降到
,相应的H∞性能指标下降到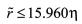 。
。
5 结论
本文研究了基于网络传输的新型反馈连接系统。因为系统的反馈连接是通过网络来实现的,所以系统运行时依然会出现延迟或丢包现象。为此对连续的带有丢包情况的NBFI系统进行异步动态系统建模,得到系统运行的四种状态,由此把带有丢包的NBFI系统视为在四种状态间切换的切换系统,然后运用平均驻留时间方法和H∞控制理论,使得每次切换后在该子系统的驻留时间不小于一个定值时,保证系统在一定的丢包范围内是渐近稳定的,且满足一定H∞性能界要求。本文仅就连续线性系统的丢包问题进行了研究,并没有考虑网络发生延迟或多包传输等情况,而且将来也需要对非线性的NBFI系统所发生的各种问题进行细致的研究。
其他作者:
孙洪飞,男,厦门大学信息科学与技术学院副教授,研究方向为切换系统与网络控制系统。
参考文献:
[1] W. Zhang ; M. S. Branicky ; S. M. Phillips . Stability of Networked Control Systems , Control System Magazine , IEEE Vol. 21 ,Issue 1, Feb. 2001 Page(s):84 - 99.
[2] G. C. Walsh ; Y. Hong ; L. G. Bushnell . Stability Analysis of Networked Control Systems , Control Systems Technology , IEEE Transactions on Vol. 10 ,Issue 3, May 2002 Page(s):438 - 446.
[3] L. Q. Zhang ; S. Yang; T. W. Chen ; B. Huang . A New Method for Stabilization of Networked Control Systems With Random Delays , Automatic Control , IEEE Transactions on Vol. 50 ,?Issue 8, Aug. 2005 Page(s):1177 - 1181.
[4] S. Mastellone ; C. T. Abdallah ; P. Dorato . Model-based Networked Control for Nonlinear Systems with Stochastic Packet Dropout , American Control Conference , vol. 4 , June 2005 Page(s):2365 – 2370.
[5] A. Hassibi ; S. P. Boyd ; J. P. How . Control of Asynchronous Dynamical Systems with Rate Constraints on Events , Decision and Control , 1999. Proceedings of the 38th IEEE Conference on Vol. 2 ,?7-10 Dec. 1999 Page(s):1345 - 1351 .
[6] A. Rabello ; A. Bhaya . Stability of Asynchronous Dynamical Systems with Rate Constraints and Application , American Control Conference , 2002. Proceedings of the 2002 Vol. 2 ,?8-10 May 2002 Page(s):1284 - 1289 .
[7] Z. Z. Qiu ; Q. L. Zhang ; Z. C. Lian ; M. Liu . Exponential Stability of State Feedback Networked Control System with Time-delay and Data Packet Dropout, Information and Control , vol. 34 , Oct. 2005 Page(s):567-575.
[8] G. C. Walsh ; H. Ye ; L. Bushnell . Stability Analysis of Networked Control Systems , Proceedings of American Control Conference , 1999 Page(s).:2876-2880.
[9] G. C. Walsh ; O. Beldiman ; L. Bushnell . Asymptotic Behavior of Networked Control Systems , Proceedings of the International Conference on Control Applications , 1999 Page(s): 1448- 1453.
[10] O. Beldiman ; G. C. Walsh ; L. Bushnell . Predictors For Networked Control Systems , Proceedings of American Control Conference , 2000 Page(s): 2347- 2351.
[11] M. Yu, L. Wang ; T. G. Chu ; G. M. Xie . Stabilization of Networked Control Systems with Data Packet Dropout and Network Delays via Switching System Approach , Proceedings of the 43rd IEEE Conference on Decision and Control , Bahamas , 2004 Page(s): 3539-3544.
[12] H. Lin ; G. S. Zhai ; P. J. Antsaklis ; Robust Stability and Disturbance Attenuation Analysis of A Class of Networked Control Systems , Proceedings of the 42th IEEE Conference on Decision and Control , 2003 Page(s): 1182-1187.
[13] P. V. Zhivoglyadov ; R. H. Middleton . Networked Control Design for Linear Systems , Automatica , vol. 39, no. 4, 2003 Page(s): 743-750.
[14] D. Ma ; J. Zhao . Stabilization of Networked Control Systems via Switching Controllers: an Average Dwell Time Approach , Intelligent Control and Automation , 2006. WCICA 2006. The Sixth World Congress on Volume 1, 2006 Page(s):4619 - 4622.
[15] J. Huang ; Z. H. Guan ; Z. D. Wang . Robust Control with Performance Bound for Networked Control Systems with Data Packet Dropouts , Control and Decision , vol.20, Sep. 2005 Page(s):1002-1005.
[16] J. L. Xiong ; J. Lam . Stabilization of Linear Systems Over Networks with Bounded Packet Loss , Automatica , vol. 43, no. 1 , 2007 Page(s):80-87.
[17] D. Yue ; Q. L. Han ; J. Lam . Network-based Robust? Control of Systems with Uncertainty , Automatica , vol. 41, no. 6 , 2005 Page(s):999-1007.
[18] A. S. Morse . Supervisory Control of Families of Linear Set-point Controllers , Automatic Control , IEEE Transactions on Volume 41, Issue 10,? Oct. 1996 Page(s):1413 - 1431。
[19] H. F. Sun ; D. J. Hill . Stability of Network-based Feedback Interconnection , Submitted to Automatica , 2007
编号:080532
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



