- 模糊化方法的研究
-
企业: 控制网 日期: 2008-08-11 领域: 工业安全 点击数: 3830 
陈 晖(1969-)女,湖南祁东人,硕士,华南理工大学自动化学院讲师,主要从事智能控制及最优控制的教学与研究。
摘要:模糊化是实现模糊控制的一个重要环节,针对目前文献中对模糊化方法介绍的不明确性及分散性,笔者经研究和归纳,在文中详细介绍了四种模糊化方法,指出了它们与模糊推理方法的匹配使用,并对隶属度值法进行了理论分析,给出了理论依据。关键词:模糊化;模糊控制;隶属度
Abstract:Fuzzification is an important step in the process of fuzz control. The current methods of Fuzzification introduced in many papers are not so unambiguous and complete, therefore, in this paper we introduce four methods of fuzzification in detail based on our research and consolidation, and give their applications with the approaches of fuzzy logic reasoning. The theory analyses of the membership method and theory evidence are also given in this paper.
Key words: Fuzzification; Fuzzy control; Membership
1 引言
模糊化是实现模糊控制的一个重要环节,但对其方法的研究目前还很不完善,有待于进一步探索。在有关模糊控制的文献中,对模糊化方法有的没有明确表述,有的只提到确定语言值隶属函数的方法,并没有进一步给出模糊化的方法。事实上,模糊化是将模糊控制器输入量的确定值转换为相应的模糊语言变量值的过程,而模糊语言变量值是一个模糊集合,所以模糊化方法应给出从精确量到模糊集合的转变方法。针对目前文献中对模糊化方法介绍的不明确性和分散性,笔者作了一些研究工作,总结出了四种模糊化方法。
2 模糊化方法
基本的模糊控制系统如图1所示,其中虚线框内为模糊控制器部分,模糊控制器的输入信号要经过模糊化、模糊推理及模糊判决才得到输出控制信号。在模糊控制器的设计中,模糊化的目的是为后续的模糊推理运算做准备,所以在选择模糊化方法时,除了要考虑到各模糊化方法的特点外,还应考虑到与所采用模糊推理方法的匹配问题。下面介绍的模糊化方法中的精确输入量,假设均为经过量化后的在模糊集合论域上取值的精确量。
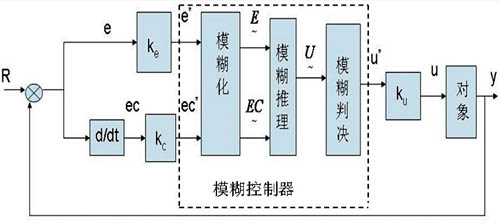
图1 基本模糊控制系统方框图2.1 分档模糊集法[1] [2] [3] [4]
分档模糊集法将模糊集合论域上的精确量分成若干档,每一档对应一个模糊集合。
例如当模糊语言值的隶属函数用表格形式表示时,如表1所示,模糊集合论域为离散整数域N={-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6},将该论域上的13个离散元素分成七档,每一档对应一个语言值。表中的七个语言值为{PB, PM, PS, O, NS, NM, NB}。
具体分档时,按隶属度最大的原则来进行,找出论域N上的元素n*与最大隶属度对应的语言值,该语言值所代表的模糊集合就是精确量n*的模糊化结果。例如表1中精确量+6模糊化为PB;+5对PB的隶属度PB(+5)为0.8,对PM的隶属度PM(+5)为0.7,
PB(+5)> PM(+5)
所以+5模糊化为PB。这样+5和+6归为一档,模糊化结果为模糊集合PB。再如n*=-3时,因为
NS()=NM()=0.7
所以-3的模糊化结果是NS或者NM。
当模糊语言值的隶属函数采用图形形式表示、论域为连续域时,也可做如上类似转换。
表1 语音值的赋值表
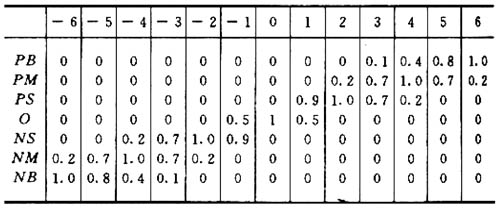
2.2 输入点隶属度取1法[5] [6] [7] [8]当模糊集合论域为离散整数域N,其上的语言值的赋值表为表1时,若输入精确量n*(n*∈N )对各语言值有隶属度为1的情况,则模糊化处理与分档模糊集法相同。例如n*=+6时,它对PB的隶属度为1,则模糊化结果为A*=PB,即
若输入精确量对各语言值没有隶属度为1的情况,则将该精确量n*处的隶属度取为1,相邻两个整数点处的隶属度取为0.5。如n*=+5时,模糊化结果为
当模糊集合论域为连续域X时,精确输入量X*(X*∈X)模糊化后的模糊集合可取常用的等腰三角形
(a) 三角形模糊集合
(b)钟形模糊集合
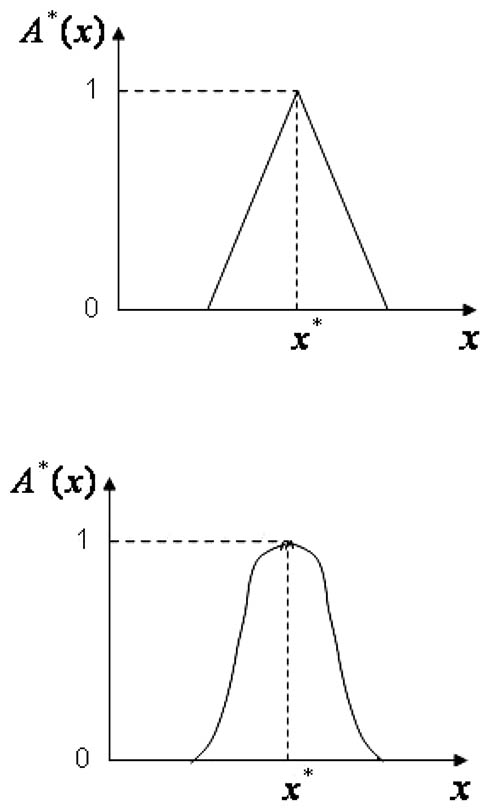
图 2 连续域时的输入点隶属度取法隶属函数,如图 2(a) 所示,在x*处的隶属度值为1。当测量数据存在随机噪声时,常采用这种方法。这时等腰三角形的顶点与该随机数的均值相对应,三角形的底边宽度是该随机数的标准差的两倍。当然三角形隶属函数并不是唯一的选择,还可选用钟形(如图2(b)所示)等其它隶属函数。
2.3 单点形模糊集合法 [1] [2] [6] [8]
将模糊集合论域X上的精确量x*模糊化为单点形模糊集合。单点形模糊集合是指该模糊集合的隶属度只在x*处为1,而在除x*以外的其余各点处都为 0 。
设A为x*模糊化后对应的模糊集合,x∈X,则
其隶属函数图形如图3所示。

图 3 单点形模糊集合的隶属函数这种模糊化方法从概念上看,已把一个精确量转换成了模糊量,但是在本质上该模糊量并没有具备模糊性,表达的仍然是确定性的信息。不过在模糊控制应用中,这种方法由于使人感到自然和易于实现而得到了广泛应用。当测量数据准确时,常常采用此法。
2.4 隶属度值法 [7] [8] [9] [10]
隶属度值法是将精确输入量对各语言值的隶属度值作为模糊化结果。因语言值的隶属函数可用离散域上的表格形式表示(如表1),也可用连续域上的解析表达式表示,所以这种模糊化方法相当于一个对应的查表或是函数计算过程。
例如在表1中,精确量-2对NS的隶属度值为1,对NM的隶属度值为0.2,而对其它语言值的隶属度为0,求出这些隶属度值即完成了对精确输入量的模糊化。
对于连续域情况,假设某语音变量的语言值{S, M, L}采用如下三角形隶属函数:
隶属函数图形如图4所示。当输入精确量为x*=6时,
M(x*)=0.8,L(x*)=0.2
则用这两个隶属度值作为x*的模糊化结果,进行下一步的模糊推理。
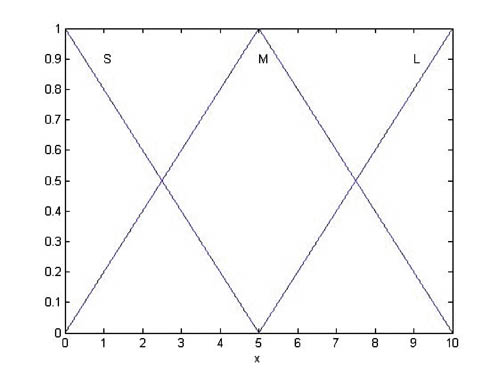
图 4 三角形隶属函数隶属度值模糊化方法主要和 Mamdani 直接模糊推理法或强度转移模糊推理法配套使用,它的模糊化结果是精确的数值而不是模糊集合,这正是上述两种模糊推理法的推理前提要求。这种模糊化方法的理论依据分析如下:
假设模糊控制规则为
If x is A Then y is B
当前输入的模糊量为单点形模糊集合A*,即
采用max-min关系合成推理法,模糊关系R由Mamdani模糊蕴涵最小运算确定,即
则推理输出B*为
可见若推理输入是单点形模糊集合,推理的结果B*可以用该输入精确量x*相对于模糊规则前件中模糊集合A的隶属度A(x*)直接对模糊规则后件中的模糊集合B进行修正(取小运算)得到。当输入模糊集合取为单点形模糊集合时,上述max-min关系合成推理法就是Mamdani直接推理法。所以Mamdani直接推理法是关系合成推理法的一个特例,它采用的模糊化方法从本质上看是单点形模糊集合法,但是为了简便直接,实际上采用的是隶属度值法。经过上述理论分析,就不难理解隶属度值法的模糊化结果不是模糊集合而是精确值了。
3 结束语
上述四种模糊化方法除隶属度值法外,模糊化结果均为一模糊集合,可用于关系合成推理法(CRI法)或特征展开近似推理法(CEI法)中,而隶属度值法主要用于 Mamdani 直接推理法或强度转移推理法中。模糊化是模糊控制器设计中的一个重要环节,但采用何种模糊化方法目前还没有完善的理论指导,设计者可根据各种模糊化方法的特点加以综合考虑。在模糊控制理论不断完善的前进道路上,模糊化方法也是其中一个值得关注的研究方向。
参考文献:
[1] 姜长生. 智能控制[M]. 北京:科学出版社,2007.
[2] 李士勇. 模糊控制神经控制和智能控制论[M]. 哈尔滨:哈尔滨工业大学出版社,1996.
[3] 章卫国, 杨向忠. 模糊控制理论与应用[M]. 西安:西北工业大学出版社,1999.
[4] 冯冬青. 模糊智能控制[M]. 北京:化学工业出版社,1998.
[5] 许力. 智能控制与智能系统[M]. 北京:机械工业出版社,2007.
[6] 李国勇. 智能控制及其 MATLAB 实现[M]. 北京:电子工业出版社,2005.
[7] 张吉礼. 模糊-神经网络控制原理与工程应用[M]. 哈尔滨:哈尔滨工业大学出版社,2004.
[8] 窦振中. 模糊逻辑控制技术及其应用[M]. 北京:北京航空航天大学出版社,1995.
[9] 罗均,谢少荣,蒋蓁. 智能控制工程及其应用实例[M]. 北京:化学工业出版社,2005.
[10] 吴晓莉,林哲辉等. MATLAB 辅助模糊系统设计[M]. 西安:西安电子科技大学出版社,2002.
[11] 诸静. 模糊控制理论与系统原理[M]. 北京:机械工业出版社,2005.
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



