当前位置:首页»案例
- 一种基于最小二乘法的摄像机非线性校正方法
-
企业: 控制网 日期: 2009-05-19 领域: 电源 点击数: 2180 
赵 阳(1980-)
女,助教,就职于河南工业职业技术学院。
摘要:摄像机线性化技术是机器视觉研究中的关键技术之一。本文针对高速彩色摄像机的非线性特性导致的图像畸变问题,分析其产生原因并给出了基于线性化校正的具体实现方法。在Visual C++6.0环境下实现了此算法,并应用异性纤维清除系统当中。试验结果表明, 该方法能够提高系统性能并有效检测皮棉中的异性纤维。
关键词:最小二乘法;非线性特性;线性校正
Abstract: The linear technology of the camera is the key technology in the research of
machine vision. In this paper, to solve picture distortion problem, we analyze the nonlinear
characteristic of the colored camera of high speed, and provide the concrete implementation
method based on that linear method of camera calibration. The algorithm have been realized
under the environment of Visual C++6.0 and applied to inspecting system for removal of the
hetero fibers..The experiment result indicates that the method improves the system
performance, and most of the hetero fibers can be detected.
Key words: least square method; nonlinear feature; correct linearly
1 引言
在基于机器视觉的光学测量设备中,物体经过光学系统(镜头)成像,通过摄像机的光电转换和扫描后,将其传入计算机,直接在计算机中处理数据并输出物体的图像。但是经常会有一些输出的图像发生畸变,这种畸变产生的原因是来自光学系统设计和制造的缺陷,或者图像传感器的失真。图像失真对基于图像的测量及检测系统的精确性会产生很大影响。因为图像处理系统需要从图像中提取物体的空间真实位置,几何尺寸及形态,当图像不含任何畸变时,可以通过对空间图像的测量与分析得到物体物理上精确的对应关系。
如果图像由于上述原因发生了畸变,则这种对应关系也发生了非线性的变化,影响图像处理系统的测量精度。在作者参与开发的异性纤维在线检测系统中图像非线性畸变严重影响了系统的清除性能,使棉产品质量不能够得到显著性的提高,所以需要对图像的非线性进行校正,使其能够以比较理想的状态来反映物像之间的对应关系。
2 摄像机成像模型与镜头非线性畸变模型
2.1 理想像机的成像模型
三维空间中的物体到像平面的投影关系即为成像模型。理想的投影成像模型是光学中的中心投影,也称为针孔模型,即假设物体表面的反射光都经过一个“针孔”而投影在像平面上,满足光的直线传播条件。图1为针孔模型成像原理图。
图1 针孔模型成像原理示意图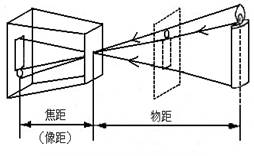
图2 理想透镜成像原理图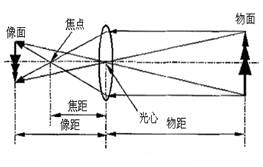
小孔成像由于透光量太小,需要很长的曝光时间,并且很难得到清晰的图像,而使用镜头可以很好地解决上述问题。因此实际摄影系统通常是由透镜或透镜组组成的。图2是理想单透镜成像原理图。在针孔成像中焦距等于像距,而在透镜成像中,焦距并不等于像距。但两者的成像关系是一致的,即像点是物点和光心的连线与图像平面的交点,所以可以用针孔模型作为摄像机成像模型。在视觉检测中摄像机的成像模型一般用理想透视成像模型来近似。
2.2 像机非线性产生原因
图3为CCD线阵像机获取图像数据的示意图。
1-像机;2-平行光源;3-物体图
图3 成像示意图
图4 相机照射背板的原始图像
由上图所知,由于物体反射光通过镜片进入CCD传感器的角度不同,即使在均匀平行光照射物体的前提下,对于同一材质且表面均匀的物体在系统上采集到的图像也是一个中间亮两端暗的图像。反映在数据曲线上基本是一个两端对称的曲线,如图4所示。
3 非线性问题的校正方法
对摄像机非线性的校正是基于图像的精确测量为基础,畸变的校正程度极大地影响测量系统的精度,从而快速、准确地对摄像机畸变进行校正是不可或缺的一步。常见的校正方法有非线性优化法、直接线性变换法等,校正前对原始图像进行噪声过滤等图像预处理,通过抑制中间信号,补偿边缘信号,从而使得像机边缘和中心处的图象信息基本类同。
3.1 最小二乘法拟合算法
从整体上考虑近似函数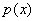 同所给数据点
同所给数据点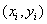 误差
误差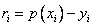
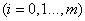 的大小,常用的方法有以下三种:
的大小,常用的方法有以下三种:
一是误差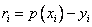
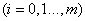 绝对值的最大值
绝对值的最大值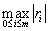 ,即误差向量
,即误差向量 的∞—范数;
的∞—范数;
二是误差绝对值的和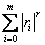 ,即误差向量
,即误差向量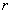 的1—范数;
的1—范数;
三是误差平方和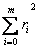 的算术平方根,即误差向量
的算术平方根,即误差向量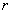 的2—范数;
的2—范数;
数据拟合的具体作法是:对给定数据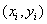
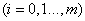 ,在取定的函数类
,在取定的函数类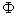 中,求
中,求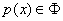 ,使误差
,使误差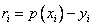
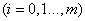 的平方和最小,即
的平方和最小,即 (1)
(1)
3.2 像机非线性参数的确定
彩色像机中有三个传感器阵列,其三个传感器阵列的非线性特性并不完全相同。下面以像机的R传感器为例,来说明获取像机校正参数的过程:
对同一材质的背板进行一次采集,原始数据为:
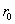 ,
,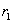 ,
,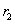 ,…,
,…,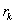 ,…,
,…, (2)
(2)
改变光强,保持其它条件不变,再一次进行图像采集并分离出R分量,得原始数据如下:
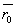 ,
,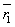 ,
,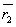 ,…,
,…,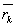 ,…,
,…,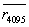 (3)
(3)
分别对两组数据进行最小二乘拟合,拟合后得到如下两组数据:
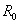 ,
,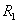 ,
,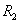 ,…,
,…, ,…,
,…,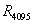 (4)
(4)
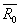 ,
,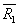 ,
,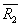 ,…,
,…,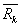 ,…,
,…,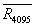 (5)
(5)
作差值运算:
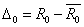 ,
,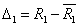 ,…,
,…,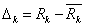 ,…,
,…,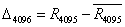 (6)
(6)
选择一标称点,在系统中我们选择中间点(第2048像素点)作为标称点,通过比例可以换算出R分量的非线性参数:(标称点的比例系数为1.0)
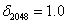 ,则其余的系数序列为:
,则其余的系数序列为:
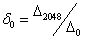 ,
,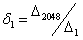 ,…,
,…,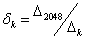 ,…,
,…,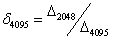 (7)
(7)
得到的数据 ,
,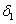 ,
,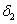 ,…,
,…,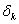 ,…,
,…,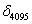 即为线阵像机R分量的非线性参数序列。同样可以得到线阵像机另外两个分量的非线性参数序列。
即为线阵像机R分量的非线性参数序列。同样可以得到线阵像机另外两个分量的非线性参数序列。
3.3 阈值上下限的提取
在系统中有三条阈值上下限,仍以R分量的上下限获取过程为例。
第一步:对标准棉花进行一次数据采集并分离出R分量,数据为:
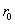 ,
,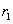 ,
,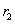 ,…,
,…,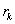 ,…,
,…, (8)
(8)
第二步:将式(8)中数据全部乘以式(7)中对应的系数并通过下面的公式:
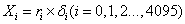 进行换算得:
进行换算得:
 ,
,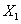 ,
,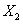 ,…,
,…,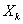 ,…,
,…,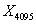 (9)
(9)
对数据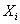 取最大值:
取最大值:
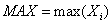 (10)
(10)
对MAX按式(7)反算可得上限序列:

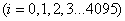 (11)
(11)
相应的下限可得到最小值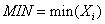 后反算即可。
后反算即可。
4 实验结果及分析
在系统调试的过程中,采用本文中的相机非线性参数整定能够有效地克服噪声以及外界环境对图象的干扰,并对图象质量进行校正,有效提高检测质量。
将(9)式中所得数据作为图象处理的基本数据,使得像机边缘部分和中间部分的图象得到一定改善,且经过实验发现基本能够满足实际要求。图5为在本系统中对数据线进行最小二乘拟合后的曲线。图像曲线较为平滑,利于数据分析及算法的优化。
图5 最小二乘法拟合后的曲线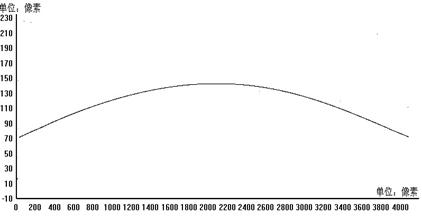
5 结束语
本文通过分析相机非线性问题的产生原因,结合数字图像的处理方法,通过标定像机参数的方法克服了由于摄像机的非线性特性所导致的像机分辨率下降以及引起的一系列问题。从现场应用来看,此方法能达到优化图像,改进异性纤维清除系统性能的要求。试验表明,最终使整机性能基本满足棉纺企业的要求。
参考文献
[1] Faig W. Calibration of close-range photogrammetric systems mathematical formulation[J]. Photogrammetic engineering& Remot Sensing, 1975,41: 1479~1486.
[2] Camera calibrationwith distortion models and accuracy evaluation-Juyang Weng, member, IEEE,Paul Cohen,and Marc Hernion.IEEE TRANSACTIONS ON PATTERN ANALYSIS
AND MACHINE INTELLIGENCE[J], VOL,14,NO.10,OCTOBER 1992.965-980.
[3] 郑南宁. 计算机视觉与模式识别[M]. 北京: 国防工业出版社, 1998.
[4] 张艳珍, 欧宗瑛. 一种新的摄像机线性标定方法[J]. 中国图像学报, 2001,6(8).
[5] 雷成, 吴福朝, 等.Kruppa方程与摄像机标定[J].自动化学报,2001,27(5).
[6] 姜大志, 等. 计算机视觉中的设备标定和三维图像重构概述[J]. 计算机工程与应用, 2001.38(13):
53-55.
[7] 丁天怀, 李勇, 苗君哲, 等. 基于BP神经网络的皮棉杂质在线检测方法[J ]. 农业工程学报, 2003, 19 (2) .
[8] 石庚尧. 浅议异性纤维在线检出装置性能特征[J]. 棉纺织技术 2004,10 612-615.
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



