- 控制系统的基本算法及软件实现
-
企业: 控制网 日期: 2009-12-16 领域: PLC&PAC 点击数: 4495 
吕卫阳
男,工学博士,副教授,现就职于北京科技大学机械工程学院机械电子工程系,主要研究方向为工业控制及自动化和先进机电系统技术。
摘 要:本文讨论了有关控制系统的基本算法及软件实现的若干问题。介绍了线性控制系统的8个典型环节,给出了这些典型环节的时间响应功能块。介绍了PID控制的基本原理及离散算法,给出了能够实现PID基本算法的功能块BasicPID,并举例说明。
关键词:典型环节;PID算法;软件实现Abstract: Some topics on the basic algorithm and software implementation of control system are discussed in this paper. The 8 essential blocks of the linear control system are introduced, and then give the function block of their time response. The basic theory and discrete method of PID control algorithm are introduced, and then give the function block BasicPID to implement the basic PID algorithm with some example.
Key words: Essential Block; PID Algorithm; Software Implementation1 控制系统典型环节的时间响应
控制系统一般由若干元件以一定的形式连接而成,这些元件的物理结构和工作原理可以是多种多样的。但是从控制理论来看,物理本质和工作原理不同的元件,可以有完全相同的数学模型,亦即具有相同的动态特性。在控制工程中,常常将具有某种确定信息传递关系的元件、元件组或元件的一部分称为一个环节,经常遇到的环节则称为典型环节。这样,任何复杂的系统总可以归结为由一些典型的环节组成,从而为建立系统模型和研究系统特性带来方便,使问题简化。
在一般情况下,线性控制系统都可以由比例环节、积分环节、微分环节、一阶惯性环节、二阶振荡环节、一阶微分环节、二阶微分环节和延迟环节等8个典型环节组成。下面分别研究这些典型环节所对应的微分方程的数值解,也即研究其时间响应的离散算法。
以下分别给出这些典型环节的时间响应离散算法的迭代公式,采用工业自动化编程标准IEC61131-3支持的ST语言在功能块中实现。
1.1 比例环节
比例环节的传递函数: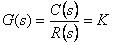
所对应的微分方程: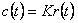
以采样周期TS进行采样,得离散化后的差分方程: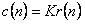
比例环节功能块ProportionalBlock如图1.1所示,其变量声明和程序代码如下所示。

图1.1 比例环节功能块ProportionalBlock
FUNCTION_BLOCK ProportionalBlock
VAR_INPUT
IN: REAL;(*输入值*)
TS: REAL;(*采样周期,秒*)
K: REAL;(*比例环节的比例常数,无量纲*)
END_VAR
VAR_OUTPUT
OUT: REAL;(*输出值*)
END_VAR
VAR
TimePeriod: TP;(*定时器*)
RisingTrigger: R_TRIG;(*触发器*)
END_VAR
(*采样周期的判断。*)
IF NOT(TS>0) THEN(*采样周期必须大于0,否则将其置为1秒。*)
TS:=1;
END_IF
(*采样周期的生成。*)
TimePeriod(IN:=NOT(TimePeriod.Q),PT:=REAL_TO_TIME(TS*1000));(*调用定时器。*)
RisingTrigger(CLK:=TimePeriod.Q);(*调用触发器。*)
(*比例环节的时间响应。*)
IF RisingTrigger.Q THEN(*在采样时刻进行迭代计算。*)
OUT:=K*IN;(*比例环节的迭代公式。*)
END_IF
1.2 积分环节
积分环节的传递函数: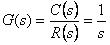
所对应的微分方程: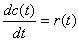
以采样周期TS进行采样,得离散化后的差分方程: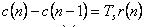
积分环节功能块IntegralBlock如图1.2所示,其变量声明和程序代码如下所示。

图1.2 积分环节功能块IntegralBlock
FUNCTION_BLOCK IntegralBlock
VAR_INPUT
IN: REAL;(*输入值*)
TS: REAL;(*采样周期,秒*)
END_VAR
VAR_OUTPUT
OUT: REAL;(*输出值*)
END_VAR
VAR
TimePeriod: TP;(*定时器*)
RisingTrigger: R_TRIG;(*触发器*)
OUT1: REAL;(*前一个采样周期的输出值*)
END_VAR
(*采样周期的判断。*)
IF NOT(TS>0) THEN(*采样周期必须大于0,否则将其置为1秒。*)
TS:=1;
END_IF
(*采样周期的生成。*)
TimePeriod(IN:=NOT(TimePeriod.Q),PT:=REAL_TO_TIME(TS*1000));(*调用定时器。*)
RisingTrigger(CLK:=TimePeriod.Q);(*调用触发器。*)
(*积分环节的时间响应。*)
IF RisingTrigger.Q THEN(*在采样时刻进行迭代计算。*)
OUT:=OUT1+IN*TS;(*积分环节的迭代公式。*)
OUT1:=OUT;(*输出值替换。*)
END_IF
1.3 微分环节
微分环节的传递函数: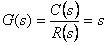
所对应的微分方程: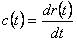
以采样周期TS进行采样,得离散化后的差分方程: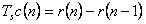
微分环节功能块DifferentialBlock如图1.3所示,其变量声明和程序代码如下所示。

图1.3 微分环节功能块DifferentialBlock
FUNCTION_BLOCK DifferentialBlock
VAR_INPUT
IN: REAL;(*输入值*)
TS: REAL;(*采样周期,秒*)
END_VAR
VAR_OUTPUT
OUT: REAL;(*输出值*)
END_VAR
VAR
TimePeriod: TP;(*定时器*)
RisingTrigger: R_TRIG;(*触发器*)
IN1: REAL;(*前一个采样周期的输入值*)
END_VAR
(*采样周期的判断。*)
IF NOT(TS>0) THEN(*采样周期必须大于0,否则将其置为1秒。*)
TS:=1;
END_IF
(*采样周期的生成。*)
TimePeriod(IN:=NOT(TimePeriod.Q),PT:=REAL_TO_TIME(TS*1000));(*调用定时器。*)
RisingTrigger(CLK:=TimePeriod.Q);(*调用触发器。*)
(*微分环节的时间响应。*)
IF RisingTrigger.Q THEN(*在采样时刻进行迭代计算。*)
OUT:=(IN-IN1)/TS;(*微分环节的迭代公式。*)
IN1:=IN;(*输入值替换。*)
END_IF
1.4 一阶惯性环节
一阶惯性环节的传递函数:
所对应的微分方程:
以采样周期TS进行采样,得离散化后的差分方程:
一阶惯性环节功能块FirstOrderLagBlock如图1.4所示,其变量声明和程序代码如下所示。
图1.4 一阶惯性环节功能块FirstOrderLagBlock
FUNCTION_BLOCK FirstOrderLagBlock
VAR_INPUT
IN: REAL;(*输入值*)
TS: REAL;(*采样周期,秒*)
T: REAL;(*一阶惯性环节的时间常数,秒*)
END_VAR
VAR_OUTPUT
OUT: REAL;(*输出值*)
END_VAR
VAR
TimePeriod: TP;(*定时器*)
RisingTrigger: R_TRIG;(*触发器*)
OUT1: REAL;(*前一个采样周期的输出值*)
END_VAR
(*采样周期的判断。*)
IF NOT(TS>0) THEN(*采样周期必须大于0,否则将其置为1秒。*)
TS:=1;
END_IF
(*采样周期的生成。*)
TimePeriod(IN:=NOT(TimePeriod.Q),PT:=REAL_TO_TIME(TS*1000));(*调用定时器。*)
RisingTrigger(CLK:=TimePeriod.Q);(*调用触发器。*)
(*一阶惯性环节的时间响应。*)
IF RisingTrigger.Q THEN(*在采样时刻进行迭代计算。*)
OUT:=(TS*IN+T*OUT1)/(T+TS);(*一阶惯性环节的迭代公式。*)
OUT1:=OUT;(*输出值替换。*)
END_IF
1.5 二阶振荡环节
二阶振荡环节的传递函数:
所对应的微分方程:
以采样周期TS进行采样,得离散化后的差分方程:
二阶振荡环节功能块SecondOrderLagBlock如图1.5所示,其变量声明和程序代码如下所示。

图1.5 二阶振荡环节功能块SecondOrderLagBlock
FUNCTION_BLOCK SecondOrderLagBlock
VAR_INPUT
IN: REAL;(*输入值*)
TS: REAL;(*采样周期,秒*)
T: REAL;(*二阶振荡环节的时间常数,秒*)
Zeta: REAL;(*二阶振荡环节的阻尼比*)
END_VAR
VAR_OUTPUT
OUT: REAL;(*输出值*)
END_VAR
VAR
TimePeriod: TP;(*定时器*)
RisingTrigger: R_TRIG;(*触发器*)
OUT1: REAL;(*前一个采样周期的输出值*)
OUT2: REAL;(*前两个采样周期的输出值*)
END_VAR
(*采样周期的判断。*)
IF NOT(TS>0) THEN(*采样周期必须大于0,否则将其置为1秒。*)
TS:=1;
END_IF
(*采样周期的生成。*)
TimePeriod(IN:=NOT(TimePeriod.Q),PT:=REAL_TO_TIME(TS*1000));(*调用定时器。*)
RisingTrigger(CLK:=TimePeriod.Q);(*调用触发器。*)
(*二阶振荡环节的时间响应。*)
IF RisingTrigger.Q THEN(*在采样时刻进行迭代计算。*)
OUT:=(TS*TS*IN+2*T*(T+Zeta*TS)*OUT1-T*T*OUT2)/(T*T+2*Zeta*T*TS+TS*TS);(*二阶振荡环节的迭代公式。*)
OUT2:=OUT1;(*输出值替换。*)
OUT1:=OUT;(*输出值替换。*)
END_IF
1.6 一阶微分环节
一阶微分环节的传递函数:
所对应的微分方程:
以采样周期TS进行采样,得离散化后的差分方程:
一阶微分环节功能块FirstOrderLeadBlock如图1.6所示,其变量声明和程序代码如下所示。

图1.6 一阶微分环节功能块FirstOrderLeadBlock
FUNCTION_BLOCK FirstOrderLeadBlock
VAR_INPUT
IN: REAL;(*输入值*)
TS: REAL;(*采样周期,秒*)
T: REAL;(*一阶微分环节的时间常数,秒*)
END_VAR
VAR_OUTPUT
OUT: REAL;(*输出值*)
END_VAR
VAR
TimePeriod: TP;(*定时器*)
RisingTrigger: R_TRIG;(*触发器*)
IN1: REAL;(*前一个采样周期的输入值*)
END_VAR
(*采样周期的判断。*)
IF NOT(TS>0) THEN(*采样周期必须大于0,否则将其置为1秒。*)
TS:=1;
END_IF
(*采样周期的生成。*)
TimePeriod(IN:=NOT(TimePeriod.Q),PT:=REAL_TO_TIME(TS*1000));(*调用定时器。*)
RisingTrigger(CLK:=TimePeriod.Q);(*调用触发器。*)
(*一阶微分环节的时间响应。*)
IF RisingTrigger.Q THEN(*在采样时刻进行迭代计算。*)
OUT:=(IN-IN1)*T/TS+IN;(*一阶微分环节的迭代公式。*)
IN1:=IN;(*输入值替换。*)
END_IF
1.7 二阶微分环节
二阶微分环节的传递函数:
所对应的微分方程:
以采样周期TS进行采样,得离散化后的差分方程:
二阶微分环节功能块SecondOrderLeadBlock如图1.7所示,其变量声明和程序代码如下所示。

图1.7 二阶微分环节功能块SecondOrderLeadBlock
FUNCTION_BLOCK SecondOrderLeadBlock
VAR_INPUT
IN: REAL;(*输入值*)
TS: REAL;(*采样周期,秒*)
T: REAL;(*二阶微分环节的时间常数,秒*)
Zeta: REAL;(*二阶微分环节的阻尼比*)
END_VAR
VAR_OUTPUT
OUT: REAL;(*输出值*)
END_VAR
VAR
TimePeriod: TP;(*定时器*)
RisingTrigger: R_TRIG;(*触发器*)
IN1: REAL;(*前一个采样周期的输入值*)
IN2: REAL;(*前两个采样周期的输入值*)
END_VAR
(*采样周期的判断。*)
IF NOT(TS>0) THEN(*采样周期必须大于0,否则将其置为1秒。*)
TS:=1;
END_IF
(*采样周期的生成。*)
TimePeriod(IN:=NOT(TimePeriod.Q),PT:=REAL_TO_TIME(TS*1000));(*调用定时器。*)
RisingTrigger(CLK:=TimePeriod.Q);(*调用触发器。*)
(*二阶微分环节的时间响应。*)
IF RisingTrigger.Q THEN(*在采样时刻进行迭代计算。*)
OUT:=(IN-2*IN1+IN2)*T*T/TS/TS+(IN-IN1)*2*Zeta*T/TS+IN;(*二阶微分环节的迭代公式。*)
IN2:=IN1;(*输入值替换。*)
IN1:=IN;(*输入值替换。*)
END_IF
1.8 延迟环节
延迟环节的传递函数:
所对应的微分方程: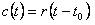
以采样周期TS进行采样,得离散化后的差分方程: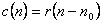
延迟环节功能块DelayBlock如图1.8所示,其变量声明和程序代码如下所示。

图1.8 延迟环节功能块DelayBlock
FUNCTION_BLOCK DelayBlock
VAR_INPUT
IN: REAL;(*输入值*)
TS: REAL;(*采样周期,秒*)
Delay: TIME;(*延迟的时间,秒*)
END_VAR
VAR_OUTPUT
OUT: REAL;(*输出值*)
END_VAR
VAR
TimePeriod: TP;(*定时器*)
RisingTrigger: R_TRIG;(*触发器*)
TONDelay: TON;(*定时器*)
END_VAR
(*采样周期的判断。*)
IF NOT(TS>0) THEN(*采样周期必须大于0,否则将其置为1秒。*)
TS:=1;
END_IF
(*采样周期的生成。*)
TimePeriod(IN:=NOT(TimePeriod.Q),PT:=REAL_TO_TIME(TS*1000));(*调用定时器。*)
RisingTrigger(CLK:=TimePeriod.Q);(*调用触发器。*)
(*延迟环节的时间响应。*)
IF RisingTrigger.Q THEN(*在采样时刻进行迭代计算。*)
TONDelay(IN := TRUE, PT := Delay);(*调用定时器。*)
IF TONDelay.Q THEN(*如果到达延迟的时间,则开始输出。*)
OUT := IN;
END_IF
END_IF
2 PID控制的基本原理及离散算法
2.1 PID控制的基本概念
PID控制是控制工程中技术成熟且应用广泛的一种控制策略。经过长期的工程实践,已经形成了一套完整的PID控制方法和典型结构,不仅适用于数学模型已知的控制系统,而且对于数学模型难以确定的工业过程也可以应用。PID控制参数整定方便,结构改变灵活,在众多工业过程控制中取得了满意的应用效果。
在闭环负反馈控制系统中,系统的偏差信号e(t)是系统进行控制的最基本的原始信号。为了提高控制系统的性能指标,可以对偏差信号e(t)进行改造,使其按照某种函数关系进行变化,形成所需要的控制规律u(t),从而使控制系统达到所要求的性能指标,即
所谓PID控制,就是对偏差信号e(t)进行“比例加积分加微分”形式的改造,形成新的控制规律u(t)。即

其中:
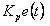 是比例控制部分,
是比例控制部分,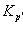 称为比例常数;
称为比例常数;
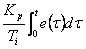 是积分控制部分,
是积分控制部分, 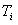 称为积分时间常数;
称为积分时间常数;
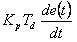 是微分控制部分,
是微分控制部分, 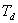 称为微分时间常数。
称为微分时间常数。
在零初始条件下,将上式两边取拉普拉斯变换,可得
基于PID控制的闭环负反馈控制系统的传递函数方块图如图2.1所示。

图2.1 基于PID控制的闭环负反馈控制系统
2.2 PID控制的离散算法
(1)位置式算法
设采样周期为T,将前述PID控制规律u(t)进行离散化处理,可得PID控制的第k个采样周期的位置式离散算法u(k)为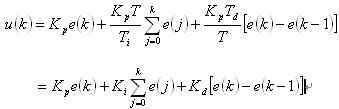
其中:
比例控制部分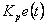 离散化为
离散化为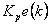 。
。
积分控制部分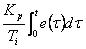 离散化为
离散化为 。令
。令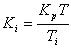 ,并称为积分控制部分的加权系数。
,并称为积分控制部分的加权系数。
微分控制部分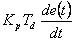 离散化为
离散化为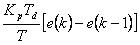 。令
。令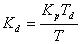 ,并称为微分控制部分的加权系数。
,并称为微分控制部分的加权系数。
(2)增量式算法
根据PID控制的位置式离散算法,可得PID控制的第k-1个采样周期的位置式输出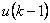 为
为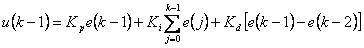
将上述两式u(k)与u(k-1)相减,可得PID控制的第k个采样周期的增量式离散算法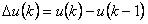 为
为
于是可得PID控制的第k个采样周期的位置式输出u(k)为

2.3 PID控制的程序实现
功能块BasicPID如图2.2所示。
在功能块BasicPID中,采用ST语言实现了PID控制的基本离散算法,其变量声明和程序代码如下所示,可以同时提供位置式输出和增量式输出。

图2.2 PID控制的基本离散算法功能块BasicPID
FUNCTION_BLOCK BasicPID
VAR_INPUT
SP: REAL; (* Setpoint/设定点 *)
PV: REAL; (* Process Variable/过程值,或称Input/输入值,或称Feedback/反馈值 *)
TS: REAL := 1; (* Sample Time/采样间隔,或称Loop Update Time/计算周期,秒 *)
KP: REAL := 1; (* ISA Dependent Gains/ISA相关增益,无量纲 *)
TI: REAL := 1; (* Integral Time/积分时间常数>0,秒 *)
TD: REAL := 0; (* Differential Time/微分时间常数>=0,秒 *)
END_VAR
VAR_OUTPUT
CV: REAL; (* Control Variable from the Current Sampling Step/当前采样周期的位置式输出值 *)
dCV: REAL; (* Delta CV or CV Change from the Current Sampling Step/当前采样周期的增量式输出值 *)
END_VAR
VAR
TimePeriod: TP; (* 定时器 *)
RisingTrigger: R_TRIG; (* 触发器 *)
ki: REAL; (* Integral Gain/积分增益系数 *)
kd: REAL; (* Differential Gain/微分增益系数 *)
ev0: REAL; (* Error Variable or System Deviation from the Current Sampling Step/当前采样周期的偏差值ev(k)=SP(k)-PV(k) *)
ev1: REAL; (* Error Variable or System Deviation from the Previous Sampling Step/前一个采样周期的偏差值ev(k-1)=SP(k-1)-PV(k-1) *)
ev2: REAL; (* Error Variable or System Deviation from the Previous before Previous Sampling Step/前两个采样周期的偏差值ev(k-2)=SP(k-2)-PV(k-2) *)
cv1: REAL; (* Control Variable from the Previous Sampling Step/前一个采样周期的位置式输出值 *)
END_VAR
(*参数的判断与计算。*)
IF NOT(TS>0) THEN(*采样周期必须大于0,否则将其置为1秒。*)
TS:=1;
END_IF
IF NOT(TI>0) THEN(*积分时间常数必须大于0,否则将其置为0,表示没有积分环节,但是应当避免被0除。*)
TI:=0;(*如果积分时间常数为负或为0,则将其置为0,表示没有积分环节。*)
ki:=0;(*此时将积分增益系数置为0,表示没有积分环节。*)
ELSE
ki:=KP/TI*TS;(*计算积分增益系数,无量纲/秒*秒=无量纲,即离散化后此系数无量纲。*)
END_IF
IF TD<0 THEN(*可以没有微积分环节,但是微分时间常数不能为负。*)
TD:=0;(*如果微分时间常数为负,则将其置为0,表示没有微分环节。*)
kd:=0;(*此时将微分增益系数置为0,表示没有微分环节。*)
ELSE
kd:=KP*TD/TS;(*计算微分增益系数,无量纲*秒/秒=无量纲,即离散化后此系数无量纲。*)
END_IF
(*采样周期的生成。*)
TimePeriod(IN:=NOT(TimePeriod.Q),PT:=REAL_TO_TIME(TS*1000));(*调用定时器。*)
RisingTrigger(CLK:=TimePeriod.Q);(*调用触发器。*)
(*PID算法的迭代过程。*)
IF RisingTrigger.Q THEN(*在采样时刻进行迭代计算。*)
ev0:=SP-PV;(*计算偏差值。*)
dCV:=KP*(ev0-ev1)+ki*ev0+kd*(ev0-2*ev1+ev2);(*当前采样周期的增量式输出值的迭代公式。*)
CV:=cv1+dCV;(*当前采样周期的位置式输出值的迭代公式。*)
ev2:=ev1;(*偏差值迭代。*)
ev1:=ev0;(*偏差值迭代。*)
cv1:=CV;(*位置式输出值迭代。*)
END_IF3 算法举例
【例1】某单位负反馈控制系统如图3.1所示,其开环传递函数为。试在PLC中编程计算其单位阶跃响应。

图3.1 单位负反馈控制系统
【解】首先将该系统的开环传递函数分解为典型环节的组合:
因此,该系统的开环传递函数由比例环节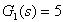 、积分环节
、积分环节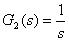 和一阶惯性环节
和一阶惯性环节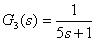 的串联所组成,其结构分解图如图3.2所示,在编程时可以分别调用上述典型环节所对应的功能块。
的串联所组成,其结构分解图如图3.2所示,在编程时可以分别调用上述典型环节所对应的功能块。
图3.2 单位负反馈控制系统的结构分解图
采用LD语言计算该系统的单位阶跃响应,变量声明如下:
PROGRAM PLC_PRG
VAR
Ts1: REAL := 0.1; (* 采样时间,秒 *)
SP1: REAL := 1; (* 设定值 *)
PV1: REAL; (* 过程值 *)
ProportionalBlock1: ProportionalBlock; (* 比例环节 *)
ProportionalBlock1OUT: REAL; (* 比例环节的输出 *)
IntegralBlock1: IntegralBlock; (* 积分环节 *)
IntegralBlock1OUT: REAL; (* 积分环节的输出 *)
FirstOrderLagBlock1: FirstOrderLagBlock; (* 一阶惯性环节 *)
FirstOrderLagBlock1OUT: REAL; (* 一阶惯性环节的输出 *)
END_VARLD如图3.3所示,单位阶跃响应曲线如图3.4所示。
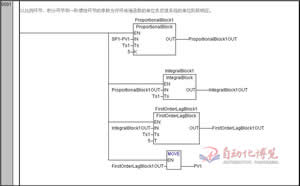
图3.3 采用LD计算单位阶跃响应

图3.4 单位阶跃响应曲线
【例2】带有PID控制器的单位负反馈控制系统如图3.5所示,已知 。试在PLC中编程计算其单位阶跃响应。
。试在PLC中编程计算其单位阶跃响应。

图3.5 带有PID控制器的单位负反馈控制系统
【解】本例与例1所述的系统基本相同,唯一不同之处是增加了PID控制器。采用CFC语言计算该系统的单位阶跃响应,变量声明如下:PROGRAM PLC_PRG
VAR
Ts1: REAL := 0.1; (* 采样时间,秒 *)
SP1: REAL := 1; (* 设定值 *)
PV1: REAL; (* 过程值 *)
BasicPID1: BasicPID; (* PID控制器 *)
KP1: REAL := 2; (* PID控制器的相关增益常数,无量纲 *)
TI1: REAL := 3; (* PID控制器的积分时间常数,秒 *)
TD1: REAL := 1; (* PID控制器的微分时间常数,秒 *)
ProportionalBlock1: ProportionalBlock; (* 比例环节 *)
IntegralBlock1: IntegralBlock; (* 积分环节 *)
FirstOrderLagBlock1: FirstOrderLagBlock; (* 一阶惯性环节 *)
END_VAR
图3.6 采用CFC计算带有PID控制器的单位阶跃响应

图3.7 带有PID控制器的单位阶跃响应曲线
CFC如图3.6所示,单位阶跃响应曲线如图3.7所示。比较图3.4和图3.7可以看出,采用PID控制后,改善了系统的综合性能。
——转自《自动化博览》
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



