|
(北京航空航天大学,北京 100191)赵治龙,祁晓野

赵治龙(1985-)男,重庆人,北京航空航天大学自动化科学与电气工程学院硕士研究生,主要研究方向为液压伺服系统设计及控制。
摘要:本文结合一弹载电液舵机系统,介绍了电液位置伺服系统的工作原理。经过推导,建立了该舵机的数学模型。在MATLAB/Simulink中搭建了舵机的仿真模型,分别对PID控制和Bang-Bang控制进行了仿真;仿真结果表明这两种控制方法无法获得满意的控制效果。为取得良好的控制效果,将PID控制和Bang-Bang控制相结合,设计了Bang-Bang+PID双模控制器,提高了系统的控制效果。
关键词:电液舵机;Bang-Bang控制;Bang-Bang+PID双模控制
Abstract: In this paper, based on a missile electro-hydraulic steering gear, the components and principle of the electro-hydraulic position servo system is introduced. The mathematical model of the steering gear is also established. PID control and Bang-Bang control of the steering gear are simulated by MATLAB software and the simulation results prove that PID control and Bang-Bang control can’t obtain satisfactory control effect. In order to get excellent control effect, Bang-Bang+PID controller is designed to obtain a better control effect than PID control and Bang-Bang control by combining them.
Key words: Electro-hydraulic steering gear; Bang-Bang control; Bang-Bang+PID control
导弹上采用的舵机类型主要有液压舵机、冷气舵机、燃气舵机和电动舵机。由于液压舵机具有体积小,功率大,响应快,负载刚度大等优点,故在弹体直径φ400mm~φ500mm左右的中高空地空导弹和近程地地导弹中应用最多。
为了适应未来战争的需要,我国从20世纪90年代初开始对正在或将要研制的导弹武器系统的技战术指标都提出了很高的要求。导弹武器系统性能的提高,相应地对导弹舵机的性能指标也提出了很高的要求,要求舵机具有控制精度高、体积小、质量轻、功率质量比大和长时间连续工作的能力。
本文将Bang-Bang控制与传统PID控制算法相结合,设计了Bang-Bang+PID控制器,较好地解决了电液舵机快速性和稳定性之间的矛盾,取得了较满意的控制效果。
1 电液舵机的组成及工作原理
本电液舵机是某导弹控制系统的执行机构,为一典型的电液位置伺服系统。舵机安装在导弹舵舱内,每个舵机驱动一个舵面,一枚导弹需用四台舵机。舵机的系统组成如图1所示。
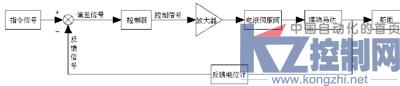
图1 电液舵机系统组成
飞控系统根据飞行器的飞行状态,发出指令信号,控制舵面偏转。指令信号和反馈信号作比较,产生偏差信号,送入舵机的控制器;控制器内预置的控制算法对偏差信号进行运算,其输出信号经过放大器之后驱动电液伺服阀;伺服阀通过电气-机械转换装置将放大器送来的电信号转变为伺服阀的阀芯位移,通过改变滑阀的开口量来调节流过伺服阀的流量进而控制摆动马达的运动,驱动舵面向消除偏差的方向运动,从而使舵面位置按照指令给定值的规律变化。
2 电液舵机数学模型的建立
2.1 放大器
放大器将输入的电压信号转变为电流信号,以驱动伺服阀。
其表达式如下:
 (1)
(1)
式中,Ka为放大器增益;Ic为控制电流。
2.2 伺服阀环节
伺服阀的线性化流量方程为:
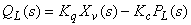 (2) (2)
式中,Kq为流量增益;Xv为伺服阀阀芯位移; Kc为伺服阀流量—压力系数:PL为负载压力。
伺服阀传递函数可用如下的二阶环节来表示:
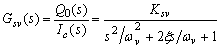 (3) (3)
式中,Q0为通过伺服阀的空载流量;Ksv为伺服阀流量增益;ωv为伺服阀固有频率;ξ为伺服阀阻尼比。
2.3 摆动马达
摆动马达流量连续性方程为:
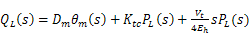 (4) (4)
式中,Dm为马达的理论平均排量;θm为马达转角;Ktc为马达的总泄漏系数;Vt为总容积;Eh为油液的等效弹性模量。
2.4 马达和负载的力平衡方程
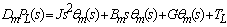 (5) (5)
式中,J为马达和负载的总惯量;Bm为粘性阻尼系数;G为负载的弹簧刚度;TL为外负载力矩。根据电液舵机各个环节的传递函数可建立如图2所示的系统方框图。
|
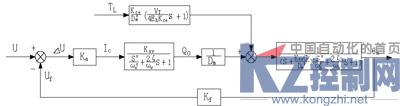
图2 电液舵机系统方框图
3 控制算法简介及仿真分析
3.1 传统PID控制
PID控制是迄今为止最常用的控制方法。传统的PID控制即比例(Proportion)、积分(Integral)、微分(Differential)控制,该算法的连续表示形式为:
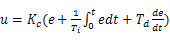 (6) (6)
式中,Kc为比例增益,e为误差,Ti为积分时间常数,Td为微分时间常数。
按照图2所示的电液舵机系统方框图,在MATLAB/Simulink环境中搭建仿真模型,将各参数带入进行仿真。在仿真进行到0.5s时加入指令信号,指令信号为使舵面偏转20o。用PID控制时系统响应曲线如图3所示。
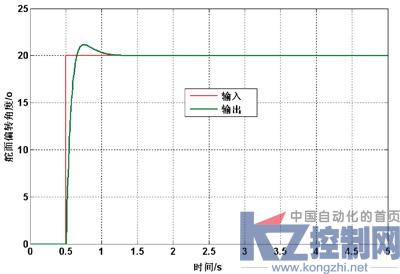
图3 PID控制响应曲线
由仿真曲线可以得到,采用PID控制时,系统反应很快,且没有稳态误差,但调节时间较长。这是因为传统PID控制采用线性定常组合方案,难于满足系统各响应阶段的要求。随着对控制性能要求的不断提高,PID控制往往不能达到满意的效果。
随着现代控制理论的发展,产生了许多以现代控制理论为基础的控制方法,应用最多的有二次型性能指标最优控制、余度控制、解耦控制、自适应控制及非连续控制中的变结构控制、PWM控制、Bang-Bang控制等控制方法[1]。
3.2 Bang-Bang控制
Bang-Bang控制的控制结构简单,可靠性高,响应时间短,是伺服控制中较有使用意义的研究方向。
Bang-Bang控制又称开关控制或最小时间控制。控制思想是以最大速度接近目标,当快到目标时,反向控制,最后以惯性接近目标。其主要任务是选择开关向量和决定切换时间。
Bang-Bang控制的最优控制律是一分段阶梯函数。

其中qj (t)为开关函数,若qj (t)只在独立的瞬间取零值,则称这种时间最优控制为平凡的[2]。
在本系统中,按如下所示的Bang-Bang控制策略对舵机进行控制:

式中,U为控制电压;e为舵面偏转角度偏差;δ为控制死区,由控制系统的精度决定。按图2所示的方框图搭建好系统模型,并给系统施加偏转20o的指令信号,采用Bang-Bang控制时的系统响应曲线如4所示。
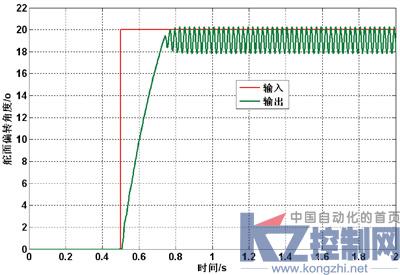
图4 Bang-Bang控制响应曲线
由仿真曲线可看出,采用Bang-Bang控制时系统出现了振荡现象。这是因为当舵面位置误差为零时,虽然控制器输出的控制电压为零,但马达的角速度不为零;由于惯性的原因,马达还会继续摆动;当偏差超过控制死区后,控制器又会输出控制信号,由此造成了系统的振荡。仿真结果表明,Bang-Bang控制在追求快速性的同时,使控制稳定性变得较差[1]。
为取得良好的控制效果,考虑将传统PID控制和Bang-Bang控制将结合,设计Bang-Bang+PID双模控制器。
3.3 Bang-Bang+ PID双模控制
Bang-Bang+ PID双模控制的控制思想即为在控制过程中采用Bang-Bang和PID两种控制方法,在大偏差范围内采用Bang-Bang控制,使系统获得较快的动态响应速度;进入小偏差范围后,采用PID控制,以减小系统的稳态误差。
Bang-Bang+PID双模控制的原理图如图5所示。
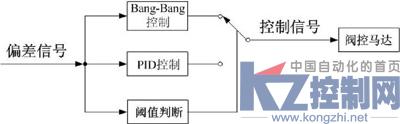
图5 Bang-Bang+ PID双模控制原理图
舵机的Bang-Bang+ PID双模控制Simulink仿真图如图6所示,响应曲线如图7所示。
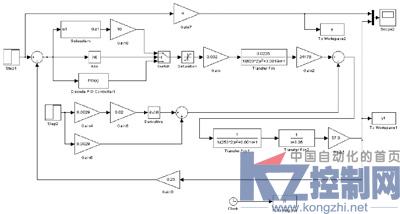
图6 Bang-Bang+ PID双模控制Simulink仿真图
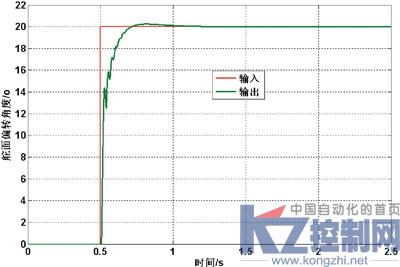
图7 Bang-Bang+ PID双模控制响应曲线
在仿真进行到5s时加入1000Nm的外干扰,以检验Bang-Bang+PID双模控制的鲁棒性,响应曲线如图8所示。
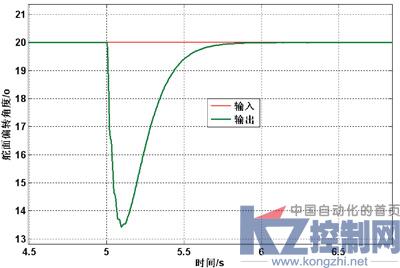
图8 加入外扰时 Bang-Bang+ PID双模控制响应曲线
为考察双模控制器对系统参数变化的敏感性,假设马达和负载的总惯量J由0.2515 Kg?m2变为0.4Kg?m2,此时系统液压固有频率ωh由252rad/s变为199rad/s,系统阻尼比由ζh由 0.12变为0.13,对比曲线如图9和图10所示。
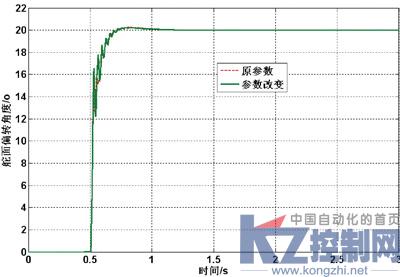
图9 参数变化时对比曲线
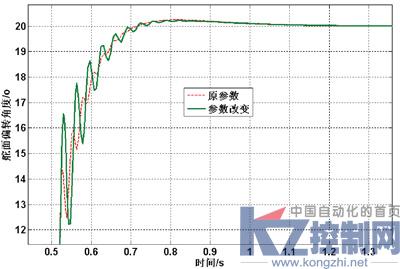
图10 参数变化时对比曲线(局部图)
分析各仿真曲线可以得到,相比于PID控制,采用Bang-Bang+ PID双模控制减少了调节时间和超调量,系统更快地进入稳定状态;当有外干扰时,采用Bang-Bang+ PID双模控制能较快地回到稳态,说明其鲁棒性较好;当系统参数发生变化时,几乎未对系统响应产生影响,故采用Bang-Bang+ PID双模控制时系统对参数变化不敏感,即适应性较好。
4 结论
电液位置伺服系统由于存在较严重的非线性、参数的时变性和外负载干扰,所以采用传统的PID控制难以取得满意的控制效果。开发和研究先进的控制策略对电液伺服控制的发展将具有重要意义。本文将传统PID控制和Bang-Bang控制相结合,设计了Bang-Bang+ PID双模控制器,改善了电液舵机系统的动态性能和稳态特性,且使系统鲁棒性和适应性较好,具有一定的参考、实用价值。
参考文献:
[1] 周向雷, 祁晓野等. 双模控制在液压非连续系统中的应用[R]. 中国航空学会飞行器控制与操纵专业委员会第十二次学术交流会, 2007.
[2] 王占林. 近代电气液压伺服控制[M]. 北京: 北京航空航天大学出版社,2005.
[3] 孟琚遐, 王渝, 王向周. 电液伺服系统Bang-Bang+Fuzzy-PID复合控制研究[J]. 机床与液压, 2009, 37, (4).
摘自《自动化博览》2010年第十期
|


 (1)
(1)
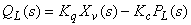 (2)
(2)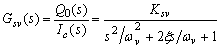 (3)
(3)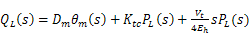 (4)
(4)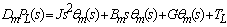 (5)
(5)
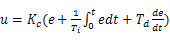 (6)
(6)




















.jpg)



