摘 要：正则路径查询的重写是实现XML查询重写优化的基础。通过比较正则路径视图和正则路径查询的结构信息，分析了两者之间进行映射应满足的条件，描述了正则路径视图到正则路径查询的映射和基于有穷自动机的映射过滤算法，并从理论上阐明了两个算法的重写等价性。借助于此两个算法，能够极大地减少需要求解的映射数目和提高正则路径查询处理的效率。

    关键词：正则路径表达式；正则路径视图；查询重写；XML

    Abstract—With the explosive increase of semi-structured data over Internet, the efficiency of XML query obtains more and more focuses. As the basic module of XML query language, the rewriting of regular path query establishes the foundation of XML query rewriting and optimizing. Based on the previous researches of query answering with multiple regular path expressions, this paper analyzed the mapping conditions that should be held between regular path view and regular path query by comparing their structural information, and described the mapping algorithm between regular path view and regular path query and the finite automata-based filtering algorithm that could eliminate those redundant and illusory mappings in all candidate mappings. At the same time, theoretic analysis showed the equivalence of original query and rewritten query using two algorithms. In addition, these two algorithms can significantly cut down the number of potential mappings and speed up the processing of regular path query.

    Keywords—regular path expression; regular path view; query rewriting; XML

    1．引言
 
    随着XML应用领域的不断扩展，越来越多的数据使用XML进行表示和交换，如何实现XML查询的重写优化相应成为查询重写优化研究的一个热点。由于多数半结构化和XML查询语言，例如Lorel[1]、Quilt[2]、XML-QL[3] 和XQuery[4]等都是基于正则路径表达式的，故对正则路径表达式的重写优化是实现XML查询重写优化的基础。

   目前，XML查询重写取得了很大进展，对XML数据检索[5]和访问控制[6]中的查询重写以及在已知XML文档模式的情况下，如何使用XML查询回答技术进行信息搜索[7]等问题都有比较深入的研究。同时，针对XML文档在Oracle数据库中的存储和查询，也有了更为成熟的成果^[8]。

    但是就正则路径表达式的重写而言，多数研究工作仍局限于单个正则路径表达式的重写[10]。由于在实际应用中，存在大量正则路径视图，而且用户查询往往含有多个正则路径表达式，这就提出了一个如何使用正则路径视图重写含有多个正则路径表达式的XML查询问题。

    2．基本概念

    一篇XML文档可以用带有根节点的标签图表示，称为XML数据图，记为G_d。其中，XML文档的元素和数据值分别用G_d的非叶子节点和叶子节点表示，元素—子元素、元素—属性及引用关系用G_d中标有相同名字的边表示。图1给出了一个XML数据图实例。形式上，设O为G_d的节点对象ID集，C为G_d的标签常量集则有如下定义^[9]：

    定义1（正则路径表达式） 正则路径表达式（regular path expression）由语法r=ε|a|_|(r₁)|r₁.r₂|r₁|’r₂|r₁*递归定义构成。其中，r、r₁和r₂均为正则路径表达式，ε表示空串，
 
                    
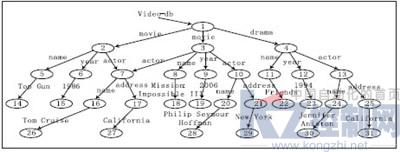
                                      图1 XML数据图实例

    a∈C表示标签常量，_表示任意一个标签。例如，r=(_*. movie).(*.actor.*.(Tom Cruise|Brad Pitt))为一个正则路径表达式，其查询结果是Gd中r能够到达的所有节点的集合。

    定义2（正则路径查询）正则路径查询（regular path query）是一种形如q(X):-y1r1z1,…,ynrnzn的查询，其中Vq={y1, z1,…,y_n,z_n}称为查询体变量，这些变量可以重复；XVq称为查询头变量，ri(1≤i≤n)是正则路径表达式。对于图1所示数据库G_d上的正则路径查询q(b):-a(movie)b,b(actor. Name."Tom Cruise")，其查询结果为π_b(q) ={2,3}。

    定义3（正则路径视图）正则路径视图（regular path view）是形如v:-y₁r₁z₁,…,y_nr_nz_n的一种查询。与正则路径查询的不同之处是视图v没有指定查询头变量，而且所含正则路径表达式ri中可以含有变量。对于图1所示数据库G_d上的正则路径视图v:-p₁(movie)p₂,p₂(year.L)p₃,p₂(actor.name. "Tom Cruise")p₄，其查询结果为π(p₁,p₂,p₃,p₄,L)={(1,2,15,26, 1986), (1,3,19,26,2006)}。

    定义4（查询树和视图树）正则路径查询q和正则路径视图v都可以用带根节点的标签图G＝(V,E,R)表示，其中V V_q为节点集，E V×D×V为有向边集，R∈V为根节点。由于q和v具有分支正则路径表达式特性，故其图表示由一个或多个无环树构成，分别称为查询树T_q和视图树T_v。图2给出了对应于式（1）的查询树Tq和视图树Tv：
   
    q(u)：-p₀r₀p₁ ，p₁r₁p₂ ，p₁r₂p₃ ，p₃r₃p₄ ， p₃r₄p₅

     v：-p₀r₅p₁ ， p₀r₆p₂

    3 查询重写

    基于视图的正则路径查询重写问题可以描述为：给定式（1）中查询q和视图v，寻找一个符号映射集以求解访问v且与q返回结果相同的查询q’。 

    3.1 符号映射

    使用正则路径视图重写正则路径查询的首要步骤是寻找T_v到T_q的符号映射（即节点映射）。其过程如下^[9]：
首先，通过广度优先搜索在T_q中寻找一个节点，使得T_v根节点能够映射到该节点；然后，标记该节点并递归寻找T_v和该节点的孩子节点间的映射；依此顺序进行下去，直到遍历完T_q中所有节点。对于T_q的一个节点w和T_v的一个节点v，如果w和v的孩子节点数分别是m和n，则在w和v之间有m!/ (m-n)!个候选映射。
很明显，在求解v到w的映射时，应满足如下条件：

    （1）v的深度≤w的深度；

    （2）v的孩子节点数≤w的孩子节点数。

    借助于该条件，可以极大地减少候选映射的数目^[9]。对于图2所示查询树和视图树，节点q0不能映射到节点p₀，因为节点q₀的孩子节点数（2）大于p₀的孩子节点数（1）。算法1首先找到能映射到根节点q₀的节点p₁和p₃，然后依次递归寻找其孩子节点间对应的子映射，最终求得候选映射集为：{{q0→p1,q1→p2,q2→p3},{q₀→p₁,q₁→p₃,q₂→p₂}, {q₀ →p₂,q₁→p₄,q₂→p₅},{q₀→p₃,q₁→p₅,q₂→p₄}}。

    算法1只是根据正则路径视图和正则路径查询的结构信息寻找到所有可能的符号映射^[9]。这些映射并非都是正确可行的，故需要验证映射中对应正则路径表达式的语言等价性。算法2使用有穷自动机实现了不等价映射的滤除[9]。由于正则路径视图中的正则路径表达式可能含有变量，所以需要对变量进行合一操作[^11]。

    对于图2中查询树T_q，使用满足L(Ai)＝L(re(ri))的有穷自动机Ai[12]替换Tq中每条标记ri的边构造成T_q；使用L(re(ri))中的任意表达式替换视图树Tv中每条标记ri的边构造成Tv，如图3所示。这里r₀=(a|b), r₁=c(d|e), r₂=c(dc)*, r₃=g|h, r₄=g, r₅=Ld|Le, r₆=(Ld)*L，其中L是标签变量。不失一般性，可以规定有穷自动机Ai有唯一的开始状态和终结状态，分别对应于边的源节点和目标节点。

                    
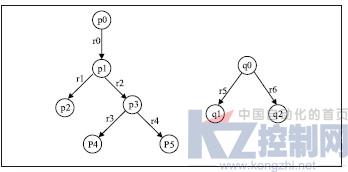
                                      图2 查询树和视图树

                   
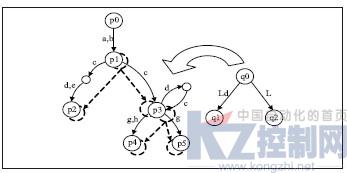
                              图3 基于有穷自动机的查询树和视图树
                  
               
              

    根据图3和算法1所找到的候选映射集，算法2能够   找到一个过滤后候选映射：{((q₀→p₁,q₁→p₂,q₂→p₃),c/L)}。这里，c/L表示c是变量L的一个替换。图3中视图和查询之间的最终映射为{((q₀→p₁,q₁→p₂,q₂→p₃),c/L)}。

    3.2 重写过程

    综上所述，使用正则路径视图重写正则路径查询的过程为：

    第一步：求解视图树到查询树的候选符号映射集П；

    第二步：验证П中候选映射的正确性和等价性，求得最终映射；

    第三步：利用最终映射对视图v进行变量替换得到v′，最后用v′重构q得到重写查询q’。

    4 算法分析

    算法1和2介绍的仅是基于单个查询树和视图树进行的，当存在多个查询树和视图树时，重复交替使用算法1和2即可解决问题。对于重写查询和原始查询的等价性问题，存在如下定理^[9]：

    定理 使用文中所给映射算法及映射过滤算法重写得到的查询q’与原始查询q的计算结果相同。

    证明：将每个子查询视为一个谓词，对于给定查询q(x,y)=p₁(x₁,…,x_i),…,p_m(y₁,…,y_j)和s(v,w)=r₁(v₁,…,v_k),…,r_n (w₁,…,w_l)，设Q₁,…,Q_m是对应于谓词p₁,…,p_m的关系表，R₁,…,R_n是对应于谓词r1,…,r_n的关系表，则查询q(u):-q(x,y),s(v,w)的计算结果为πu((Q₁⋈…⋈Q_m)⋈(R₁⋈…⋈R_n))。另一方面，假定在v中，q’(x,y)=p’( ,…, ),…, ( ,…, )， ,…, 是对应于 ,..., 的关系表，重写查询q′(u):-v,s (v,w)的计算结果为πu(( ⋈…⋈ )⋈(R₁⋈…⋈R_n))。根据文中映射算法1和2，有p_i≡ (i=1,...,m)成立，故有(Q₁⋈…⋈Q_m)＝( ⋈…⋈ )成立。所以，q′和q的计算结果相同，两者等价。

    5 结束语

    正则路径查询的重写是XML查询重写优化的一个基础问题。本文通过比较正则路径视图和正则路径查询的结构信息，分析了两者之间进行映射应满足的条件，并在此基础上描述了正则路径视图到正则路径查询的映射算法及基于有穷自动机的映射过滤算法。理论分析表明这两个算法是正确的，而且借助于这两个算法能够极大地减少需要求解的映射数目，提高正则路径查询处理的效率。

    参考文献

    [1] ABITEBOUL S, QUASS D, MCHUGH J, et al. The Lorel query language for semistructured data [J].Journal of Digital Libraries, 1997, 1(1):68-88.

    2] CHAMBERLIN D, ROBIE J, FLORESCU D. Quilt: An XML query language for heterogeneous data sources[C]. In: Suciu D, Vossen G, eds. Proc. of the Int'l Workshop on the Web and Databases. Dallas: Springer, 2000:1-25.

    [3] DEUTSCH A, FERNANDEZ M, FLORESCU D, et al. XML-QL: a query language for XML[C/OL]. World Wide Web Consortium. http://www.w3.org/TR/NOTE-xml-ql/,1998.

    [4] SCOTT B, CHAMBERLIN D, FERNANDEZ F. Mary, et al. XQuery1.0: an XML query language [EB/OL]. W3C Working Draft. http://www.w3.org/TR/xquery/, 2002. [5] MIHAJLOVI´C V, HIEMSTRA D, BLOK Ernst Henk. Vague element selection and query rewriting for XML retrieval [A]. In: Proc. of the 6th Dutch Belgian Information Retrieval workshop. Delft: Neslia Paniculata, 2006.11-18.

   [6] MOHAN S, SENGUPTA A, WU Yuqing, et al. Access control for XML-a dynamic query rewriting approach [A]. In: Proc. of the 14th ACM International Conference on Information and
Management. Bremen: ACM Press, 2005.251-252.

    [7] MANDREOLI F, MARTOGLIA R. Exploiting related digital library corpora with query rewriting[C]. In: Proc. of the 12th Italian Symposium on Advanced Database Systems. Cagliari: LITHOSgrafiche, 2004.362-369.

    [8] KRISHNAPRASAD M, LIU Zhenhua, MANIKUTTY A, et al. Query rewrite for XML in oracle XML DB[A]. In: Proc. of the 30th Conference on Very Large Data Bases. Toronto: Morgan Kaufmann, 2004.1122-1133.

    [9] Tae-Sun Chung, Hyoung-Joo Kim. A two phase optimization technique for XML queries with multiple regular path expressions[J]. Journal of Systems and Software, 2002, 64(3):183-193.

    [10] CALVANESE D, GIACOMO D, LENZERINI M, et al. Rewriting of regular expressions and regular path queries[A]. In: Proc. of the 18th ACM Symposium on Principles of Database Systems. Philadelphia: ACM Press, 1999.194-204.

    [11] 蔡自兴, 徐光佑.人工智能及其应用 (第三版)[M].北京:清华大学出版社,2004: 34-36.

    [12] 张立昂,刘田.计算理论基础(第二版)[M].北京:清华大学出版社,2000: 51-53.

    作者简介：高志军（1978），男，河北广平人，本科，现就职于邢台金牛玻纤有限责任公司生产部，主要从事企业信息化建设方面的研究。

    摘自《自动化博览》2011年第五期