当前位置:首页»企业
- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 基于遗传算法优化模糊神经网络的倒立摆智能控制 技术领域 仪器仪表 行业 简介 内容  王猛(1984- ),男,辽宁工业大学研究生,(辽宁工业大学信息科学与工程学院,辽宁 锦州 121001) 研究方向:智能控制。
王猛(1984- ),男,辽宁工业大学研究生,(辽宁工业大学信息科学与工程学院,辽宁 锦州 121001) 研究方向:智能控制。
基金项目:辽宁省博士启动基金项目(项目号:20071096)。
摘要:提出了一种利用遗传算法来优化模糊神经网络的倒立摆智能控制, 利用RBF神经网络与模糊推理过程具有函数等价性, 设计了基于模糊系统的RBF网络结构。同时采用改进的遗传算法优化了神经网络的参数和权值。其中利用一种动态的交叉率和变异率,有效地加快了收敛的速度。最后,利用Matlab软件对倒立摆进行仿真,仿真结果表明,该控制具有较好的通用性和控制效果。
关键词:遗传算法;RBF神经网络;动态的交叉率和变异率;仿真
Abstract: One type of intellectual control of the inverted pendulum which is using genetic algorithm to optimize fuzzy-neural network is presented in this paper. The RBF network structure based on fuzzy system is designed by functional equivalence between RBF neural network and fuzzy reasoning process. Simultaneously, the parameters and weights of neural network are optimized by utilizing the improved genetic algorithm. The speed of convergence is improved efficiently by using dynamic crossover and mutation. Finally, the inverted pendulum is simulated by Matlab. The simulation results show its effectiveness and availability.
Key words: Genetic Algorithm; RBF Neural Network; Dynamic Crossover and Mutation; Simulation
神经网络是对生物神经网络系统的模拟,它具有并行计算、分布式信息存储、容错能力强以及联想记忆功能,同时还具有较强的自适应、自学习能力等一系列的优点,因此神经网络的研究受到广大学者的关注。另一方面,模糊系统具有能处理不确定性、非线性等问题的能力,其推理方式类似于人类的思维方式。上述两者具有很好的互补性,其相互结合构成的控制具有很强的自适应能力。
遗传算法(GA)作为一种基于自然遗传学机理的优化方法,通过采用随机但有向的搜索机制来寻找全局最优解。采用遗传算法来训练神经网络可以实现结构和参数的快速、全局寻优。模糊系统、神经网络和遗传算法被认为21世纪人工智能界最具有发展前途的三个重要领域,它们构成了所谓的智能计算或称软计算。
本文设计了一种基于改进遗传算法的模糊神经网络对倒立摆的控制。其网络结构是基于径向基函数的神经网络,并利用GA对所有的高斯型隶属函数和权值进行了优化。该控制的优点在于结构简单,实现了自学习、自适应控制。
1模糊神经网络的设计
RBF神经网络是在借鉴生物局部调节和交叠接受区域知识的基础上提出的一种采用局部接受域来执行函数映射的人工神经网络。跟传统的BP网络相比,其优势在于学习过程收敛速度快,网络连接权值与输出呈线性关系,具有唯一最佳逼近的特性,并且不存在陷入局部最优的问题。更为重要的是,采用RBF设计模糊神经网络的最大优势在于RBF网络与模糊推理过程具有函数等价性,这个等价性将两种不同构造的系统在函数上统一起来,使网络的参数和运算有了明确的物理意义。文中设计了一种基于模糊神经网络的RBF网络结构如图1所示。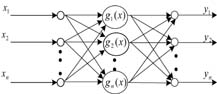
图1 RBF网络结构
其中,RBF神经网络是一个三层前向输出网络,输入层与隐层直接连接。输入层的输入变量为系统的状态反馈量,其中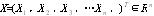 是一个输入样本向量。把输入变量分为7个模糊子集,分别为正大(PB)、正中(PM)、正小(PS)、零(ZERO)、负小(NS)、负中(NM)、负大(NB)。模糊推理过程在隐层进行。则第i个隐层节点的激发函数g (X)为以下的公式:
是一个输入样本向量。把输入变量分为7个模糊子集,分别为正大(PB)、正中(PM)、正小(PS)、零(ZERO)、负小(NS)、负中(NM)、负大(NB)。模糊推理过程在隐层进行。则第i个隐层节点的激发函数g (X)为以下的公式: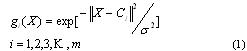
其中m是隐含层节点个数;C 为第i个基函数的中心向量,其元素个数与X相同, 是一个数量值,它决定了该基函数围绕中心的宽度。 是向量 的欧氏范数,它表示X和C 之间的距离,采用2-范数进行计算。g (X)在C 处有唯一的最大值,随着 的增大,g (X)迅速衰减到零,对于给定的输入X,只有一小部分靠近X的中心被激活。
每个模糊规则的控制强度则由隐层和输出层的权值给出。RBF结构用模糊控制规则可表示为:
IF
其中,W 是对应于第m个输出变量的第i个控制规则的权值。
输出层则是控制对象的控制信号( Y ……Y )。从隐层到输出层是线性映射,对于第m个输出变量Y ,可按以下公式计算:
根据上述三式,很容易看出,每个RBF网络的隐元按照一个径向对称函数计算其输出,输入离隐元的中心越近,获得的输出也越大。
2基于改进遗传算法的设计
2.1遗传算法简介
遗传算法是由Holland教授提出的模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法,是一种宏观意义下的仿生算法。其对于多变量、目标函数不可微或不确定问题解的寻优,比传统的优化方法有着更广泛的适应性。由于遗传算法在搜索时不依赖于梯度信息,这就使得它可以高效率地发现全局最优解或接近最优解,因此非常适合于对模糊控制隶属函数的调节和神经网络权值的优化。
GA的基本操作算子有三个:选择(selection)、交叉(crossover)和变异(mutation)。选择即从当前群体中选择适应值高的个体以生成交配池(mating pool)的过程。通常采用的方法有轮盘赌法、联赛选择、排序选择。交叉是把两个父代个体的部分结构加以替换重组而生成新个体的操作。一般有一点交叉、两点交叉和多点交叉这三种。变异是模拟自然界生物体进化中染色体上某位基因发生的突变现象,从而改变染色体的结构和物理性状。
2.2利用遗传算法对倒立摆控制寻优的主要步骤
2.2.1倒立摆参数的编码策略
仿真的控制对象为一级倒立摆模型,设计一个两输入,单输出的控制系统。输入变量为小车的位置误差跟小车摆角的误差,输出为小车的控制力。高斯型隶属函数输入变量分为7个模糊子集,而每一个高斯隶属函数的输入都有中心和宽度两个参数,因此总共有2×2×7=28个参数。模糊控制规则数为49,取隐层神经元个数等于模糊控制规则个数,则相应有49个隐层神经元个数,即需49个权值W 用来连接隐层单元到输出节点,假设为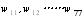 。这样,共有77个参数和权值需要用GA来优化。针对优化的参数个数,选用的编码方式为实数编码。编码时先把不同的中心与之对应的宽度顺序排列完后再顺序排列各个调节权值,这样做的好处是在交叉算子作用下,中心和宽度在一个个体上同时变化的概率较高,容易实现中心变化时宽度也随之变化的要求。
。这样,共有77个参数和权值需要用GA来优化。针对优化的参数个数,选用的编码方式为实数编码。编码时先把不同的中心与之对应的宽度顺序排列完后再顺序排列各个调节权值,这样做的好处是在交叉算子作用下,中心和宽度在一个个体上同时变化的概率较高,容易实现中心变化时宽度也随之变化的要求。
2.2.2遗传算法的参数寻优过程
在寻优过程的开始,初始种群包含了分布于整个搜索空间的一些染色体。在仿真中,随机产生60个染色体作为初始种群。在每一个染色体被评估和分配了适应值之后,当前的种群开始进行选择,来产生下一代种群。采用轮盘赌法来决定新种群的个数。在新种群建立之后,交配池形成,而后进行交叉、变异。每产生一代种群,评估、选择、交叉、变异都要被进行,直到最终条件被满足。
采用二点交叉法进行交叉,而且不同于一些论文中采用的自适应交叉率和变异率,而是采用了一种动态的交叉率和变异率,如图2所示。并且,还利用最优保留策略进行选择操作,即让具有最好适应值的前3个染色体直接复制到下一代。采用上述的方法作用可以使种群更快的收敛。对于适应度函数的选择,按照下式进行:
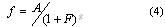
其中,f为适应度,F为目标函数,g是影响性能曲线的一个常量,A是一非负常量,它须较合理的选择,以免f太小。其中,N为当前迭代数,M为最大迭代数。
图2 动态的交叉率和变异率
3仿真
倒立摆作为一个实验装置,是一个高阶次、不稳定、多变量、非线性的系统,具有形象直观、结构简单、构件组成参数和形状易于改变等特点。对倒立摆的研究可归结为对非线性、多变量、绝对不稳定系统的研究,它在控制过程中能有效地反映控制中的许多关键问题,如非线性问题、系统的鲁棒性问题、随动问题、镇定问题及跟踪问题等。因此对倒置系统的研究具有深远的意义。
倒立摆系统的小车可自由地向左或向右运动,同时摆可在垂直平面内自由运动。该系统的动力学方程为:
在仿真时,重力加速度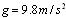 ,小车质量
,小车质量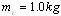 ,杆的质量
,杆的质量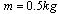 ,半长
,半长 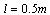 ,u为作用在小车上的控制力,忽略所有的摩擦力。控制过程为给定小车一个初始状态,其值分别为:
,u为作用在小车上的控制力,忽略所有的摩擦力。控制过程为给定小车一个初始状态,其值分别为: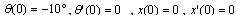 控制力u在[-6,+6]上连续取值,然后控制小车在尽量短的时间内回到中心,并且摆角为垂直。其仿真如图4和图5所示,控制效果令人满意。
控制力u在[-6,+6]上连续取值,然后控制小车在尽量短的时间内回到中心,并且摆角为垂直。其仿真如图4和图5所示,控制效果令人满意。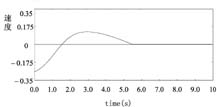
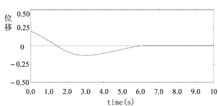 图3 小车的速度和位移示意图
图3 小车的速度和位移示意图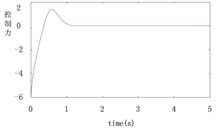 图4 小车的控制力示意图
图4 小车的控制力示意图
4 结论
利用RBF神经网络的自学习和逼近任意函数的能力以及其等价于模糊推理的特性,设计了基于遗传的模糊神经网络对倒立摆控制,并采用具有动态交叉率和变异率的遗传算法来优化神经网络的参数和权值。仿真结果表明,基于动态遗传算法的模糊神经网络有一定的通用性和较好的控制效果。
参考文献
[1] Siddique M. N. H, Tokhi M. O. GA-based neuro-fuzzy logic controller for flexible-link manipulator[J]. IEEE, 2002,(9).
[2] Ovidiu Popvoci Vlad, Toshio Fukuda. Neuro-fuzzy motion controller design using improved simple genetic algorithm[J]. IEEE, 2003, (7).
[3] 王学雷,邵惠鹤,李亚芬.一种径向基函数神经网络在线训练算法及其在非线性控制中的应用[J].信息与控制,2001,(6): 249-253.
[4] 张智星,孙春在,水谷英二[日].神经-模糊和软计算[M].西安:西安交通大学出版社,2002.
[5] 丛爽.径向基函数网络的功能分析与应用的研究[J].计算机工程与应用,2002,(3):85-87.
[6] 杨国军,崔平远,李琳琳.遗传算法在神经网络控制中的应用与实现[J].系统仿真学报,2001,(9): 567-570.
[7] 李国勇.智能控制及其MATLAB实现[M].北京:电子工业出版社,2005.
[8] 韩敏,孙燕楠,许士国.一种模糊逻辑推理神经网络的结构及算法设计[J].控制与决策, 2006(21):415-416.
其他作者:
王艳秋(1955-),女,教授,辽宁工业大学信息科学与工程学院院长,博士,硕士研究生导师,研究方向:近代交流调速系统;智能控制。





.jpg)




