- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 线性广义时滞系统的状态反馈H∞控制 技术领域 人机界面 行业 简介 内容  廖勇(1982—)
廖勇(1982—)
男,江西抚州人,硕士研究生,主要研究方向为广义系统的鲁棒控制。
摘要:首先利用线性矩阵不等式(LMI)方法,给出线性广义时滞系统稳定的一个充分条件;然后讨论广义时滞系统的H∞状态反馈控制,给出控制器存在的充分条件,同时给出控制器的设计,控制器可由矩阵不等式解得。
关键词:广义时滞系统;线性矩阵不等式;H∞控制Abstract: Using the method of linear matrix inequality (LMI),H∞ state feedback control problem for linear singular systems with time-delay in state is discussed. A sufficient condition which guarantees the asymptotical stability of the closed-loop system is given. Furthermore, one sufficient condition for the existence of an H∞ state feedback controller is shown. The controller can be obtained via solving matrix inequality.
Key words:Singular time-delay system; LMI; H∞ control
为适应近代科学技术的发展以及大型工程技术的需要,人们提出了非传统数学模型描述的广义系统。信息传递等因素致使系统普遍存在滞后现象[1,2],因而人们又提出滞后广义系统[3,4]。滞后广义系统的结构相当复杂[4],既不同于无滞后的广义系统,又不同于通常的滞后系统。
H∞控制理论是鲁棒理论的一个重要分支,近年来随着无滞后线性系统H∞理论的日趋成熟和完善,滞后线性系统的H∞理论也得到了相应的发展[5,6]。但由于广义滞后系统结构的复杂性,致使对滞后广义系统的H∞控制问题的研究仍处于初级阶段[4]。本文利用线性矩阵不等式方法,讨论一般的广义时滞系统H∞控制问题,给出了问题可解的一个充分条件以及控制器设计。
1 问题描述与预备知识
考虑如下线性广义时滞系统
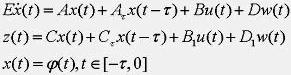 (1)
(1)其中:
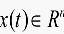 为系统的状态变量,
为系统的状态变量,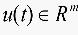 为控制输入,
为控制输入,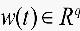 为干扰输入,
为干扰输入,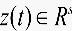 为控制输出,
为控制输出,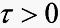 为滞后常数,
为滞后常数,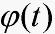 为任一连续的满足相容性条件的初始函数,各系数矩阵为适维常阵。特别地,
为任一连续的满足相容性条件的初始函数,各系数矩阵为适维常阵。特别地,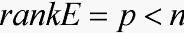 。不失一般性,假设
。不失一般性,假设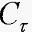 ,Bl和Dl都为零矩阵,否则可通过状态扩维方式将系统(1)转化为
,Bl和Dl都为零矩阵,否则可通过状态扩维方式将系统(1)转化为
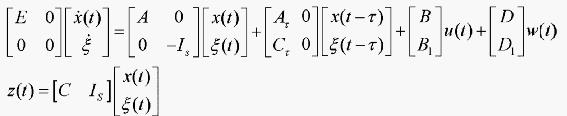
本文的目的是设计无记忆的状态反馈
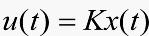 (2)
(2)
其中 为常阵,使得系统(1)与反馈控制器(2)构成的闭环系统
为常阵,使得系统(1)与反馈控制器(2)构成的闭环系统
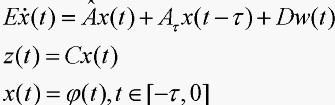 (3)
(3)
满足如下条件:1)内稳定;2)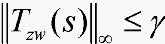 ,其中:
,其中: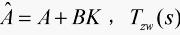 表示从干扰输入W(t)到被控输出Z(t)的传递函数,
表示从干扰输入W(t)到被控输出Z(t)的传递函数,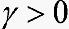 为给定常数。
为给定常数。
设有滞后广义系统
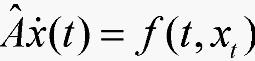 (4)
(4)
其中: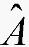 为n×n奇异常数矩阵,
为n×n奇异常数矩阵,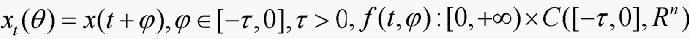
且连续,
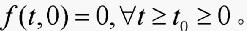
方程(4)的初始条件为
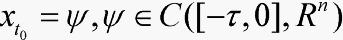 (5)
(5)
在给出稳定性概念之前,还需引用如下记号:
1) 区间Tk=[0,tk),其中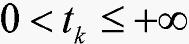 ;
;
2) m维连续可微向量函数q(t,x)在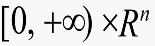 上有定义;
上有定义;
3) sk(t0,tk)为使得方程(4)至少在[t0,tk)上有连续解的所有相容初始函数的全体;
4) 。
。
定义1[7]若 ,总存在
,总存在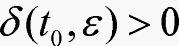 ,使得
,使得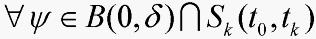 ,方程(4)通过初始条件
,方程(4)通过初始条件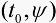 的解
的解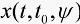 满足
满足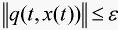 和
和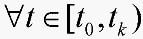 ,则方程(4)的零解关于
,则方程(4)的零解关于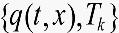 稳定。
稳定。
特别地,若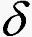 仅与
仅与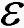 有关,而与t0无关,则方程(4)的零解关于{q(t,x),Tk}一致稳定。
有关,而与t0无关,则方程(4)的零解关于{q(t,x),Tk}一致稳定。
定义2[7]若方程(4)的零解关于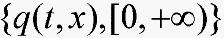 是稳定的,且
是稳定的,且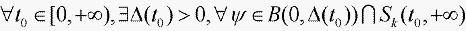 ,有
,有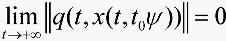 则称方程(4)的零解关于
则称方程(4)的零解关于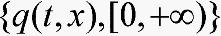 渐近稳定。
渐近稳定。
引理1[8]给定矩阵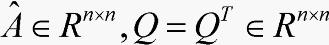 ,若
,若 ,且
,且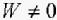 , 则
, 则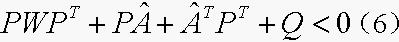 可 行 当 且 仅 当
可 行 当 且 仅 当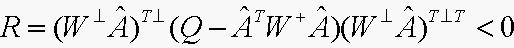 , 若(6)可 行, 记
, 若(6)可 行, 记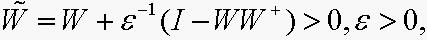 则(6)的所有可行解为
则(6)的所有可行解为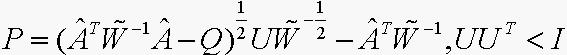 其中,
其中,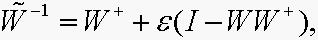
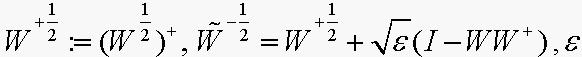 满足,
满足,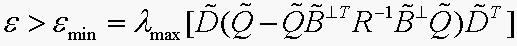 ,其中,
,其中,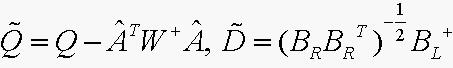 ,
,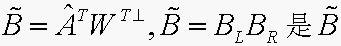 的一个满秩分解。
的一个满秩分解。
引理2[9]若存在矩阵 和正定阵
和正定阵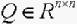 满足
满足
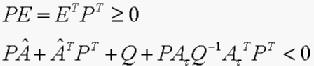 (7)
(7)
则系统(3)零解渐近稳定。
引理 3[9] 若存在矩阵 和正定阵
和正定阵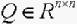 满足
满足
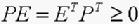
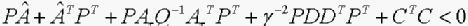 (8)
(8)
则闭环系统(3)内稳定且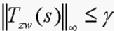 。
。
引理4[9]若存在矩阵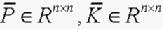 ,和正定矩阵
,和正定矩阵 满足如下LMI不等式
满足如下LMI不等式
 (9)
(9)
其中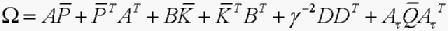 ,则系统(1)的H∞控制问题有解,即系统(3)内稳定,且满足H∞范数界
,则系统(1)的H∞控制问题有解,即系统(3)内稳定,且满足H∞范数界 。此时控制器
。此时控制器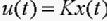 ,其中
,其中 。
。
2 主要结果
定理1 若存在矩阵 和正定阵
和正定阵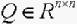 满足
满足
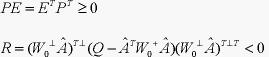
则系统(3)零解渐近稳定。
其中,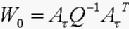 。
。
证明 引理2中(7)的第二个不等式等价于下式
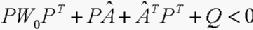
则将引理1的结果应用于引理2即可得定理1。
下面给出系统(3)内稳定且满足H∞范数界,即 的一个充分条件。
的一个充分条件。
定理2 若存在矩阵 和正定阵
和正定阵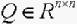 满足
满足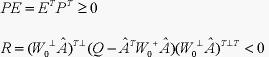
则闭环系统(3)内稳定且 。
。
其中,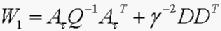 ,而且所有的矩阵P满足以下两式:
,而且所有的矩阵P满足以下两式:
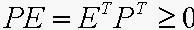 (10)
(10)
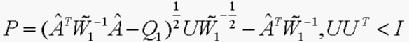 (11)
(11)
其中,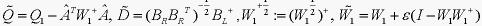 ,
,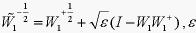 满足,
满足,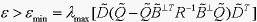 ,其中,
,其中,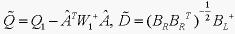 ,
, 是
是 的一个满秩分解。
的一个满秩分解。
证明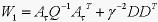 ,因为正定,所以
,因为正定,所以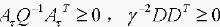 ,则
,则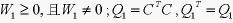 。将引理1中的结果应用到引理3即可证明定理2(证明略)。
。将引理1中的结果应用到引理3即可证明定理2(证明略)。
定理3 若存在矩阵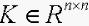 ,和正定矩阵
,和正定矩阵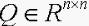 满足如下矩阵不等式
满足如下矩阵不等式
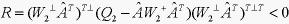 (12)
(12)
其中,,则系统(1)的H∞控制问题有解,即系统(3)内稳定,且满足H∞范数界 。
。
证明 使用两次Schur补引理可将(8)式简化成下列不等式
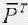 (Q+CTC)
(Q+CTC) +(A+BK)
+(A+BK) +
+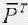 (A+BK)T+
(A+BK)T+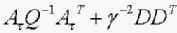 <0
<0
将引理1的结果应用到引理4即可得定理3。参考文献:
[1]Hale J K. Theory of Functional Differential Equations[M].New York:Springer Verlag,1977.
[2]刘永清,唐功友.大型动力系统的理论与应用——卷三:滞后、稳定与控制[M].广州:华南理工大学出版社,1992.
[3]Campbell S L. Singular Systems of Differential Equation[M].San Francisco:
Pitman,1980.
[4]刘永清,谢湘生.大型动力系统的理论与应用——卷八:滞后广义系统的稳定,镇定与控制[M].广州:华南理工大学出版社,1998.
[5]Wen T, Yaling C. H∞-optimal control for descriptor systems[A]. Proc of 12th IFAC World Congress[C].Sydney,1993.2:201-204.
[6]Masubuchi I,Kamitane Y,Ohara A,et al. H∞ control for descriptor systems:A matrix inequalities approach[J].Automatica,1997,33(1):669-673.
[7]刘永清,王伟,李远清.大型动力系统的理论与应用——卷七:滞后广义系统解的基本理论与应用[M].广州:华南理工大学出版社,1997.
[8]曾建平,张怡,车玲.一类线性矩阵不等式可行解集的构造.Proceedings of the 24th Chinese Control Conference[C].Guangzhou,P.R.China,2005.7:538-540.
[9]冯俊娥,程兆林.线性广义时滞系统的H∞状态反馈控制器[J].控制与决策,2003,18(2):159-163.
(厦门大学自动化系,福建 厦门 361005) 廖 勇,曾建平





.jpg)




