- 企业简介
-
艾默生(美国纽约证券交易所代码: EMR)是一家全球性的技术与工程公司,为工业、商业及住宅市场客户提供创新性解决方案。自动化解决方案业务帮助过程、混合和离散行业制造商优化其能效和运营成本,促进生产,确保人员安全和保护环境。商住解决方案帮助确保人类舒适度和健康,保障食品质量和安全,提升能效,打造可持续发展的基础设施。如欲了解更多信息,欢迎访问:www.emerson.cn。
- 公司类型:供应商
- 联系方式
-
- 艾默生
- 地址:上海市浦东新区新金桥路1277号
- 邮编:201206
- 电话:021-2892 9000
- 传真:021-2892 9001
- 网址:http://www.emerson.cn
- Email:China.info@emerson.com
- 联系人:市场部
- 案例详细
-
标题 基于免疫遗传算法优化的模糊神经元网络控制器在全阶精馏塔模型中的控制仿真研究 技术领域 仪器仪表 行业 简介 内容 摘要:提出了一种免疫遗传算法优化的模糊控制器,利用免疫遗传算法的全局搜索功能和神经元的自学习能力,提高了模糊控制器的控制精度和抗干扰能力。将该控制器用于全阶精馏塔模型仿真,仿真结果表明该控制器可以有效地消除静态误差,并在控制的过渡过程也有很好的鲁棒性,实际应用效果也表明了该方法的优越性。
关键词:免疫遗传算法;模糊;精馏塔
中图分类号:TP273
Abstract: A fuzzy controller optimized by immune genetic algorithm (IGA). By utilizing the global search ability of immune genetic algorithm(IGA) and self-learning ability of neuron controller, the new approach increases the control accuracy of fuzzy controller and improves its ability of anti-interference. The simulation result, which was obtained by applying the method to full order rectification column model, shows static error was effectively reduced and the robustness of the new approach in controlling shock in the process was satisfactory. Also, the advantages of this new approach are shown in practical applications.
Keywords: Immune genetic algorithm; Fuzzy; Rectification Column
1 引 言
精馏是炼油、化工生产中应用最为广泛的传质传热过程。精馏塔不仅模型难以建立而且控制方案复杂。许多学者在精馏塔的模型建立和控制仿真上做了大量的研究并取得了良好的效果。本文设计了一种免疫遗传算法优化的模糊控制器对基于奇异摄动法降阶的精馏塔模型进行控制仿真研究。结果表明,这种控制器的控制效果在控制精度和过渡过程的效果上都表现出良好的效果。
2 控制算法
精馏塔最直接的质量指标是产品纯度。过去由于检测上的困难,难以直接按产品的纯度进行控制。现在随着分析仪表的发展,特别是工业色谱仪的在线应用,已逐渐出现直接按产品纯度来控制的控制方案。
直接按产品纯度的控制方案的好处在于:直接可以控制产品的质量。但是这种控制的难点在于被控变量的可调范围小(只能在0~1区间变化)。根据这种现实情况,本文设计了一种免疫微粒群算法调节增益的模糊控制器。其具体的算法如下:
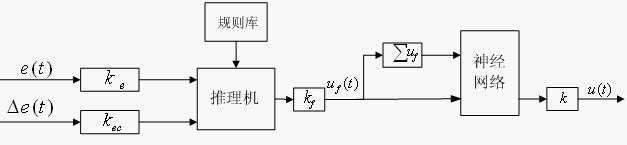
图1 模糊-神经元结构使用公式法的模糊推理方法:
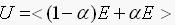 (1)
(1)
式中,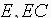 分别是系统偏差
分别是系统偏差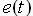 和偏差变化量
和偏差变化量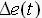 的模糊量;
的模糊量;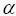 是模糊规则的调整因子,通过调整
是模糊规则的调整因子,通过调整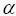 可以修改规则。U是系统的模糊输出。公式法模糊控制算法如下:
可以修改规则。U是系统的模糊输出。公式法模糊控制算法如下:
模糊法:
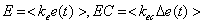 (2)
(2)
模糊推理:
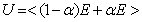 (3)
(3)
反模糊化:
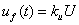 (4)
(4)
式中,Ke、Kec分别是模糊控制系统输入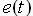 和
和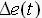 的模糊化比例因子,其取值可以根据精确量的范围和划分区域来确定。<x>表示一个与x同号,绝对值四舍五入的整数。U是系统的模糊输出。模糊规则的调节因子
的模糊化比例因子,其取值可以根据精确量的范围和划分区域来确定。<x>表示一个与x同号,绝对值四舍五入的整数。U是系统的模糊输出。模糊规则的调节因子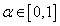 。Ku是解模糊因子,
。Ku是解模糊因子,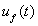 是模糊控制器的输出,将它作为神经元增益的变化量。即:
是模糊控制器的输出,将它作为神经元增益的变化量。即:
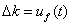 (5)
(5)
神经网络算法:

图2 带有非线性激励函数的单神经元权函数的选取:
在大多数的情况下,权函数的优化是由反复试验和修正来选定的。这就是神经网络应用的限制所在,在权函数的优化研究上有大量的工作,Yamada和Yabuta基于最速下降法提出了一种自整定方法,并且用仿真试验论证了这种方法的特点和实用性。
权函数定义为:
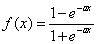 (6)
(6)
其中x是神经网络输出,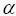 是可以定义动态函数的形状。
是可以定义动态函数的形状。
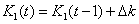 (7)
(7)
当设定值r(t)突然变小(大)时,由于误差和误差变化量的变化使得 也相应突然变小(大),会使控制器的输出有可能产生超调或反调,本文在增益自整定算法中引入
也相应突然变小(大),会使控制器的输出有可能产生超调或反调,本文在增益自整定算法中引入 项,它的变化方向和设定值的变化方向相反,通过适当地将K(t)值提高(降低),达到有效地抑制超调或反调量。则有:
项,它的变化方向和设定值的变化方向相反,通过适当地将K(t)值提高(降低),达到有效地抑制超调或反调量。则有:
 (8)
(8)
式中,K1为一常数,K0为增益的初始值。
免疫遗传算法(IGA):
人工免疫系统是从自然免疫系统中抽象出来的,是目前在人工智能领域研究的热点问题之一[86]。免疫系统具有辨识能力,能够排除外来的抗原和胚细胞等异物。同时免疫系统还具有类似模式识别中记忆能力和学习能力。在免疫系统中,有一种反馈机制能同时执行两项不同的工作;一是外部物质的出现应答,二是快速稳定免疫系统。根据免疫系统的反馈机制,可以抽取如下的免疫反馈规律。生物免疫系统抗体多样性的遗传机理和细胞选择机理对于改进和提高遗传算法的能力具有重要的启迪作用[1] : 抗体的多样性对于提高遗传算法(IGA)的全局搜索能力同时保证不陷于局部最优解,同时自我调节机构可提高遗传算法(IGA)的局部搜索能力,并且免疫记忆功能可以加快搜索速度,提高遗传算法的总体搜索能力[2] 。具体的说就是用两个免疫操作来优化遗传算法:①抵抗②免疫选择[3]。
抵抗:假设个体x,抗体操作的意思是基于先前的信息在某些位上修改基因来最大可能的获得高的适应度。假设一个群体为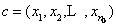 ,在C上的抗体操作即是
,在C上的抗体操作即是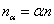 个体是从先前知识按比例
个体是从先前知识按比例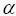 选择从来的。这个操作的数量和有效性在IGA中有着重要的角色。
选择从来的。这个操作的数量和有效性在IGA中有着重要的角色。
免疫选择:先是检查抗生物,如果比父辈的适应度小,则表示在交叉变异时出现了严重的基因损坏,这样就将父辈来进行下一次竞争。然后是退火选择[4]:从先前的后代中选择个体时引入概率: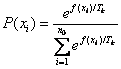 其中:
其中: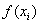 是个体
是个体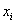 的适应度,
的适应度,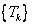 是温度控制序列趋于0。
是温度控制序列趋于0。
IGA算法步骤:
① 创建初始群体A1;
② 判断是否符合条件,符合则停止;
③ 对当前群体执行交叉、变异操作得到下一代;
④ 执行抗体、免疫操作,跳转到②。
在本文中使用免疫遗传算法来优化模糊神经网络和控制器的增益,如果将模糊神经控制器的增益固定为一个常数,那么随着工况的变化,控制效果就会变差,所以本文使用免疫遗传算法来优化控制器增益。系统控制结构图如下: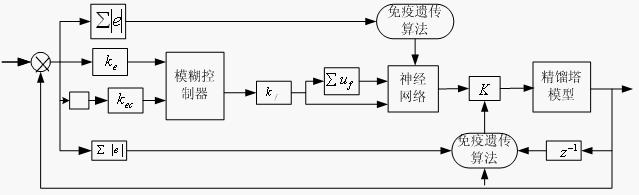
图3 整体控制方案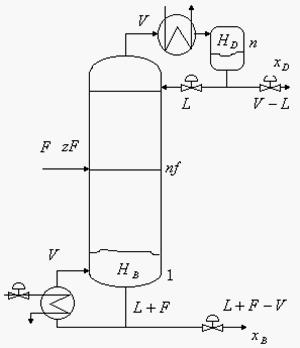
图4 精馏塔结构3 精馏塔简介
一个简单的精馏塔由塔板段、冷凝器和再沸器组成,图4-1是一个简单精馏塔原理图。精馏塔内有上下流动的物流,蒸汽在塔顶冷凝器中冷凝得到馏出液,部分作为回流液流回塔里,逐板下流,使各塔板保持一定的液位。
假设在塔的中部某个塔板进料,则进料塔板以下至塔底称为提馏段,进料塔板以上至塔顶称为精馏段。在塔的精馏段,料液中的蒸汽和提馏段来的汽相一起与塔顶回流液发生逆液接触和传质,液相中的易挥发组分向汽相传递,而汽相中的难挥发组分向液相传递。结果是,随着汽相的上升,其易挥发组分的含量越来越高,只要两相在塔内得到充分地接触和传质,塔顶就可得到相当纯净的易挥发物;而液相在下降的过程中,难挥发组分含量越来越高,塔底就得到纯净的难挥发物,从而达到分离的目的。
如果不考虑侧线抽出,则全塔有三个进出流量,分别是进料流量F,塔顶馏出量和塔底馏出量B。另外还有两个内部流量,分别是塔顶回流量L和塔底再沸器产生的蒸汽量V。假设混合物是一种二元物系,即只有两种挥发度不同的物质,我们以轻组分的含量来表示液体和气体的浓度。图4-1中几个流量和组分符号的含义是
L∶ 塔顶回流量;
V∶ 再沸器产生的蒸汽量;
XD∶塔顶馏出液轻组分含量;
XB∶塔底馏出液轻组分含量;
F∶ 进料流量;
ZF∶进料中轻组分含量;
qF∶进料中液体含量。
其中L、V是操作变量(即控制变量),被控变量是XD和XB,而F,ZF和qF是干扰变量。精馏塔控制的目的就是通过控制L、V这两个流量,在有F,ZF和qF干扰的情况下使XD和XB具有要求的调节和跟踪特性。
4 精馏塔模型
假设精馏塔具有n层理论塔板,塔板号从下往上数,即塔底再沸器是第1层塔板,塔顶冷凝器是第n层塔板,第nf层塔板进料。二元物系的相对挥发度是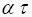 。一个精馏塔实例的参数值见表1。
。一个精馏塔实例的参数值见表1。
由恒相对挥发度假设,汽液平衡方程为
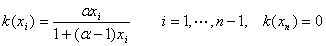 (9)
(9)
因为忽略气体滞留量,所以每层塔板的气体流量相同,都等于再沸器的气体流出量。
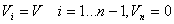 (10)
(10)
表1. 精馏塔特性数据
稳态时,每层塔板的滞液量都是0.5kmol。其他稳态数据如下表。
表2. 精馏塔稳态数据
图5是精馏塔普通塔板、进料塔板、冷凝器和再沸器的原理图。由前面的模型假设,根据物料平衡,可以对塔板、冷凝器和再沸器列写动态方程。
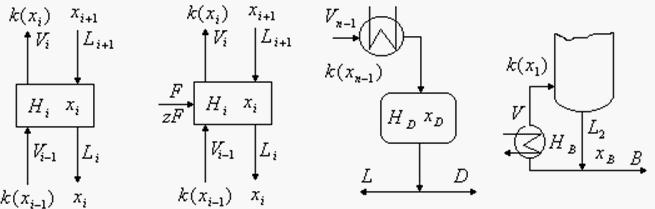
图5 普通塔板、进料塔板、冷凝器和再沸器原理图由精馏塔模型的假设,可得到如下的动态数学模型。
塔底再沸器∶
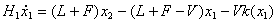 (11)
(11)
提馏段塔板∶
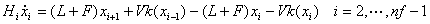 (12)
(12)
进料塔板∶
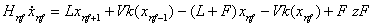 (13)
(13)
精馏段塔板∶
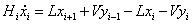
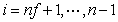 (14)
(14)
全冷凝器∶
 (15)
(15)
观察模型方程可以发现,精馏塔模型具有三对角结构,即一个塔板的状态只与相临塔板的状态直接关联。
5 仿真研究及结论
对模型进行仿真可以得到:
图6 模型仿真图由图可以看出精馏塔是一个非常缓慢的自衡系统,产生一个20个染色体的种群,W1,W2,b分别使用范围[-1,1],
 使用范围[0,4]来输入到优化的IGA-NN中。使用文中控制器进行仿真得到:
使用范围[0,4]来输入到优化的IGA-NN中。使用文中控制器进行仿真得到: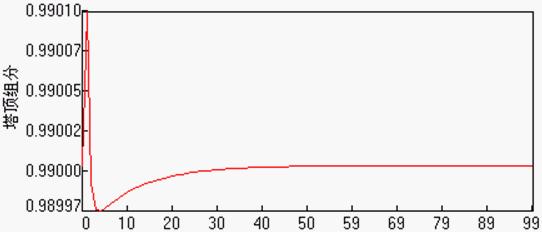
图7 控制塔顶组分图6 参考文献
作者信息:
[1] ZHOU Wei liang , HE Kun , CAO Xian bin, et al. Immune genetic algorithm for designing BP network[J]. Journal of Anhui University: Natural Science, 1999, 23 (1): 63-66.
[2] YANG Feng Shan, LI Ying Hong, LI Zheng Xi. Research on hybrid PID design and immolation[J]. Journal of North China University of Technology, 2003, 15 (3): 64-66.
[3] Licheng Jiao, Lei Wang. A Novel Genetic Algorithm Based on Immunity. IEEE Transactions on Systems, Man, and Cybernetics-part A: systems and humans. 2000, vol.30: 552-553
[4] J.S.Zhang, Z.B.Xu, and Y.Liang. The whole annealing genetic algorithms and their sufficient and necessary conditions of convergence[J]. Science in china. 1997, vol.27, no.2: 154-164
郭小青 (1)江西省吉安市第二中学343000;
晏琼 (2)江西省吉安市吉州区长塘中学343000;
晏琦 (3)艾默生过程控制有限公司





.jpg)




