控制网

    黄超（1983—）
男，河南信阳人，同济大学硕士研究生，研究方向为控制理论与控制工程。

摘 要：在将焊管切割为符合 API 标准的石油管的生产过程中，由于生产线中各设备及环境等因素的影响，使得生产出来的焊管质量存在许多不可预见的缺陷，这就意味着很难根据已知条件来建立优化模型，本文正是针对这一问题，在生产过程中采用遗传算法对焊管切割过程进行动态优化，提高钢管原材料的利用率，并用于国内的焊管生产线系统中。

关键词：焊管生产线；API 标准；遗传算法；优化切割

Abstract : Because of the effect of the devices of the production lines and environment during the produeing of API pipes, there are many unpredictable faults in the quality of the pipes. It is difficult to make the optimum mathematical model by means of the present condition. In this paper, genetic arithmetic programming is applied to the cutting operations in production lines . It provides capability to reduce cutting loss, thus to save material. This method has been used in domestic production lines.

Key words : pipe production line; API; Genetic arithmetic; optimization cutting

1 引言

    目前，国内大型焊管生产线已初具规模，下一步正朝着生产系统上位计算机对整条生产线的智能管理发展，而其中一个最主要的部分就是焊管的优化切割。国内焊管生产线中切割部分均是采用西门子SINUMERIC 840D为控制系统，在切割前上位计算机规划好切割钢管长度，切割时执行切割规划。

    目前国内大部分还在使用人工指定长度的切割，造成了钢材的大量浪费。结合焊管生产线的实际生产工艺条件，本文提出了用遗传算法思想的搜索来解决实际钢管切割中存在的复杂优化问题，阐述了其他传统优化方法的局限性，填补了国内该行业内解决本问题的空白。

2 焊管生产线工艺流程

    焊管生产线的原材料是钢带,再卷成钢卷，经过下述工艺流程的各种处理，最终生产出定长度钢管的生产系统。

    工艺流程如下：

    纵剪 → 开卷 → 矫平 → 剪切对焊 → 螺旋活套 → 铣边 → FFX成型 → 高频焊接 → 去内外毛刺 → 超声波探伤 → 焊缝热处理 → 空冷水冷 → 定径 → 矫直 → 打印标志 → 切断 → 出料

3 优化锯切

    3.1  影响锯切的因素

    3.1.1整线停机

    由于整线启动时，各工艺设备不能达到正常工作状态造成废管。实验表明停机一次会在生产线造成总长到14米的缺陷，因此避免整线停机为提高钢管率的一个重要目标。

    3.1.2缺陷

    焊管在成形过程中不可避免地存在缺陷，最重要的有整线停机缺陷，焊缝热处理缺陷，超声波探伤所得缺陷等。

    缺陷中还存在着缺陷程度等级，分为严重缺陷和一般缺陷。

    严重缺陷：存在开口的焊管，焊管的开口段极易损坏切割飞锯的锯片,造成很大的损失。

    一般缺陷：无开口但不符合产品合格质量的焊管段。

    3.1.3生产限制

    生产限制即用户合格品要求的长度，本文所提及的即为美国石油钢管API标准切割长度要求。API标准中并不是指定一个定长的焊管，而是一个合格范围，满足该范围即为合格品。

    3.1.4物理限制

    物理限制是指生产系统的能力范围,即整个焊管生产线能生产出来的焊管的最小管长和最大管长，由于输出辊道出料机构的机械设计，生产线不可能生产出任何长度的焊管。

    3.2  优化锯切的目的

    在生产限制和物理限制的范围内，对缺陷检测装置结束处到焊管头部的整段焊管进行规划，以满足能出料、适合下刀的条件下提高焊管上无缺陷段的利用率。

    3.3优化锯切的原则

    3.3.1出产的焊管要在物理限制的范围内，能出料以保持生产线生产的连续性。

    3.3.2不能在严重缺陷上下刀，以保证不损坏锯片和生产线的连续性。

    3.3.3如果切下的焊管上带有缺陷段，但除去缺陷点后的好管段在生产限制范围内，同样认为为合格管。
　　
4 优化锯切的方法

    4.1  优化方法的提出

    在本问题中，很难由传统的优化方法找出一个令人满意的方案，因为在规划前，根本无法确定目标函数，在未做规划的情况下根据锯切的原则无法确定哪段为合格管，哪段为废管。只能通过已经规划过的方案，分析该方案，建立起对该方案的评价函数，来找出对该方案的满意度，从而指导搜索向满意度更高的方案进行，最后选择择最高满意度的方案为最优化方案。遗传算法正是这类算法，通过评价导向搜索，从而找到全局的最优。

    4.2  优化锯切的算法实现

    4.2.1遗传模型建立

    建立以切割的开始点为原点的一维坐标系             。

    直观地选取优化的一个管长作为染色体的一个解，而优化Pnum根则构成了一个染色体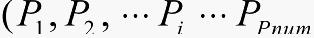)，而找出评价最好的染色体即对应找出了整线的优化切割管长的序列。
    约束条件：

   

   

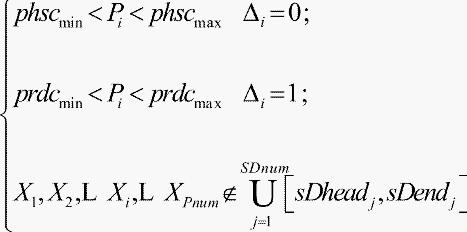
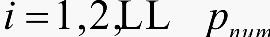
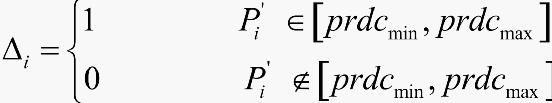
    其中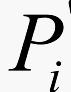为P_i的最长无缺陷长度,[phsc_min,pshc_max]为生产线焊管切割的物理管长限制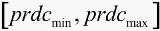，为生出合格品的生产限制规格，X_i即为第P_i根管尾的切割点在坐标系Axis上的坐标。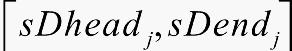为整线上第j个严重缺陷转化为坐标系上的区间集合。

    选取评价函数为算法实现中一个最重要的部分，它需要能反映出优化序列的好坏以及好坏的程度以指导遗传的搜索方向。评价的方法为：不做拒绝，凡是染色体的解满足物理限制则认为是可行解，然后通过对利用率加上惩罚函数来评价分配方案。

    评价函数定义为： 对于给定染色体)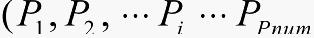 

   

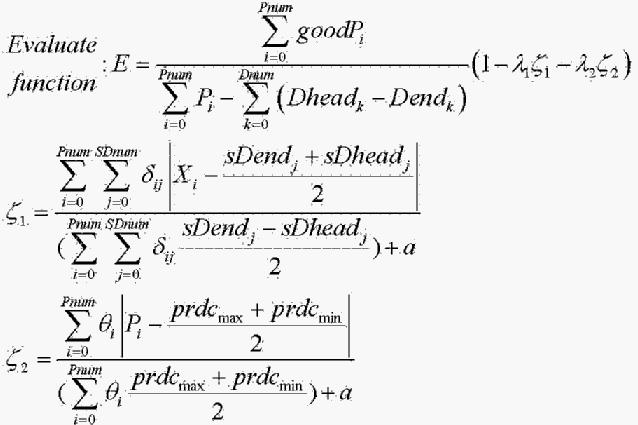
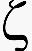    ₁为切割点落在严重缺陷上的惩罚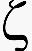，₂为不含缺陷管的惩罚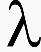，₁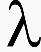，₂分别为各自权重。

   

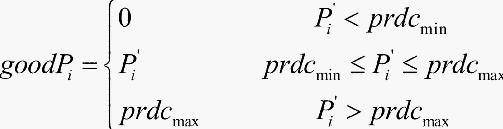
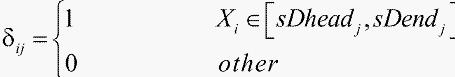
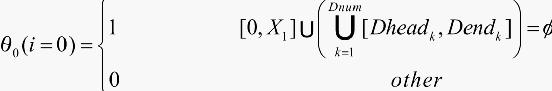
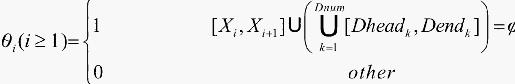
    [Dhead_k,Dhend_k]为整线上第k个缺陷转化为坐标系Axis上的区间集合,a为一个极小的正数，以限制分母不分零。

    4.2.2遗传求解过程

    4.2.2.1 初始化染色体

    随机产生PopSize个满足P_i在[phsc_min,phsc_max]内的染色体。 

    4.2.2.2 交叉
对于双亲V₁和V₂交叉运算产生的后代V_^'1和V_^'2如下：
      
                    
  
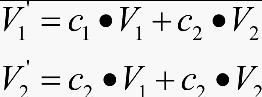
    其中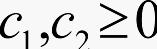，且C₁+C₂=1交叉时有一个重要的参数交差率P_c，它是种群中参加变异的染色体的概率。

    4.2.2.3变异

    通过变异律P_m，从种群里随机选择染色体V₀进行变异。利用选中的染色体和一个大数M₀来寻找变异结果，具体为，随机选取一个方向d。令M=M₀若V₀+M?d可行，取其为新染色体，否则令M为(0,M)的随机数，直到V₀+M?d可行，产生出新的变异染色体。
    4.2.2.4选择

    采用确定型选择，就是删去双亲和后代中所有重复的染色体，将余下的染色体按降序排列，然后选择前PopSize个染色体作为新的种群。

    4.2.2.5算法停止条件

    当优化切割总管长上好段的利用率达到一个数值，或都已经到达设定的最大数时停止计算。

    4.2.3算法流程图（如图1所示）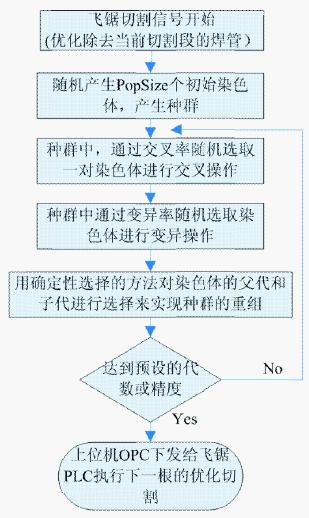

图1   算法流程图

5  优化锯切仿真结果研究

    自行编制了模拟程序，开始时让程序随机的产生一系列的各种严重程度的缺陷，再结合普通生产中所需要的实际要求，优化参数为[pshc_min,pshc_max]为[6,18],[prdc_min,prdc_max]为[8,12],Pnum=8, PopSize=400, 大数M₀=10000, 运算次数为100代，交差率Pc=0.8, 变异率P_m=0.1,加权值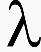₁=0.3,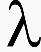₂=0.6运行模拟后数据见表1。

     表一：

其它作者：

    朱劲，（1958-），男，湖南长沙人，副教授，同济大学硕士生导师，研究方向为控制理论与控制工程，机器人控制与智能控制。
　　
参考文献

    [1] (日)玄光男, 程润伟.遗传算法与工程设计. 科学出版社， 2000. 

    [2] 张文修, 梁怡编. 遗传算法的数学基础. 西安交通大学出版社， 2000.

    [3] (美)Z. 米凯利维茨.演化程序:遗传算法和数据编码的结合.科学出版社， 2000.

    [4] 王小平, 曹立明. 遗传算法:理论、应用与软件实现. 西安交通大学出版社， 2002.

    [5]YU Hua,SUI Jie,JIAO Jianbin,et al.Mould manufacture optimum in different place based on GA[J].Computer Integrated Manufacturing Systems,2001,7(1):51-54 (in Chinese).[于华,隋杰,焦建彬,等.基于遗传算法的模具异地制造得优化调度[J].计算机集成制造系统,2001,7(1):51-54.]