控制网

    李宗杰（1983－）
男，浙江人，（华北计算机系统工程研究所，北京  100083）华北计算机系统工程研究所硕士研究在读生，研究方向为计算机工业过程控制。

摘要：本论文首先描述了一种数据恢复功能的总体设计思想；在此基础上，根据树型数据结构的特点，具体化总体设计思想，设计出一套高效数据恢复功能的实现方案，达到时间和空间上的优化；最后，以接近C++的伪代码方式，描述了该方案实现的部分算法。

关键词：树型结构；数据恢复；撤销；重复

Abstract: This paper describes a total strategy on recovery of data. According to the characteristic of tree structure, the paper shows a concrete shape of total strategy just mentioned to realize the recovery of tree structure effectively. At last, the algorithm implementation is given by the C++ pseudo-code.

Key words:  Tree Structure；Data Recovery；Undo；Redo

1 引言

    很多的软件离不开数据的操作，包括数据的修改、删除和增加，而在操作的时候，用户存在误操作的可能，尤其是一些编辑软件，例如微软的word、excel等。在这种情况下，如果软件提供数据恢复的功能，用户将可以十分方便的通过此功能使数据回到历史的某个状态。

    另一方面，树型结构是一种应用十分广泛的数据结构，比如组织结构，物料清单，资料档案管理，资产管理等等都是以树型结构为基础。在现实生活中，有许多事物可以抽象为树状结构。这种结构可以简化对某些事物的理解，使概念清晰[1]。而且，树作为一种常见的数据结构，已经有了一套成熟的研究成果。因此，有很多项目采用树型结构来抽象具体的事物，实现软件的开发。

    为此，对树型结构数据恢复功能的探讨是很有意义的。

    下文首先描述了一个可行的比较通用的数据恢复设计思想，在此基础上，分析树型数据结构的特点，设计出一套针对树型数据结构的高效数据恢复方案。

2 总体设计思想

    实现数据恢复的前提是记录各个时刻的历史信息，即各个时刻的数据；然后，在必要的时候响应“撤销”、“重复”的命令，实现历史的无损复现。

    从“撤销、重复”操作的角度，可以把不同时间点的内存数据信息划分为三个状态：过去式、当前、将来式。

    在每一个时间点上都有其对应的数据信息。在响应用户“撤销”或“重复”操作后，当前内存数据就需要恢复到特定时刻的内存数据。要实现这样的功能，显然，在每一个时间点上，需要记录反映此时内存数据信息的相关信息（简称为关键信息）。

    “时间点”可以根据每个软件的具体情况，在设计的时候予以明确，一般地可以定义在增加数据，删除数据，修改数据的时刻。下文为了便于说明，单独使用修改的时候，“修改”的涵义包含了“增加”和“删除”。

    以当前状态为分界点，在当前状态以前的各个时刻的状态称为过去式状态，在当前状态以后的各个时刻的状态称为将来式状态。在实现上，过去式和将来式的状态都采用“栈”的结构来存储。

    图1描述了在各状态的转换情况。

图1   状态变化示意图

    历史记录要求有延续性，不允许在历史中间插入一个新的状态，因为如果在中间插入一个新的状态，那么整个历史记录就是一个乱序的状态集合，而不是一个连续的状态集合。在修改后即有了新的状态，而这个原来的状态是在历史中间的某个时间点上，那么新的状态应该怎么记录呢？在这种情况下，只有删除原来状态后面的所有历史记录，形成一个新的历史记录表。

3 树型结构的特点

    树是以分支关系定义的层次结构。树是n个结点的有限集，在一棵非空树中有且仅有一个特定的称为根的结点；其余结点可分为若干个互不相交的有限集，其中每一个集合的本身又是一棵树，并且称为根的子树[1]。例如，图2的内容是一棵有15个结点的树，其中A是根，其余结点分成四个互不相交的子集：T1 = {a}，T2 = {B，c，D，f，g，h}，T3 = {C，E，i，j，k}，T4 = {b}；T1、T2、T3和T4都是根A的子树，且本身也是一棵树。例如T2，其根为B（下文中称呼为分支的根结点），其余结点分为三个互不相交的子集：T21 = {c}，T22 = {D，f，g，h}，T23 = {d}。T21、T22、T23都是B的子树。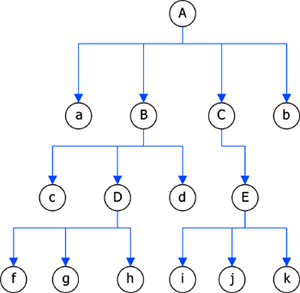

图2   树的示例图

    树的结点包含一个数据元素及若干指向其子树的分支。结点拥有的子树称为结点的度。例如图2中，A的度为4，a的度为0。度为0的结点称为叶子。结点子树的根称为该结点的孩子（又称为子结点），相应地，该节点成为孩子的双亲（又称为父结点）。子结点有唯一一个父结点，父结点可以有多个子结点。

4 树型结构的数据恢复设计

    在“总体设计思想”一节中，描述了整体的设计思路。其中，关键点在于确定每一个“时间点”需要记录的是哪些信息。
最直接的做法是把当前时刻的所有数据信息都记录下来，这样回到任何时刻的状态都不会有问题，而且，对于任何的数据结构，都是适用的。但是，这种方式存在着明显的缺点。首先，由于历史记录的数目大，占用了大量的内存空间；其次，每次需要恢复大量的数据，这些附加的操作降低了程序运行的效率。

    树是以分支关系定义的层次结构，根据树型结构的这一特点，可以把“关键信息”选择为单个“结点”。

    4.1 方案的可行性

    “撤销”、“重复”操作涉及的状态是相邻时刻的状态，因此它们之间的数据有很多是一样的，有变化的只是数据信息中的一部分，这些变化体现在树型结构上就是某一棵子树的变化，本子树的概念大则包括整棵树，小则指单个叶子结点。子树的根结点就是需要记录的关键信息。

    图3左边是上一状态的树，右边是下一状态的树，子树C下的成员在当前状态下被删除了。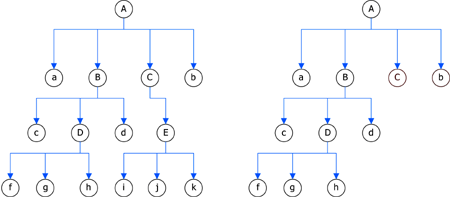

图3   相邻状态举例

    图3中，变化的子树为T = {C，E，i，j，k}，其中，E、i、j、k结点在当前状态下被删除了。在此情况下，过去式栈的栈顶成员（当前状态上一状态的关键信息）就是结点C。而E、i、j、k结点并没有被记录下来，这样如果用户想回到图中左边的数据状态，怎样复现E、i、j、k采用“虚拟删除”的方案。

    在删除数据元素的时候，不是真正的删除操作，如上图中的元素E从C中删除，那么需要切断C与E的父、子结点的关系，形成两棵独立的树；同时，如果内存数据元素是可以被用户直接操作的，需要修改元素的属性，屏蔽这些元素达到删除的效果。因此，在某一历史状态下的内存数据可以分为：当前可用的数据信息和当前不可用的数据信息（虚拟删除的信息）。

    在数据保存的时候，只需要保存当前可用的数据信息，不需要保存已经标识为删除的元素和历史栈中的备份元素；而且保存操作之后，不需要再维持数据恢复功能，因此，在保存之前可以把历史栈和带删除标记的元素彻底删除。

    4.2 关键结点的查找

    在修改操作发生的时候，需要记录新的关键结点。新的关键结点不是被操作的结点，而是子树的根结点。

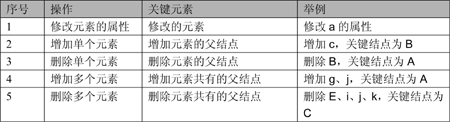
    下面从修改单个元素、多个元素不同的角度去分析关键结点的查找。前提：“修改元素的属性”操作只适用于单个元素。

表1   各种操作的关键元素

    4.3 恢复过程

    恢复过程可以分为撤销和重复两种情况。它们共同的操作除了进、出栈外，还包括根据出栈的元素找到当前状态下与之对应的元素，完成替换操作。

    下面以接近C++的伪码方式，描述本方案实现的主要算法。

    元素（结点）：

Class CElement
{
　　Attribute：
　　 Integer  ID；  //元素的ID号，标识元素
Integer  parentID； //父结点的ID
Integer  index；  //在父结点的成员列表中的索引
Integer deepInTree； //元素在树中所处的层次
CList  childIDList； //子结点成员列表
Bool  deleteFlag； //删除标志
 Method：
  GetParent()；   //得到父结点
  GetChild(Integer index)； //得到索引为index的子结点
  CopyElement()；  //备份该元素
  ShutElement()；  //屏蔽所有子元素，屏蔽的子元素需要设置deleteFlag
  ActiveElement()； //激活所有子元素，清除子元素的deleteFlag
  DeleteElement()； //虚拟删除本元素，把子成员插入到父结点成员表中
}

    内存元素表：CMap  ElementMap； //以元素ID为关键字，元素指针为值

    过去式栈、将来式栈：pastStack、futureStack  //存放备份的元素的指针

    约束条件：树根结点是不可操作的

    算法1：寻找关键结点（本算法适合操作两个元素；如果超过两个元素，可以由多次两个元素操作的叠加来完成），完成后返回关键结点的ID号。

Integer SearchBranchRoot(Integer IDOne， Integer IDTwo)
{
　　ElementMap.GetAt(IDOne，pElementOne)；
　　ElementMap.GetAt(IDTwo，pElementTwo)；
　　IF pElementOne->deepInTree = = pElementTwo->deepInTree
       IF pElementOne->parentID = = pElementTwo->ParentID
　　   RETURN pElementOne->parentID；
       ELSE
　　   RETURN SearchBranch(pElementOne->parentID，pElementTwo->parentID)；
　　ELSE
       IF pElementOne->deepInTree > pElementTwo->deepInTree
　　    RETURN SearchBranch(pElementOne->parentID，pElementTwo)；
       ELSE
　　    RETURN SearchBranch(pElementOne，pElementTwo->parentID)；
}
　　算法2：撤销操作
　　Void Undo()
　　{
　　 pElement = pastStack.Pop()；
　　 ElementMap.GetAt(pElement.ID，pOriginal)；//找到备份元素的原型
　　 pOriginal->ShutElement()；
　　 pElement->ActiveElement()；//本条语句与上条语句的顺序不可颠倒
　　 ElementMap.SetAt(pElement.ID，pElement)?；//取代
　　 futureStack.Push(pOriginal)?；
　　}
　　算法3：重复操作
　　Void Redo()
　　{
　　 pElement = futureStack.Pop()；
　　 ElementMap.GetAt(pElement.ID，pOriginal)；//找到备份元素的原型
　　 pOriginal->ShutElement()；
　　 pElement->ActiveElement()；
　　 ElementMap.SetAt(pElement.ID，pElement)?；//取代
　　 pastStack.Push(pOriginal)?；
　　}

5 结语

    本文介绍了一种树型结构数据恢复的方案，该方案在时间和空间上都体现了高效性，并成功应用在实际的软件开发项目中。
　　
参考文献：

    [1] 严蔚敏,吴伟民等.数据结构[M].北京：清华大学出版社，2002.

    [2] Donald E. Knuth，计算机程序设计艺术（影印版）[M].北京:清华大学出版社，2002.

    [3] 潘金贵（编译）.现代计算机常用数据结构和算法[M].南京：南京大学出版社，1992.