当前位置:首页»企业
- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 具有圆盘极点约束的不确定切换系统的鲁棒控制 技术领域 工业安全 行业 简介 本文研究了一类具有圆盘极点约束的不确定线性切换系统的鲁棒镇定问题.对此类系统设计了状态反馈控制器,使得闭环系统的所有极点均位于一个给定的圆盘中,并得到了一个基于LMI的充分条件.通过求解线性矩阵不等式,可以构造一个具有较小反馈增益参数的状态反馈控制器.最后的仿真算例证明了本文结果的有效性。 内容 
程娟 (1984-)
女,湖北黄冈人,硕士研究生,研究方向为切换系统、时滞依赖、极点配置、鲁棒控制。
摘要:本文研究了一类具有圆盘极点约束的不确定线性切换系统的鲁棒镇定问题.对此类系统设计了状态反馈控制器,使得闭环系统的所有极点均位于一个给定的圆盘中,并得到了一个基于LMI的充分条件.通过求解线性矩阵不等式,可以构造一个具有较小反馈增益参数的状态反馈控制器.最后的仿真算例证明了本文结果的有效性。
关键词:切换系统;鲁棒控制;极点配置;状态反馈
Abstract: The robust stabilization for uncertain linear switched systems with disk polo
constraints is studied in this paper,. State feedback controller is designed so that the
poles of the closedloop system can be assigned in a prespecified disk. A sufficient
condition based on LMI is therefore obtained. The problem of designing the controllers with
smaller gain parameters is solved based on LMI conditions. The simulation shows the
validity of the results.
Key words: switched systems; robust control; pole assignment; state feedback
1 引言
切换系统由于其广泛的应用背景得到了极大的关注,主要集中在切换系统的稳定性和鲁棒镇定问题的研究上,对闭环系统设计反馈控制器的一个基本要求就是将极点配置在指定的位置上,从而保证闭环系统的动态性和稳定性。近年来对具有极点约束的不确定系统的研究已经有很多结果成果[1-3],文献[5]将一类不确定闭环系统的极点配置在一个给定圆盘中,并设计状态反馈控制器,文献[6]讨论了一类具有闭环极点约束的线性离散系统的输出反馈控制问题,文献[7]利用状态反馈的方法得到了极点在椭圆形区域中的不确定线性系统的充分条件。这几篇文章讨论的都是一般系统,未涉及到切换系统。
本文研究了一类不确定切换系统,将其闭环系统的极点配置在一个给定的圆盘中,并设计了无记忆状态反馈控制器,最后采用基于LMI的处理方法得到了状态反馈控制器存在的条件和反馈增益参数.
2 问题描述
考虑如下的一类不确定切换系统
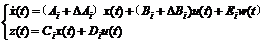 (1)
(1)

其中 ,
,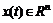 是系统的状态向量,
是系统的状态向量,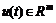 是系统的控制输入,
是系统的控制输入,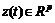 是系统的控制输出,
是系统的控制输出,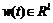 是外部扰动,
是外部扰动,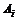 ,
, ,
,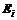 ,
,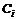 ,
, 是已知的具有适当维数的实常数矩阵,
是已知的具有适当维数的实常数矩阵,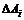 ,
,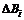 分别是状态向量和控制输入的不确定项,且满足下面的形式
分别是状态向量和控制输入的不确定项,且满足下面的形式
 (2)
(2)
其中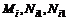 是具有适当维数的实常数矩阵,
是具有适当维数的实常数矩阵,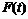 是满足
是满足 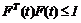 的未知矩阵,
的未知矩阵,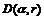 表示复平面上单位圆内中心在
表示复平面上单位圆内中心在 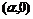 ,半径为
,半径为 的圆盘,其中
的圆盘,其中 和
和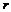 满足
满足 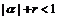 [8]。
[8]。
下面首先研究系统(1)的标称系统
 (3)
(3)
本文的目的是设计一个无记忆状态反馈控制器
 (4)
(4)
使得对所有允许的扰动,闭环系统
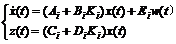 (5)
(5)
具有以下性质:
i) 所有闭环极点均位于预先给定的中心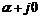 ,半径为
,半径为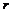 ,且满足
,且满足 的圆盘
的圆盘 中;
中;
ii) 从外部扰动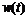 到被控输出的传递函数
到被控输出的传递函数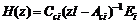 ,满足
,满足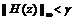 ,其中
,其中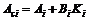 。
。
这样的一个问题就称为是系统(3)的鲁棒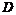 镇定问题,控制器(4)称为系统(5)的一个
镇定问题,控制器(4)称为系统(5)的一个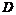 稳定
稳定 控制器。
控制器。
引理1给定矩阵 ,以及适当维数的矩阵
,以及适当维数的矩阵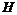 ,
,  则
则 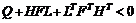 。对任意满足
。对任意满足 的
的 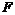 成立的充要条件是存在
成立的充要条件是存在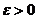 ,使得
,使得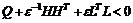 。
。
引理 2[4] 对给定单位圆内的圆盘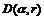 和正常数
和正常数 ,如果存在一个对称正定矩阵
,如果存在一个对称正定矩阵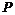 ,使得
,使得
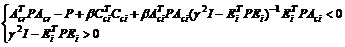 (6)
(6)
其中 ,
,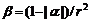 ,则系统(5)具有性质i)和ii)。
,则系统(5)具有性质i)和ii)。
3 主要结论
对系统(1)的标称系统(3)有如下的结论
定理1对给定单位圆内的圆盘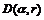 和正常数
和正常数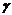 ,如果以下不等式成立
,如果以下不等式成立
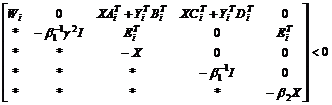 (7)
(7)
(*表示关于对角线的对称矩阵)当(7)式存在解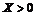 和
和 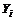 时,
时,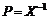 ,
,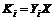 ,则系统(5)存在具有
,则系统(5)存在具有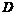 稳定
稳定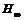 控制器(4)。其中
控制器(4)。其中
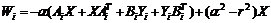
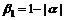 ,
,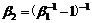
证明:对不等式(6)中的第一个不等式代入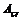 和
和 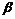 的表达式,经整理并利用矩阵的Schur补性质可得到如下等价不等式
的表达式,经整理并利用矩阵的Schur补性质可得到如下等价不等式
 (8)
(8)
其中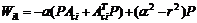 ,
,
代入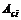 和
和 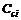 的表达式,可知不等式(8)是非线性的,为了将非线性不等式(8)转换成线性不等式,于是对不等式(8)左乘和右乘矩阵
的表达式,可知不等式(8)是非线性的,为了将非线性不等式(8)转换成线性不等式,于是对不等式(8)左乘和右乘矩阵 ,并令
,并令 , 即可得到不等式(8)等价于不等式(7),于是定理1得证。
, 即可得到不等式(8)等价于不等式(7),于是定理1得证。
下面考虑不确定线性切换系统(1),同理,对系统(1)设计一个无记忆状态反馈观测器
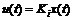 (9)
(9)
则得到的闭环系统为
 (10)
(10)
于是,对系统(10)我们有如下的结论
定理 2对给定单位圆内的圆盘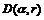 和正常数
和正常数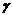 和
和 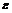 ,如果以下不等式成立
,如果以下不等式成立
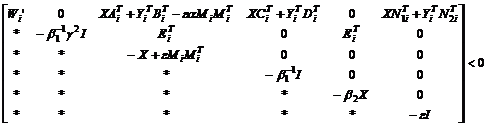 (11)
(11)
当(11)式存在解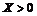 和
和 时,
时,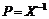 ,
,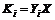 ,则系统(1)存在具有
,则系统(1)存在具有 稳定
稳定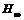 控制器(10)。其中
控制器(10)。其中
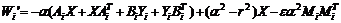 ,
,
 ,
,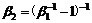 。
。
证明:对定理2的证明,只需将定理1中的 用
用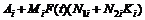 代替,并运用引理1,结合矩阵的Schur补性质,即可得到结论,在此略去。
代替,并运用引理1,结合矩阵的Schur补性质,即可得到结论,在此略去。
4 数值算例
下面给出一个简单的系统(1)的标称系统的数值算例。
对于系统(3)
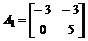 ;
; ;
;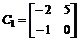 ;
;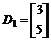 ;
;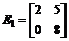 ;
;
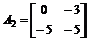 ;
;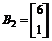 ;
;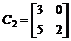 ;
;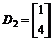 ;
;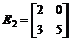 ;
;
图1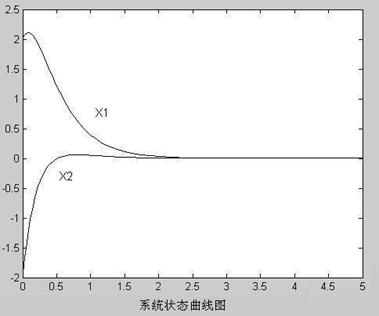
取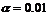 ,
,  ,
,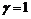 ,根据定理1利用MATLAB求得
,根据定理1利用MATLAB求得
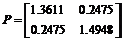 ;
;
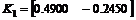 ;
;
 ;
;
该系统在初始状态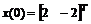 和切换规则为1秒切换一次,应用定理1,可以得到把各子系统极点配置在
和切换规则为1秒切换一次,应用定理1,可以得到把各子系统极点配置在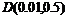 内且渐近稳定的结果,系统状态如图1所示。
内且渐近稳定的结果,系统状态如图1所示。
5 结论
本文研究了一类不确定切换系统具有圆盘极点约束的鲁棒控制问题,设计了状态反馈控制器,使得闭环系统的极点都配置在制定的圆盘区域内,得到了基于LMI的状态反馈存在的充分条件,并通过MATLAB求解出了反馈增益参数,最后给出了一个具有两个子系统的切换系统的仿真数例,其结果证明了本文结论的有效性。
参考文献
[1] Wassim M. Haddad, Dennis S. Bernstein. Controller design with regional pole constraints
[J]. IEEE Trans on Automatic Control. 1996,41(3): 358-366.
[2] Mahmoud Chilali, Pascal Gahinet. design with pole placement constraints: An LMI
Approach [J]. IEEE Trans on Automatic Control.1996,41(3): 358-366.
[3] Byung Soo Kim, Hyung Seok Han, Jang Gyu Lee. Pole placement of uncertain discrete
systems in the smallest disk by state feedback[C]. Proceedings of the 35th Conference on Decision and Control. 1996,4558-4563.
[4] Xu ShengYuan, Yang ChengWu, Zhou ShaoSheng. Robust control for uncertain discrete-time systems with circular pole constraints [J]. Systems &Control Letters. 2000,39(1):13-18.
[5] 俞力,陈国定,杨马英. 不确定系统具有圆盘区域极点约束的鲁棒控制 [J]. 自动化学报. 2000,26(1):116-120.
[6] 俞力,杨海清. 线性离散系统具有闭环极点约束的输出反馈控制[J]. 控制理论与应用. 2003,20(5): 773-775.
[7] 王天波,张学山,方涛. 具有区域极点约束的不确定系统的鲁棒控制[J]. 上海工程技术大学学报[J]. 2007,21(1): 69-72.
[8] 俞力. 鲁棒控制: 线性矩阵不等式处理方法[M]. 北京: 清华大学出版社,2002.





.jpg)




