- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 轴承数据的Matlab高阶谱分析 技术领域 运动控制 行业 简介 使用matlab高阶谱工具箱(HOSA)函数对轴承数据进行分析,介绍了若干在仿真中用到的HOSA函数及其数学基础。并验证,由于轴承振动信号的非高斯、非线性特性,低阶统计量不能分辨的振动特征,能够通过高阶统计量及其matlab工具进行分析 内容 1 引言
轴承是工业生产中使用最广泛的机械部件,也是最易损伤的零件之一。有故障的轴承不仅会直接影响设备的基本性能,而且有可能造成重大生产事故。我国是轴承制造大国,目前,轴承产量居世界首位,产值第三,仅次于美国和日本。我国也是轴承使用大国,每年进口大量高档轴承用于机械设备制造。因此,能对有故障轴承进行识别的技术具有重要的实际意义和应用前景。
轴承诊断技术众多。其中,振动检测法是通过分析轴承工作时的振动信号对其进行故障识别的方法。由于测试方便,分析直观,在故障检测中有着广泛的应用。在并不需要很高精度的情况下,振动信号的低阶统计量,对质量问题明显的轴承有一定的鉴别作用。低阶统计量能够确定零均值平稳高斯过程的统计特性。但是,现在很多精密轴承通常故障微小,很多信息表现为非高斯性,非线性,非最小相位等特点,低阶统计量无法进行识别。高阶统计量是在低阶统计理论基础上发展起来的,克服了低阶统计量由于缺少相位信息而无法直接处理非最小相位系统的固有缺陷,能对非高斯,非线性,非最小相位系统进行分析。也就是说,用低阶统计量方法不能圆满解决的问题,理论上都可以用高阶统计量进行处理【1】。
高阶谱工具箱是专用的Matlab信号处理工具箱,功能强大。包含了传统方法的高阶谱估计,参数方法的高阶谱估计,二次相位耦合,谐波恢复,时间延迟估计,自适应线性预测等多种分析方法。本文采用传统方法的高阶谱函数,介绍了高阶谱工具箱在轴承故障分析中的应用。
2 高阶累计量和高阶谱
最常用的高阶统计量是高阶累积量和高阶谱。平稳过程的一阶累计量定义为均值:
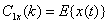 (1)
(1)
均值平移不会改变高阶累积量,因此,可假设均值为零。如果均值为非零,先减去均值,再处理随机过程的高阶累积量。
零均值平稳过程的累积量定义如下【2】:
二阶累积量: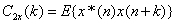 (2)
(2)
三阶累积量: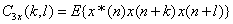 (3)
(3)
.第k阶谱定义为对应累积量序列的傅里叶变换:
功率谱: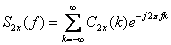 (4)
(4)
双谱: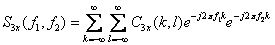 (5)
(5)
互双谱: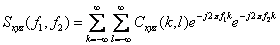 (6)
(6)
双谱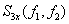 是互双谱取x=y=z时的特例。
是互双谱取x=y=z时的特例。
互相干: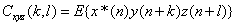 (7)
(7)
互双相干定义为: (8)
(8)
当x=y=z时,便是自双相干。
3 轴承数据的高阶统计量估计
Matlab的HOSA(High-Order Spectrum Analysis Toolbox)是专用的高阶谱信号处理工具箱,包含传统方法,参数 方法,二次相位耦合,二阶Volterrra系统,谐波恢复,时间延迟估计(TDE),阵列处理,自适应线性预测,脉冲响应,时频估计等类别的函数。
下面使用几个工具箱函数来对轴承振动数据进行分析和比较。
高阶谱的基本工具是三阶累积量对应的双谱分析,在工具箱中,有间接双谱估计函数bispeci,直接双谱估计函数bispecd,直接互双谱估计函数bispecdx。下面对bispecd作简单的函数说明,并观测bispeci与bispecd对合格与故障数据的估计结果。
function [Bspec,waxis] = bispecd (y, nfft, wind, nsamp, overlap)
功能:基于FFT变换的直接方法双谱估计。
参数说明:
y: 信号序列,矩阵或向量;
nfft: FFT变换计算长度;
wind: 指定窗函数,起频域平滑的作用;
nsamp: 指定每段数据估计时的样本数目,默认是y的行数量;
overlap: 指定相邻数据重叠百分比,取值范围[0, 99],默认值为0;
Bspec: 估计双谱返回矩阵,nfft×nfft矩阵;
Waxis: 与bspec矩阵相关的频率,第i行(列)bspec与Waxis(i)相关。
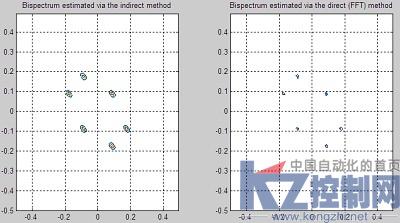
图1 间接与直接双谱估计合格轴承振动数据
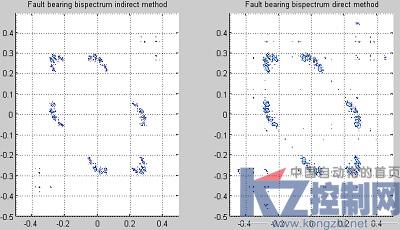
图2 间接与直接双谱估计故障轴承振动数据
可以看到,直接双谱与间接双谱估计效果差不多,都能够非常清晰的地分辨合格与故障轴承。图1显示双谱估计对合格轴承振动的特征频率有很好的提取作用。对比图1,图2的显示结果表明,由于故障振动表现为周期性的冲击振动和幅值调制现象[3],故障特征频率经过双谱估计,特征信号分布在一个相对小的范围内,表现出相当强的特性。特征信号的图形表明,通过智能学习算法对Bspec和waxis变量的分析,应该可以很容易分辨合格与故障轴承,并且分析轴承的故障类型。
在HOSA工具箱中, bicoher用来估计自双相干, bicoherx用来估计互双相干。下面的图形将显示bicoher函数估计合格与故障轴承的情况
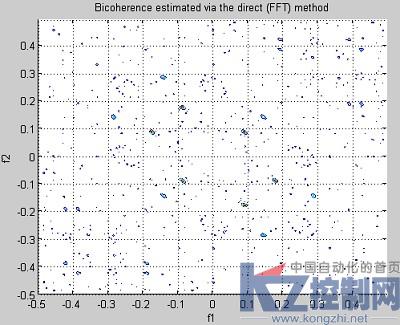
图3 自双相干估计合格轴承振动数据
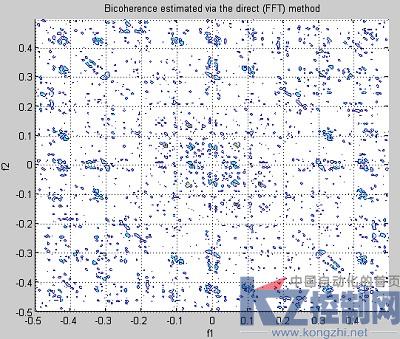
图4 自双相干估计故障轴承振动数据
根据公式(8),自双相干是基于功率谱和双谱的一个估计。而功率谱是二阶累积量的傅里叶变换,从图3和图4看到,自双相干估计难以对合格和故障轴承振动信号进行有效的特征提取,图形中显示了很多干扰信号。仿真表明,二阶统计量不能对轴承的合格与故障信号进行有效的特征提取。
4 结论
自相干的估计结果表明:轴承振动信号具有的非高斯,非线性等特性不能用二阶以下的统计量进行表征。双谱估计的结果表明:用二阶不能解决的问题,三阶谱能有效地提取信号特性。本文验证了高阶统计量理论及HOSA工具箱对轴承振动信号的应用性,体现了其在轴承检测过程中的应用前景。
参考文献:
[1] 张贤达, 保铮.非平稳信号分析与处理[M]. 国防工业出版社, 1998.
[2] A.Swami, Jerry M. Mendel, C.L. Nikias High-Order Spectral Analysis Toolbox For Use with Matlab[M]. 2004.
[3] 姜鸣.循环统计量理路及其在滚动轴承故障中的应用研究[D]. 上海:上海交通大学, 2002.
[4] 柳桂国,柳贺,黄道.经验正交函数分析在轴承故障诊断中的应用[J]. 华东理工大学学报, 2008, Vol.34 No.2:261-266
乐斌(1978-)
男,宁波人,硕士研究生,高级工程师,主要从事模式识别、智能系统方面的研究,现就职于浙江工商职业技术学院。
摘自《自动化博览》2011年第二期





.jpg)




