- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 精密仪器的运动控制模型与实现 技术领域 运动控制 行业 简介 本文对精密仪器中的微型无刷永磁直流电机进行高精度、低成本的控制问题进行了分析,在对电机的数学模型的分析基础上,采用模型参数匹配设计方法,计算出基于PID控制参数,并给出其电路实现 内容 1、问题的提出
精密仪器的运动单元一般均采用微型无刷永磁直流电机,电机尺寸以及安装空间很小,对电机的控制精度要求较高,一般要求达到0.5%~0.1%,另外在某些应用中对成本控制的要求较高。
通常直流电机的控制多采用速度/力矩负反馈闭环控制,可以做到高精度控制。但需要给电机安装编码器、力矩传感器等器件进行控制参数的测量,并设置控制电路进行控制[1],这种方案因为体积/成本原因对精密仪器电机的控制是不可行的。
近些年来,常采用电子稳速电路对小型直流电机进行控制,图1是一种典型的电子稳速电路。其中G1是调速管,G2是比较放大管,W是速度微调电阻。但它只是单纯应用电机的反相电动势负反馈原理进行控制,其控制精度差,一般大于0.5%,并且超调大,过渡时间长,不能满足精密仪器的控制精度要求。
.gif)
图1 典型的电子稳速电路
2、电机数学模型分析
微型无刷永磁直流电机的等效电路如图2所示。
.gif)
图2 无刷永磁直流电机等效电路
其中:U为输入电压,ω为输出角频率,R为等效内阻,L为等效感抗,I为电机电流,E为电枢反应的反电势,ML为负载扰动力矩。
由电路原理可知:.gif) (1)
(1)
电枢反应的反电势E与ω的关系是:.gif) (2)
(2)
其中:ke为电势系数,由电机结构参数决定。
由刚体旋转定律可写出电机轴上的机械运动方程:.gif) (3)
(3)
其中:M是电机的输出转矩,并且存在.gif) ,km为转矩系数,J为惯性系数,由电机结构参数决定。
,km为转矩系数,J为惯性系数,由电机结构参数决定。
当电机空载时,.gif) ,因此有:
,因此有: .gif) (4)
(4)
.gif) (5)
(5)
将(5)式代入(1)式,得:
 (6)
(6)
对(6)式求Laplace变换,得:
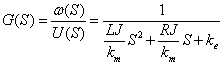 (7)
(7)
(7)式就是无刷永磁直流电机的输出转速与输入电压的传递函数,它是I型系统、二阶系统。
令 ,
,
则(7)式变形为: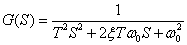 (8)
(8)
其中:T为时间常数,ω0为自然频率,ξ是阻尼比。
3、控制算法设计与求解
基于对无刷永磁直流电机数学模型的研究以及二阶系统成熟的控制理论,采用最为成熟的PID控制算法对其进行控制[2],相应的控制系统结构图[3]如图3所示。
.gif)
图3 控制系统结构图
则其系统闭环传递函数为: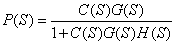 (9)
(9)
此处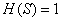 ,并且
,并且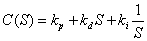
因此有: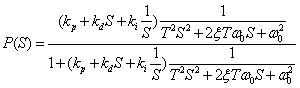 (10)
(10)
对(10)化简并整理,得: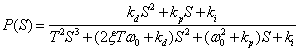 (11)
(11)
基于模型匹配的PID控制器参数设计方法,选择闭环控制系统的标准传递函数为[4]: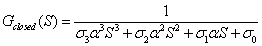 (12)
(12)
其中:σ3、σ2、σ1和σ0为闭环控制系统的标准传递函数;系数α为控制系统自由设计参数。通过α值的不同来平衡控制系统对指令响应和扰动抑制。根据模型跟踪控制的ITAE规则,推荐闭环控制系统的标准传递函数系数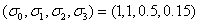 [4]。
[4]。
根据(11)和(12)式,可以计算出: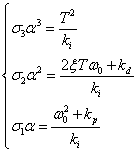 (13)
(13)
解(13),得: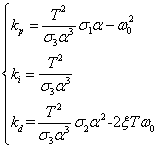 (14)
(14)
4、控制电路的实现
由于目前集成运放的可靠性、稳定性高,价格低廉,因此使用集成运放来搭建控制电路是一种较好的选择。图4给出了使用集成运放实现的PID控制电路。
.gif)
图4 基于集成运放的PID控制电路
由电路原理易知: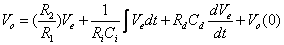 (15)
(15)
即: (16)
(16)
因此,在求得PID的参数后,就可以容易得出电路参数。
5、仿真试验
根据上述的闭环传递函数,在MATLAB下对被控系统进行仿真,得到仿真结果如图5所示。
.png)
图5:对被控系统进行MATLAB仿真结果
由仿真结果可以看出:对于精密仪器中的微型无刷永磁直流电机采用PID控制,在控制精度、快速性、超调量各方面可以取得较好的效果。可以使电机稳定、快速地调速。
6、小结
本文通过对精密仪器中的微型无刷永磁直流电机的数学模型的分析,使用模型参数匹配的设计方法计算出基于PID控制的参数,实现了高精度和低成本的电机控制。
参考文献
[1] 谢帅.直流电机伺服控制系统的设计[J]. 科技资讯, 2010, (3):212-212.
[2] 唐任远.现代永磁电机理论与设计[M]. 北京:机械工业出版社, 1997.
[3] 宋宝等.基于二阶系统的伺服电流调节器的参数整定[J]. 机械与电子, 2004, (9):13-15.
[4] 叶佩青等.基于振动模型的精密工作台运动控制[J]. 清华大学学报-自然科学版,2006, 46(2):206-209.
作者简介:
贺吟涓(1989- )
女,湖南省湘潭市人,清华大学精密仪器与机械学系本科2007级学生。
摘自《自动化博览》2011年第二期





.jpg)




