《自动化博览》

     作者简介

    陈星（1988-），女，湖北仙桃人，硕士，中共党员，现就读于厦门大学 控制理论与控制工程研究所，主要研究方向为图像识别。曾参与过工业控制参数优化项目及项目茶杯茶壶识别项目的研究。 

    摘要：目前检测圆的方法很多，最常用的为Hough变换，另外还有一些改进的Hough变换和圆的快速检测方法，但是这些方法如果直接运用于存在同心圆的图像中，就不能检测出同心圆。目前对同心圆检测的算法较少，而且存在一定局限性，这里提出一种结合圆梯度信息和二次检测圆的新的检测同心圆的算法，改善了检测的局限性，不需要事先确定圆的一些参数仍然能准确检测同心圆，具有一定抗干扰性，且检测速度较快。本文通过实验仿真和应用实例，证明了该算法简单、准确，有效。

    关键词：Hough变换；圆；同心圆；二次检测；梯度

    Abstract: There are several methods to detect circles and Hough transformation is the mainstream method. Besides, Hough transformation has been improved and many rapid detection algorithms have been developed. However, these algorithms cannot detect concentric circles if applied directly. Existing concentric circles detection algorithms are rare and with certain limitations. This paper proposes a novel concentric circles detection algorithm based on circle gradients and secondary circle detection, which improves the limitation and complexity. This algorithm performs some robustness and has certain capability of interference rejection. It can detect concentric circles accurately without requiring apriori knowledge about the circles. Experiments and some applied examples in this paper show that this algorithm is accurate, quick and efficient detecting concentric circles.

    Key words: Hough Transform; Circle; Concentric Circles; Secondary Detection; Gradient

     一些常见的平面规则图形，如直线、圆形、椭圆形、三角形、正方形等在工业产品检测、生物信息提取、集成电路板在线质量检测、交通标志识别等领域等有着广泛的应用[1]。对于直线、圆形等检测问题，已经提出了大量实用的检测方法，但对于同心圆检测问题，目前没有专门的检测算法，部分学者在这一方面做了一定的研究，如文献[2]提出的基于弦中点Hough变换的同心圆检测方法，这种方法虽然能比较好地检测出同心圆，但每次都要重复遍历边缘特征点找到弦中点，当图中同心圆每增加一个，算法复杂度会剧烈增大，这样就不利于对存在很多同心圆的图像进行检测。文献[3]给出了一种同心圆检测中的区域划分算法，在圆心已知情况下用最小二乘法拟合圆，但没有给出具体的圆心计算方法，且仅适合于固定区域划分层次。

    目前，有许多检测圆的算法，Hough变换是检测圆的一种常用方法，由Paul Hough 在1962年提出[4]，它的突出优点是可以将图像中较为困难的全局检测问题转换为参数空间中相对容易解决的局部峰值检测问题[5]。本文将提出一种基于改进的Hough变换的二次检测同心圆的算法，先用一种改进的Hough变换算法检测圆，再将检测到的圆进行破坏后，进行第二次圆检测，最后判断前后检测到的圆的圆心和半径的关系来判断其是否为同心圆。这种算法克服了以前同心圆检测算法缺点，一方面缩小了检测同心圆的局限性，另一方面提高了检测效率，并用仿真和应用实例证明了算法的高效和准确性。
 
    1 改进的梯度Hough变换检测圆(IGHT)

    圆的一般方程为： 

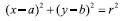        (1)

    在对圆进行检测的时候，往往只需要得到该圆的边界信息，这就要用到边缘检测，一阶导数可以用于检测图像中的一个点是否是边缘点。

      图像 f(x,y)在 (x,y)的梯度定为如下方向：

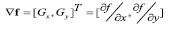      (2)

    梯度向量指向在坐标 的 的最大变化率方向。由向量分析得：

      (3 )

    其中 表示向量 在 处的方向角，角度以 轴为基准度量，边缘在 处的方向与此点的梯度向量的方向垂直[6]。文献[7]提出了一种梯度Hough变换来检测圆方法，用极坐标方程表示圆：
     
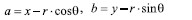  (4)

    在事先知道半径情况下,用求圆边缘上每一点的梯度方向角 和根据边缘点的坐标 来求圆心坐标 ，这样必须预先知道所求圆的半径范围，有较大局限性，所以在此基础上对GHT方法进行改进。

    如图1，圆上所有点的梯度方向都是指向圆心的，圆边缘上所有的法线必相交于圆心。

    传统的Hough变换用三维累加器 累加来求得圆心和半径[8], 图像平面的方程转化为参数平面上的示意图如图2，这样每次检测圆都要遍历整个三维参数空间，耗费大量内存，计算量巨大。为了降低HT方法累加器维数，累加过程分两阶段进行: 第一阶段，遍历图像，求边缘梯度，通过Hough变换在参数空间的二维累加器A累加，通过累加的局部峰值确定圆心，第二阶段，再遍历图像边缘点，用一个一维累加器B累加半径，出现频率最高的半径作为此圆心对应半径。
   
                             
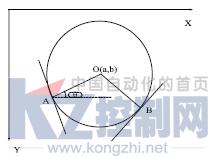
                             图1 圆心位于圆边缘点法线交点 
  
            
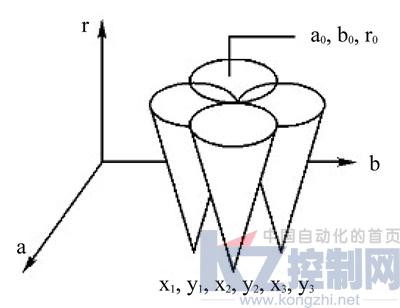
                             图2 圆的Hough参数空间

    2 基于IGHT的二次检测的同心圆检测算法

    改进的梯度Hough(IGHT)变换方法的优点是图像中存在圆交叉、圆互相包含等情况时，仍能检测出圆，但是当有同心圆时，只能检测出同心圆中最小的一个。如图3所示。
       
                  
                                     (a)原图                   (b)检测结果

                       图3 IGHT检测到的同心圆中的小圆

      基于此，本文提出先用IGHT方法进行第一次圆检测检测到小圆，记录圆心(x₁,y₁ )，和半径r₁ 。对此圆进行破坏，分割出外圆，再使用IGHT进行第二次Hough圆检测，再次记录圆心 和半径 。定义距离：  

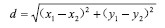    (5)

      根据圆与圆的位置关系，当d