- 企业简介
-
《自动化博览》立足于整个中国自动化产业,加强报道国家政府及相关部门针对自动化行业的政策、专项及相关发展规划。促进行业交流、引领产业发展,《自动化博览》立志于成为中国自动化领域中集实用技术与权威信息为一体的专业传媒。
- 公司类型:其他
- 联系方式
-
- 《自动化博览》
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116290
- 传真:59813329
- 网址:http://www.kongzhi.net
- Email:bjb@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 模糊控制在真空环境模拟试验舱温控系统中的应用 技术领域 运动控制 行业 航空航天 简介 内容 摘要:对某真空环境模拟试验舱原有温控系统的半开环的结构进行闭环改造并研制新的控制算法,改善系统的动态性能;在对被控舱内温度进行建模分析的基础上,探讨了PID控制器、基本模糊控制器和模糊-PI复合控制器三种控制器的设计方法以及在温控系统中的实现,并通过常规变温试验和模拟脉冲干扰试验对三种控制器进行比较。
关键词:PID控制;模糊控制;复合控制;自调整因子;误差预测
Abstract: This article is to change the half-open structure into closed loopstructure and to develop a new controller to promote dynamic characters of thesystem . Based on the analysis of the temperature model of the simulator, thedesign and realization of PID, Fuzzy and Fuzzy-PI controller are discussed. Threecontrollers are compared through ordinary poikilothermia and pulse interfereexperiments..
Key words: PID controller; Fuzzy logic controller; Fuzzy-PI synthetic controller; Selfadjustingfactor; Error prediction
1 前言
某真空环境模拟试验舱主要功能是模拟外太空空间高真空环境及其温度变化,目的是为检验部分暴露于真空环境的航天装船产品的性能和可靠性,该模拟主要指标如下:真空度要求达到1×10-3Pa以下,舱内壁(夹套)的温度在-30℃~+70℃范围内可调,并能实现梯形交变温度循环,稳态控制精度为±1℃,平均温度变化率不小于1℃/min。该舱原温控系统工作原理是采用蓄冷、蓄热式工作原理,通过液体载冷剂在舱体内套循环管路中的循环来调节舱内温度,由智能仪表分别控制热媒管路或冷媒管路以及循环管路的液体流量(阀门开度)来调节温度,阀门均为电动调节阀。在实际应用中由于设备自身的大滞后特点,控制效果并不好,尤其是在动态响应过程中,过程过渡阶段曲线不够理想,超调量较大,需有经验的操作人员运用其专家知识手动补偿给定以满足指标要求,因此决定在不改变系统基本硬件配置的基础上,增加一多功能数据采集卡,实现指标闭环控制的计算机控制系统,由计算机作为主控单元,重新研制控制算法,并通过试验研究对三种控制方法进行比较,在满足指标基础上提高控制精度和自动化程度。
2 硬件配置
原温控系统中控制调节功能由智能仪表(EUROTHERN902)完成,控温点设在媒体三通混合器的出口处,而不是在设计指标要求的舱内壁,而计算机所记录和显示的温度是舱内壁温度。硬件设计的具体方法是在舱内筒型空间均匀分布六个温度传感器,将采集的六路温度值经A/D转换后送入计算机,经过加权均值滤波后取平均值作为系统的反馈温度值,经计算机推理计算后得出控制输出量,通过串口通讯的方式控制系统原有智能仪表——欧陆表输出通道输出量,经PLC直接控制电动调节阀门动作,改进后的系统结构如图1所示。
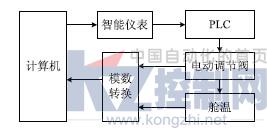
图1 系统硬件结构图
实际硬件部分的设备分别是:计算机为联想品牌机, A/D转换板采用研华PCL-812PG多功能数据采集卡。软件编程环境Microsoft Visual C++ 6.0可视化编程环境。
3 对舱温系统的建模分析
舱温对象实际上就是一个温度过程对象,其对象特性可以用一个带纯滞后一阶惯性环节来表示[1]:
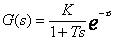 (1)
(1)
式中:K是放大系数,即稳态时输入与输出幅值之比。
T是时间常数,即输出值从起始值到稳态目标值的63%所需时间。τ为纯滞后时间。
我们采用阶跃响应法,又称飞升曲线法来求得上述惯性环节的参数可近似得纯滞后时间τ=240s,时间常数T = 1080s,则系统模型为
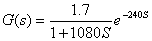 (2)
(2)
4 算法比较
数字PID控制器在连续时间控制系统中,PID控制器应用的非常广泛,我们采用PID的“增量算法”对系统进行控制,其描述离散时间差分方程如下[2]。
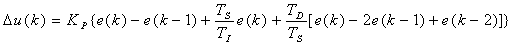 (3)
(3)
由系统模型根据经验公式可求出PID控制中的参数:控制周期:TS=0.05τ;比例增益;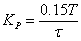 ;积分时间常数;TI=2.0τ;微分时间常数;TD=0.45τ。从而可计算出TS=12,KP=0.67,TI=480,TD=108。由于用飞升曲线法估计的模型与实际系统之间存在一定的偏差,因此在估计模型参数的基础上采用经验调试方法[3],即按照先比例,再积分,后微分的整定步骤得出的参数为KP=0.58,KI=0.22,KD=0.4。PID控制结果数据如下:上升时间:38分30秒;超调量:3.41℃;稳定时间:41分13秒;稳态误差:±0.37℃。
;积分时间常数;TI=2.0τ;微分时间常数;TD=0.45τ。从而可计算出TS=12,KP=0.67,TI=480,TD=108。由于用飞升曲线法估计的模型与实际系统之间存在一定的偏差,因此在估计模型参数的基础上采用经验调试方法[3],即按照先比例,再积分,后微分的整定步骤得出的参数为KP=0.58,KI=0.22,KD=0.4。PID控制结果数据如下:上升时间:38分30秒;超调量:3.41℃;稳定时间:41分13秒;稳态误差:±0.37℃。
模糊控制器 考虑采用一种不需建立精确的数学模型又有一定的抗干扰能力的控制方法,即模糊控制方法。首先各个I/O论域离散化取13个0和0左右的正、负整数,即{–6,–5,…,–1,0,1,…,5,6}。接着对I/O空间进行模糊划分,划分为7个左右等级,正大(PB),正中(PM),正小(PS),零(ZO),负小(NS),负中(NM),负大(NB)。模糊推理采用Mamdani推理合成方法[4],即取大-取小(-)法,解模糊方法采用重心法。采用基本FLC在舱温控制系统中进行试验。在实际设计中,模糊控制器的输入语言变量选为实际温度y与温度设定值r之间的误差e=r-y及其变化率ec,输出语言变量为控制热媒流量的电动调节阀开度增量u,因此系统为一双输入单输出系统,如表1所示。
温差e的基本论域设为[-6℃,+6℃],将论域归一化为13个整数元素的离散集合X ={-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6},则得误差e的量化因子Ke=1, e>6则E=PB,e<-6则E=NB,每个语言值作为一个模糊变量,对应一个模糊子集合。同理温差变化率基本论域为[-3℃/min,+3℃/min],选定EC的论域Y={ -6,-5,…-1,0,1,…,5,6},误差变化率ec的量化因子Kec=2。电动调节阀的开度增量论域为[-12%,12%],选定U的论域Z={ -6,-5,…-1,0,1,…,5,6},增量输出u的解模糊比例因子Ku=2。通过总结经验得出控制规则表1。试验结果曲线如图2所示,数据如下:上升时间:27分46秒;超调量:1.5℃;稳态误差:1.3℃;振荡周期:30分15秒。
表1 基本模糊控制器规则表
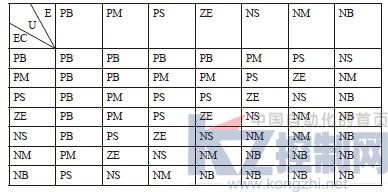
图2 基本模糊控制器试验曲线
模糊复合控制器 基本FLC的稳态误差无法消除,有明显的缓慢振荡,原因之一是在模糊化过程中进行了四舍五入取整运算,为了弥补基本FLC的不足,采用Fuzzy和PI相结合的Biakowskif法复合控制方式。出发点是在模糊比例和微分作用中加入积分作用,调节稳态特性[5]。我们根据设计指标中稳态精度要求,设定切换阀值E为ZE,即当误差e对误差模糊语言值ZE的隶属度大于等于0.7时,加入PI控制,否则为 Fuzzy控制。
常规的模糊控制器在设计过程中模糊控制规则可用解析式表示如下[6]:
U=-<(E+EC)/2>
可看出,控制作用取决于误差和误差变化,且二者处于同一加权程度。事实上,对于不同的控制对象或控制系统响应过程的不同阶段,要求误差和误差变化率分别对系统输出控制量有不同的影响。我们采用一种更简便、实用的在整个论域范围内根据误差的大小自动调整的Fuzzy控制。则在整个论域范围内在线自调整参数的Fuzzy控制规则可表达为
U=-<αE+(1-αEC)/2> α∈[0,1] (4)
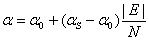 (5)
(5)
其中α∈[α0 ,αS],0<α0<αS<1,在本课题中α0取0.3,αS取0.9。上述控制规则的特点是:调整参数在α0和αS之间随着误差绝对值|E|的大小而呈线性变化,因N为量化等级,故α有N个可能的取值,当误差较大时,对误差的控制作用给予较大的权重,以尽快消除误差,提高响应速度;当误差较小时,为避免系统响应超调,对误差变化的控制作用给予较大的权重,以尽快进入稳态。那么将带自调整因子的Fuzzy-PI控制规则用解析形式表示如下:
u=u+Δu
 (6)
(6)
为从根本上解决系统大滞后问题,我们在系统中引入预测控制,为在t时刻得到合适的控制量u(t),则必须预测出过程在t+ 时刻的输出y(t+ ),然后再计算预测偏差e及预测偏差变化ec,再对e、ec Fuzzy量化,通过推理合成和Fuzzy决策,得出控制量u(t),从而做到了“提前控制”,而不是“事后控制”,这会使系统的鲁棒性大大增强[7]。对于无滞后的单输入单输出系统,设y(t)为被控量,u(t)为控制量,通过采样得到的过程的输入、输出序列,总存在一个连续可微函数f可以精确描述y与u的关系,即y(k) = f(u(k)),其中k = 0,1,2,…。其采样值y(k+1)可用当前时刻采样值y(k)附近的一阶Taylor展开式近似得到,即:
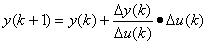 (7)
(7)
若设被控量与控制量的增量之比(即动态增益)为M(k)=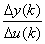 ,若单输入单输出系统的纯滞后步数为L>0(其中L =
,若单输入单输出系统的纯滞后步数为L>0(其中L = ,为过程的纯滞后时间,T为采样周期),得到L步预测模型:
,为过程的纯滞后时间,T为采样周期),得到L步预测模型:
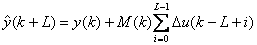 (8)
(8)
本课题中,由飞升曲线得滞后时间约为4分钟,我们取控制周期T为2分钟,则滞后步数L=2,阀值取0.5,当|Δu|≥ ,预测模型为下式
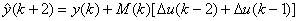 (9)
(9)
其中 。为防止Δu过小产生计算值无穷大,当|Δu|< 时,预测模型采用式(10)。
。为防止Δu过小产生计算值无穷大,当|Δu|< 时,预测模型采用式(10)。
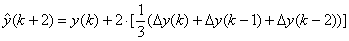 (10)
(10)
可得预测误差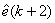 和预测误差
和预测误差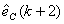 变化率:
变化率:
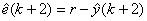 (11)
(11)
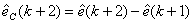 (12)
(12)
影响模糊控制器性能的一个不可忽略的因素是系统比例因子(量化因子)的选择,它们对系统的动态性能具有较大的影响[8],模糊控制同常规PID控制一样,其动、静态特性之间存在一定的矛盾,需要根据系统的误差和误差变化率等信息对控制器的参数进行在线修正。我们采用在线调整Ku的方法,为简化控制算法,采用分段调整Ku的方法。在初始升温或降温阶段,温差较大,采用较大的Ku;接近希望值时,要求控制动作细腻一些,采用较小的Ku;如果温差变化趋势增大,则增大Ku,反之,则减小Ku。带误差预测和自调整因子的Fuzzy-PI复合控制器系统原理框图如图3所示。

图3 Fuzzy-PI复合控制器系统原理框图
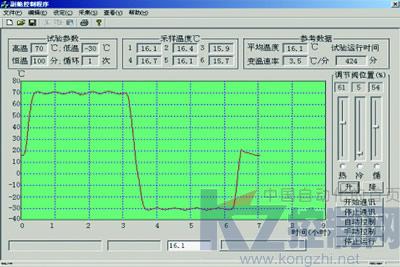
实际的试验曲线如图4所示,系统主要的动态和静态指标如下:上升时间:31分23秒;超调量:0.8℃;稳态误差:0.53℃;
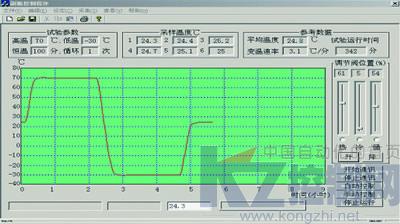
图4 Fuzzy-PI复合控制试验曲线
5 抗干扰能力比较
评价系统是否性能优良的一个重要指标是系统的抗干扰能力,我们采取了模拟脉冲输入的方法进行试验,以比较三种控制方法的鲁棒性。具体做法是将目标温度设为40℃,首先采用Fuzzy-PI复合控制方式将温度升到目标值,当系统温度达到稳态并恒温一段时间后,打开舱门30秒然后关闭以模拟脉冲干扰,在系统重新回到稳态后切换控制方式到PID控制器进行模拟干扰试验,待PID控制曲线重新回到稳态平衡后再切换到基本Fuzzy模式进行模拟干扰试验,以观察三种控制器的响应曲线。试验曲线如图5所示。由图可见三种方式对脉冲扰动反应都比较强烈,但Fuzzy-PI复合控制器恢复平衡的时间短,温度拐点曲线平缓,无超调、无振荡;PID控制器产生了较大的超调,导致其稳定时间较长,但系统稳定后精度较高;基本FLC则对控制量校正迅速,也无超调,但在目标值附近的极限环振荡无法消除。
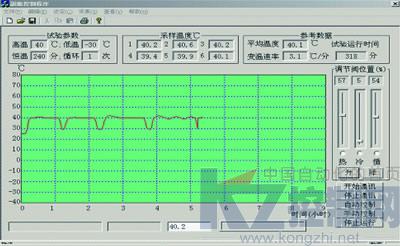
图5 模拟脉冲干扰试验曲线
6 性能指标比较
下面给出三种控制方式的主要性能指标对比。
表2 性能对比(常规控制试验)
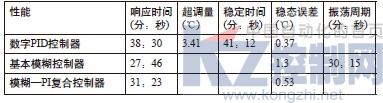
表3 性能指标(干扰模拟试验)
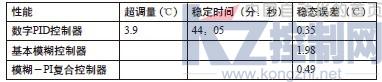
从三种控制方式的常规试验和扰动试验结果来比较和分析如下:
(1)PID控制器上升时间较长,在响应过程中产生较大的超调量,稳定时间长,无稳态误差,对扰动的反应存在较明显的滞后性,恢复时间较长。
(2)基本FLC响应过程中由于只有模糊比例和微分作用,响应速度和对扰动的反应较快,但稳态过程中存在极限环振荡。
(3)加入误差预测和自调整因子的Fuzzy-PI复合控制器在动态过程中模糊比例起主导作用,接近目标值时微分作用起主要作用,因此响应速度快,且无超调,对扰动反应迅速,恢复时间也短,而在稳态过程中加入积分作用则快速消除了稳态误差。
7 结论
可见经典PID和基本FLC由于其各自算法上都有一定的不足之处,而加入了误差预测和自调整因子的模糊-PI复合控制器很好地结合了基本FLC和传统PID控制的优点,在动态和稳态特性综合性能指标上优于单独的基本FLC或PID控制器。本次改造项目在实际应用中效果良好,在保证了控制精度基础上系统自运行能力和鲁棒性大大提高。
参考文献:
[1] 黄一夫. 微型计算机控制技术[M]. 北京: 机械工业出版社, 1988.
[2] 沈春霖, 吴厚宜等. 数字控制系统-原理、硬件与软件[M]. 北京: 航空工业出版社, 1993.
[3] 张宇河, 金钰. 计算机控制系统[M]. 北京: 北京理工大学出版社, 1996.
[4] 王立新. 模糊系统与模糊控制[M]. 北京: 清华大学出版社, 2003.
[5] 章卫国, 杨向忠. 模糊控制理论与应用[M]. 西安: 西北工业大学出版社,2000.
[6] 龙升照, 汪培庄. Fuzzy控制规则的自调整问题[J]. 模糊数学, 1982, (3):5-112.
[7] 徐福仓, 申群太, 黄海悦. 预测控制在大滞后电阻炉系统中的应用研究[J].自动化学报, 2000, 9(3): 19.
[8] 诸静. 模糊控制原理与应用[M]. 北京: 机械工业出版社, 2001.
赵维(1972-)男,吉林长春人,控制理论与控制工程专业硕士学位,高级工程师,长期从事航天环境模拟技术和模拟设备的研制工作,现就职于中国航天员科研训练中心,主要从事智能控制理论与技术、PLC技术及应用、现场总线、机电一体化等方面的研究。
毕建智(1965-)男,山东威海人,航天试验指挥专业硕士学位,高级工程师,现就职于中国航天员科研训练中心,长期从事航天环境模拟技术和模拟设备的研制工作,主要从事人工大气环境模拟、机械工程理论与设计等方面的研究。
摘自《自动化博览》2011年第八期





.jpg)



.png)
