《自动化博览》

    摘要：针对Boost变换器中负载的不确定性或干扰不满足匹配条件的情况，设计了鲁棒反步滑模控制器，可使Boost电路的输出电压快速达到期望值，且稳态误差很小。最后用仿真结果验证了本文所提方法的可行性。

    关键词：反步滑模控制；Boost变换器；鲁棒性

    1 引言

    在DC-DC变换器的控制问题中，变结构控制虽然具有良好的鲁棒特性，但它要求系统的不确定性或干扰满足匹配条件。当干扰或不确定性不满足匹配条件时，反步控制方法则具有明显的优越性。将反步法与滑模控制方法相结合就可以很容易的处理带有不满足匹配条件的不确定性和扰动。文献^[1]针对Boost变换器负载的不确定性设计了反步滑模控制器，文献^[2]针对Buck变换器的负载不确定性设计了自适应反步滑模控制器。笔者针对Boost变换器的负载的不确定性，设计鲁棒反步滑模控制器，并分析了系统的误差范围。

   2 Boost变换器的平均模型

   Boost变换器又称升压变换器^[3]，Boost电路图如图1所示。
            
                       
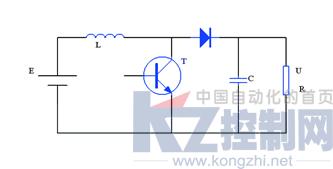
                                  图1 Boost变换器电路

    设电容电压为x₁，电感电流为x₂，u为保持开关周期T不变时调节开关导通的时间t与开关周期T的比值。一般情况下，由于T很小，定义平均电容电压和电感电流为：

          
    

    v_d 和i_d  为Boost电路的输出电压和电感电流。

    3 鲁棒反步滑模控制器设计

    Boost 变换器的平均模型(2)式重新记为下式。

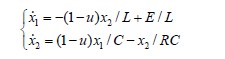                      (3)

     其中  x ₁表示电容电压，也就是输出电压，  x₂ 表示电感电流，负载为R 。由于实际电路中负载存在不确定性，假设实际电路中负载满足等式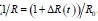   ， R ₀  表示负载的标称值， ΔR(t )表示负载的不确定项。由于Boost电路是非最小相位系统，跟踪目标不能直接设定为期望输出电压。而是跟踪系统达到平衡时的稳态电流  I _d 其表达式如(4)，Boost电路的平衡点为 。

             

                                           
               
      
       
     
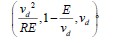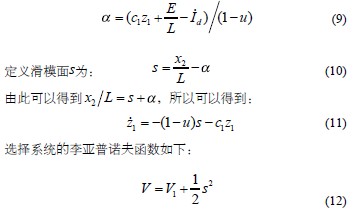
     4 仿真研究

     为了验证上述反步滑模控制器的效果，选取的Boost电路参数为负载电阻R = 30Ω，并假设存在不确定性ΔR = −5Ω，输入电压E =15V，电感 L=20mH , 电容C=68u F，v_d =25V d v 。控制器的参数选为， C ₁ =100，  C ₂ = 50， k =1，p = 0.01。
  
                        
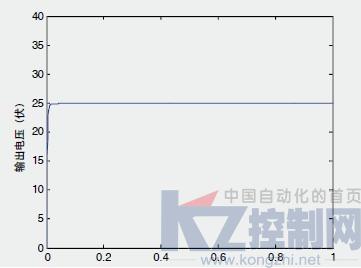
                                        图2   系统响应输出电压  

                       
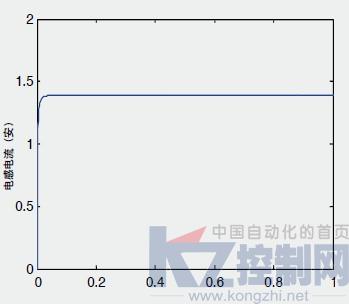
                                          图3   系统响应电感电流 

                     
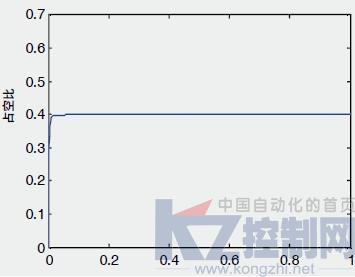
                                            图4    系统占空比

    5 小结

    由仿真图可以看出系统Boost变换器的状态在很快的时间内到达了平衡点，而且在负载R存在不确定性的情况下系统的稳态误差非常小。

   参考文献：

   [1] El Fadil, H. Giri, F Ouadi, H. Adaptive sliding mode control of PWMboost DC-DC converters[C], Computer Aided Control System Design,2006 IEEE International Conference on Control Applications, 2006 IEEEInternational Symposium on Intelligent Control, 2006 IEEE, 4-6 Oct. 2006Page(s):3151-3156.

   [2] Li-kui Yi, Jim Zhao, Dan Ma. Adaptive Backstepping Sliding ModeNonlinear Control for Buck DC/DC Switched Power Converter[C], Controland Automation, 2007. ICCA 2007.IEEE International Conference, May 302007-June 1 2007:1198 – 1201.

    [3] 吴爱国, 李际涛. DC-DC变换器控制方法研究现状[J], 电力电子技术,1999, (2): 75-78.

     何墉助教，现就职于洛阳理工学院电气工程与自动化系。李春娟讲师，现就职于洛阳理工学院电气工程与自动化系。    

    摘自《自动化博览》2012年第一期