《自动化博览》

    摘要：传统的小波分解存在小波基函数难以选择的问题，经验模式分解（EMD）存在模式混叠现象，不能准确地诊断出轴承故障。因此本文将集成经验模式分解（EEMD）和能量算子解调相结合，建立了滚动轴承单自由度模型，仿真故障激励，以获取轴承故障动力学响应。最后利用模型结果对本文方法进行数值验证，以证明本文所提方法的有效性和正确性。

    关键词：EEMD；能量算子解调；滚动轴承；故障诊断

    Abstract: Rolling bearing fault is difficult to diagnosis accurately because the basis function is difficult to select in the conventional wavelet decomposition and the pattern aliasing exists in theEMD method. Thus, this paper proposes a method to combine EEMD and energy operator demodulation. It builds a single degree of freedom model for the rolling bearing to simulate the stimulus of faults, so as to obtain the dynamic response of bearing fault.   Finally, the proposed method is verified via the model’s numerical results to prove its effectiveness. 

    Key words: EEMD; Energy operator demodulation; Rolling bearing;   Fault Diagnosis

    滚动轴承故障诊断方法常分为平稳信号法和非平稳信号法，其中平稳信号法应用广泛，包含时域法和频域法。时域方法中，常将统计参数法作为时域方法中最有效的方法。统计参数主要包含有量纲指标和无量纲指标两大类。时域方法是一种很好的特征提取方法，但不能分辨出故障类型。频域分析方法是从整个频域上对振动信号进行处理，不能针对包含故障冲击的特定频带进行高分辨率分析，不能克服谐波分量对故障冲击特征提取的影响问题。在时频域信号处理方面，小波分析作为一种时频域分析方法，具有多分辨率等优点。但小波分析和频域分析方法一样，仍是一种基于基函数的分析方法，经小波分解后的每个分量失去了物理意义[1]。经验模式分解（EMD，Empirical Mode Decomposition）得到了广泛应用，该方法采用基于信号自身的自适应广义基，避免了小波基函数的选择，同时是一种很好的自适应分解方法。但EMD分解易存在频率混叠现象，因此Huang提出了集成经验模式分解（EEMD，Ensemble Empirical ModeDecomposition)信号分解方法[2]。Y Lei将EEMD引入到滚动轴承故障诊断中，并取得了良好的效果[3,4]。Z.K. Peng等利用EEMD相对于EMD的优势以改进HHT，并和基于小波包的时频分析在振动信号处理中做了比较[5]。能量算子解调[6]可以对单分量调幅调频(AM—FM)信号进行解调，并能有效计算信号的瞬时幅值和瞬时频率，特别适用于处理信噪比较高、瞬时频率变化较缓慢的信号，主要用于提取单分量调幅调频信号的幅值包络和瞬时频率，在语音信号、图像处理等领域得到了广泛的应用。因此本文在EEMD分解的基础上，对分解后的结果进行能量算子解调分析，最后利用谱分析得出诊断结果，并建立滚动轴承单自由度模型以对本文方法进行数值分析验证。

    1　EEMD算法

    EEMD是一种噪声辅助的信号分解方法，通过在原始信号中添加白噪声并对其进行EMD分解，最后利用多次分解后的结果进行集总平均计算。

    EEMD算法流程如下：

    （1）向信号x(t)加入正态分布白噪声。

    （2）将加了白噪声的信号经EMD分解成各IMF分量 , im c ，其中i=1，2，. . . N，m=1，2，. . . M； N为IMF的个数，M为加入噪声的次数。

    （3）重复步骤(1)~(2)，每次加入新的白噪声序列nm(t)。

    （4）将每次EMD分解得到的IMF集总均值作为最终结果：

    
    
    2　能量算子解调

    

    离散信x (t)的能量算子解调可定义为

     

    可见，每一瞬时时刻能量算子解调的计算只需要三个采样点，故该方法具有良好的瞬时性。

    进而能得到(xt)的瞬时幅值和瞬时频率估计量。

    

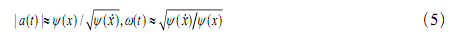
    此时，信号(xt)的幅值(at)和频率(tω)的估计就可以由信号能量函数(xψ)和和信号微分能量函数(xψ)确定。

    3　滚动轴承单自由度仿真模型

    将滚动轴承仿真模型简化为一个单自由度的线性模型，如图1所示，m为轴承系统的质量，c为轴承的阻尼，k为轴承的刚度， δ为由于故障引起的一定频率的脉冲力，x为轴承的振动响应。以外圈发生疲劳剥落故障情况为例，首先从单个脉冲情况分析，假设t = 0时刻有一个由于故障引起的单位脉冲力 δ，分析如下：

                      
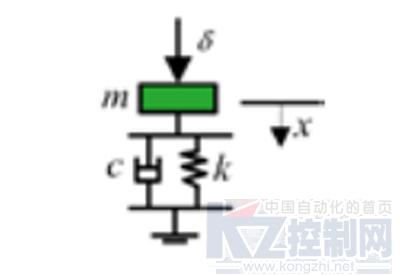
                                       图1 单自由度模型

    记0-、0+分别为单位脉冲力作用瞬间的前后时刻，单自由度系统的运动微分方程与初始时刻可合写为：

    

    解方程，可得单自由度线性振动模型的通解为：

    
    
    以上为单冲击信号，在滚动轴承故障时，每经过一个故障位置就会产生一个冲击，而每个冲击之间的时间即为故障特征周期，相对应则有一个故障特征频率，该冲击频率也为调制频率。

    4　数值验证

    为验证本文所提方法的有效性和正确性，首先采用数字仿真故障信号 (x)t 和正常信号 (x) ′t ，其中 y(t)模拟滚动轴承故障产生的冲击响应信号，调制频率 fr为10Hz，共振频率(有阻尼固有频率)为500Hz，同时还包含150Hz和90Hz的谐波成分， () nt 为白噪声。采样频率设置为2000Hz，采样点数设置为5120。

    

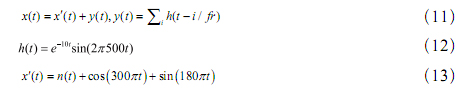
    x(t)时域波形如图2所示。对其进行EEMD分解（图3）。

    由图3看出，90Hz、150Hz的正常状态下的频率成分信号和500Hz的故障调制信号被有效地分解出来，同时没有发生频率混叠。对第一个imf进行能量算子解调谱分析，结果如图4所示，可见

                 
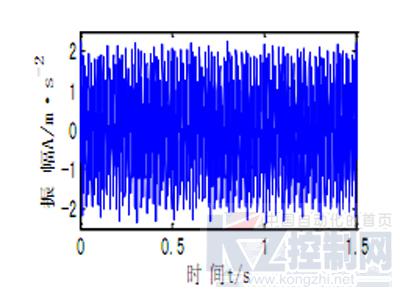
                                         图2   (x)t时域波形图

                
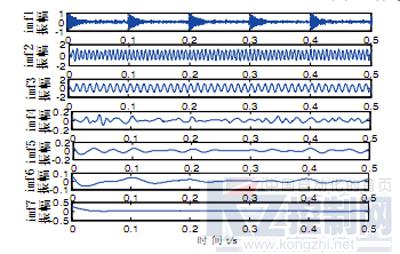
                                图3 EEMD分解效果图(振幅：m-s-2)
 
    故障频率10Hz及其倍频成分明显，证明了本文方法是有效可行的。

                
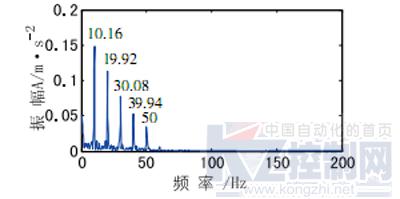
                                  图4 仿真信号的能量算子解调谱

    5　结束语

    针对滚动轴承故障诊断问题，本文建立了滚动轴承单自由度模型，构建了数值仿真数据。相对于传统的小波分析和Hilbert解调，本文应用了自适应分解方法EEMD，并结合能量算子解调对EEMD分解的结果进行分析，提高解调精度以准确判断故障。并通过建立的仿真数据对本文的方法进行了验证，充分验证了该方法的有效性，为滚动轴承的工程应用和诊断提供理论参考。

    参考文献：

    [1] 郭代飞, 高振明, 张坚强. 利用小波门限法进行信号去噪[J]. 山东大学学报, 200l, 36 (3) : 306-311．

    [2] Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1 (1) : 1-41.

    [3] Y Lei , MJ Zuo, MHoseini . The use of ensemble empirical mode decomposition to improve bispectral analysis for fault detection in rotating machinery[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2010, 224 (8) : 1759-1769.

    [4] Yaguo Lei, Zhengjia He,Yanyang Zi. EEMD method and WNN for fault diagnosis of locomotive roller bearings[J]. Expert Systems with Applications, 2011, 38 (6) : 7334-7341.

    [5] Z.K. Peng, Peter W. Tse, F.L. Chu. An improved Hilbert–Huang transform and its application in vibration signal analysis[J]. Journal of Sound and Vibration, 2005, 286 (1) : 187-205.

   [6] 李辉, 郑海起, 杨绍普. 基于EMD和Teager能量算子的轴承故障诊断研究

    [J]. 振动与冲击, 2008, 27 (10) : 15-18.

    作者简介

    杨旸（1978-），男，湖北宜昌人，工程师，主要研究方向为结构设计。