- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 延迟焦化精馏塔鲁棒控制器设计 技术领域 工厂信息化 行业 简介 本文介绍了基于线性矩阵不等式处理方法的鲁棒控制理论的相关概念和设计控制器时的求解方法,并设计了精馏塔鲁棒控制器。仿真结果表明,文中设计的精馏塔鲁棒控制器,控制效果良好。 内容
引言
在炼油厂延迟焦化装置,保持主精馏塔的操作稳定, 特别在焦炭塔波动时,是关键控制目标。由于延迟焦化工艺的分批进料特性,当一个焦炭塔正在进料而另一个焦炭塔准备焦化时,主精馏塔受到影响很大的瞬时干扰支配。因此,设计性能优越的控制器,改善主精馏塔的操作稳定性就成了目前炼油装置先进控制研究的重要课题。
所谓鲁棒控制,就是设计一种控制器,使得当系统存在一定程度的参数不确定性及一定限度的未建模动态时,闭环系统仍能保持稳定,并保持一定的动态性能品质。由于炼化装置是一个复杂的动态系统,其中存在着各种不确定因素的干扰,而且炼化装置具有很强的非线性,要实现精确建模很不容易,因此,基于鲁棒控制理论的炼化装置控制器设计成为了炼化装置先进控制研究中的热点问题。
对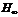 控制问题,存在许多种求解方法,现在经常使用Riccati方程处理方法以及线性矩阵不等式(LMI)求解方法。
控制问题,存在许多种求解方法,现在经常使用Riccati方程处理方法以及线性矩阵不等式(LMI)求解方法。
在近几年内,由于线性矩阵不等式(LMI)的优良性质以及解法的突破,使其在控制系统分析和设计方面得到了广泛的重视和应用。在此之前,绝大多数的控制问题都是通过Riccati方程或其不等式的方法来解决的。但是解Riccati方程或其不等式时,有大量的参数和正定对称矩阵需要预先调整。有时,即使问题本身是有解的,也找不出问题的解。这给实际应用问题的解决带来极大不便,而线性矩阵不等式方法可以很好地弥补Riccati方程方法的上述不足。在解线性矩阵不等式时,不需要预先调整任何参数和正定对称矩阵。因此采用LMI方法设计控制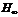 器有很多的优点。
器有很多的优点。
1、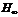 控制问题的线性矩阵不等式(LMI)解法介绍
控制问题的线性矩阵不等式(LMI)解法介绍
在鲁棒控制中,系统描述如下: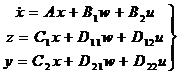
(1)
其中:
将控制器(2)应用到系统(1)后得到的闭环系统是

2、基于LMI解法的延迟焦化精馏塔鲁棒控制器的设计
2.1 延迟焦化装置工艺流程
如图1所示延迟焦化系统: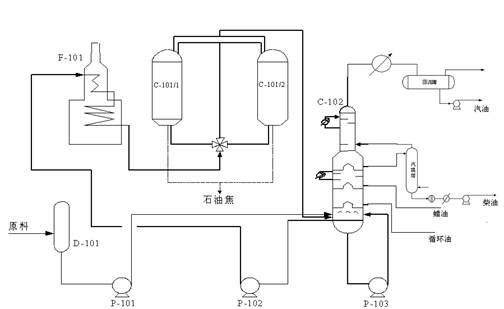
图1 延迟焦化系统模型
原料油(减压渣油)经换热及加热炉对流管加热到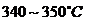 ,进入分馏塔下部,与来自焦炭塔顶部的高温油气(
,进入分馏塔下部,与来自焦炭塔顶部的高温油气(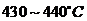 )换热,一方面把原料油中的轻质油蒸发出来,同时又加热了原料(约
)换热,一方面把原料油中的轻质油蒸发出来,同时又加热了原料(约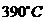 )及淋洗下高温油气中夹带的焦末。原料油和循环油一起从分馏塔底抽出,用热油泵送进加热炉辐射室炉管,快速升温至约
)及淋洗下高温油气中夹带的焦末。原料油和循环油一起从分馏塔底抽出,用热油泵送进加热炉辐射室炉管,快速升温至约 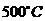 后,分别经过两个四通阀进入焦炭塔底部。热渣油在焦炭塔内进行裂解,缩合等反应,最后生成焦炭。焦炭聚结在焦炭塔内,而反应产生的油气自焦炭塔顶逸出,进入分馏塔,与原料油换热后,经过分馏得到气体、汽油、柴油、蜡油和循环油。
后,分别经过两个四通阀进入焦炭塔底部。热渣油在焦炭塔内进行裂解,缩合等反应,最后生成焦炭。焦炭聚结在焦炭塔内,而反应产生的油气自焦炭塔顶逸出,进入分馏塔,与原料油换热后,经过分馏得到气体、汽油、柴油、蜡油和循环油。
2.2 精馏塔的数学模型
严格来讲.精馏塔的数学模型为复杂的高阶非线性的数学模型。此模型由于形式复杂,非常不适合优化控制器的设计和求解。工程上常用的方法是:在扰动不大的范围内,用低阶线性化模型近似替代高阶非线性模型来进行系统分析和系统设计。 本文选择状态变量物理意义明确的分段集结法对系统进行降阶简化,然后再线性化得到精馏塔的低阶线性化数学模型.并以此作为优化设计的控制模型,某模型塔的非线性数学模型经简化和线性化后为3阶线性化模型,形式如下:

2.3基于LMI解法的鲁棒精馏塔控制器的设计
对于线性矩阵不等式的具体求解,matlab开发了专门的求解工具箱(LMI工具箱)。由于线性矩阵不等式(4)是矩阵变量X,W的一个线性矩阵不等式,因此可以应用LMI工具箱中的求解器feasp来求解该线性矩阵不等式。进而如果该线性矩阵不等式有可行解,则可用dec2mat函数求得可行解X,W,则可构造精馏塔系统的一个状态反馈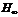 控制器。
控制器。
应用matlab提供的LMI工具箱中的feasp,和dec2mat求得:
应用matlab中的spol函数可以求得设计的反馈系统的极点为
可见设计的系统稳定,应用splot函数可以得出系统的脉冲响应曲线和波特图。如下:
2.4、仿真结果
在一定压强下,混合物的泡点和露点都取决于混合物的组成,因此可以用容易测量的温度来预示塔内组成的变化,通常用塔顶温度反应馏出液组成。所以控制了塔顶温度就可以保证良好的产品质量。当进料发生扰动时,包括进料温度或者进料成分发生变化时,将对精馏塔的塔顶温度和产品质量产生很大的影响。下图给出了在有鲁棒控制器的精馏塔系统中当进料发生不同程度扰动时塔顶温度的变化量。
当扰动是进料扰动其变化量为-20% ,延续时间为15秒脉冲扰动时,塔顶温度的变化量。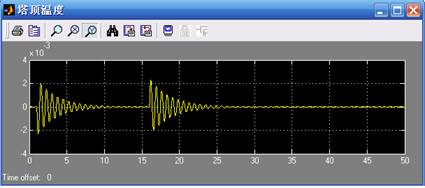
图4 塔顶温度的变化量当扰动是进料扰动其变化量20% ,延续时间为30秒脉冲扰动时,塔顶温度的变化量。
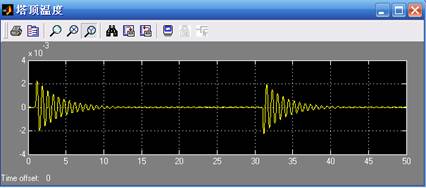
图5 塔顶温度的变化量
2.5仿真结论
当扰动量变化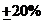 ,并有一定延迟时间,塔顶温度和蒸发段温度经过很短时间过渡到稳定点。说明所设计的鲁棒控制器具有良好的鲁棒性。
,并有一定延迟时间,塔顶温度和蒸发段温度经过很短时间过渡到稳定点。说明所设计的鲁棒控制器具有良好的鲁棒性。3、结论
本文以基于线性矩阵不等式解法的鲁棒控制理论为基础,介绍了线性矩阵不等式的基本概念和鲁棒控制器的设计原理,设计了精馏塔的鲁棒控制器。通过仿真,可以得出以下的结论:
1. 精馏塔鲁棒控制中考虑了扰动的影响,将进料扰动看作是精馏塔的一个 “扰动”,由此设计鲁棒控制器可以更好地抑制由于焦炭切塔而精馏塔进料的变化。
2. 利用Matlab提供的工具箱,可以更方便进行求解和仿真。仿真结果表明基于线性矩阵不等式的鲁棒控制器的控制效果良好,具有工程应用价值。
参考文献
[1] 梅生伟,申铁龙,刘康志. 现代鲁棒控制理论与应用. 北京:清华大学出版社,2003.
[2] 俞力. 鲁棒控制-线性矩阵不等式处理方法. 北京:清华大学出版社,2002.
[3] 程云鹏. 矩阵论. 西安: 西北工业大学出版社, 2002.
[4] 林世雄. 石油炼制工程. 北京: 石油工业出版社, 2002.
[5] 陆德明. 石油化工自动控制设计手册(第二版). 北京: 化学工业出版社, 1993.
[6] 夏清, 陈常贵. 化工原理(下册). 天津: 天津大学出版社, 2005.
[7] 金以惠. 生产过程先进控制. 化工自动化及仪表.
[8] Narciso F.Macia, George J. Thaler. 动态系统建模与控制.北京: 清华大学出版社, 2006.





.jpg)




