- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 磁致伸缩换能器电气模拟中阻抗圆图的应用研究 技术领域 工厂信息化 行业 简介 分析了磁致伸缩换能器的等效电路模型,并且提出了用阻抗圆图确定换能器电气模拟网络的电气元件参数的计算方法。最后通过对试验数据的分析和采用曲线拟合的方法进一步对阻抗圆图的应用进行说明。 内容  李继容(1976—)
李继容(1976—)
女,湖南邵东人,讲师,硕士,研究方向为虚拟仪器、量子通信等。
1 引言
铁磁材料和亚铁磁材料在一定的磁场作用下,长度会发生伸长或缩短的微小变化,这一现象被称作磁致伸缩效应。磁致伸缩的应用相当广泛,涉及到许多先进的民用技术领域和军事技术领域,其中一个主要的应用就是磁致伸缩换能器。磁致伸缩换能器能够把大功率的电能转换为很强的超声波振动,因而可利用所产生的高强度超声波来改变物质的性质和状态,如超声清洗、乳化、钻孔、粉碎、凝聚和超声切割加工等;也可以利用磁致伸缩换能器发射大功率的超声波,用于金属探伤、水下物体探测等。不同的应用领域对磁致伸缩换能器有不同的性能要求。因此,磁致伸缩换能器的谐振频率、机械品质因数和工作带宽等特征参量的确定,对于磁致伸缩换能器的设计及应用有着很重要的意义;同时根据上述特征参量也容易确定换能器的机械耦合系数等其他参量,对换能器新型材料的研究也具有重要的指导意义,如当在磁致伸缩材料中加入少量稀土元素如铽—镉—铁合金,其将具有磁致伸缩性好、杨氏模数小以及磁—机械耦合系数高的特点,采用此类磁致伸缩材料制成的换能器尺寸紧凑同时工作频率明显降低。
2 机电模拟系统
因为换能器的设计者大多数对电网络理论有深入的了解,而对动力学或声学则了解较少,加上大多数有关换能器文献都是以电气方面的术语给出的,因此为了设计和完善新型换能器,设计者通常应用机电模拟理论将换能器的机械系统变成便于分析系统状态的电系统。与建立在换能器数学模型基础上的数值分析方法相比,只要确定了相似的电系统的电路图和参量,就可以充分利用电路及网络理论来分析计算实际的机械系统。与其它的声测法、力测法和光测法相比,由于电系统的电路元件易于更换,测电压电流都比较容易,为模拟和实验提供了更大的方便,故换能器特征参数的确定多采用基于机电模拟系统的电测法。
所谓机电模拟是建立在所研究的机械系统的微分方程和等效电路的微分方程相似的基础上的模拟。机电模拟系统应具有以下性质:(1)具有同形式的微分方程;(2)具有同样的拓扑微分方程;(3)具有同样的标量积的变量。在线性机械系统中,能与电系统参量相对应的模拟方案通常有力—电压模拟和力—电流模拟,各参量的对应关系如表1所示。
表1 力-电压模拟和力-电流模拟系统中参量的对应关系机械系统(力) 力F 速度V 位移X 质量Mm 力阻Rm 柔量Cm 电系统(电压) 电压U 电流I 电荷Q 电感 L 电阻R 电容C 电系统(电流) 电流I 电压U 磁链ψ 电容C 电导G 电感L
3 磁致伸缩换能器的等效电路
由于在电气和机械系统之间没有唯一的模拟,要将磁致伸缩换能器的机械系统变换成等效电路模型就必须选择合适的机电模拟系统。针对磁致伸缩换能器的特点可以选择力等效电流的机电模拟系统。在该模拟系统中,机械跨形变量(速度V)对应于电跨形变量(电压U),机械穿行变量(力F)对应于电穿形变量(电流I),磁致伸缩效应则由机电变量器模拟。图1给出了在该机电模拟系统下磁致伸缩换能器的等效电路。
图1中,Ld为受夹持磁致伸缩换能器(带制动铁芯,即铁芯无机械振动时)激励线圈的电感,Rd表示受夹持磁致伸缩换能器的各种损耗,如线圈的电阻、漏磁损耗、磁滞损耗和涡流损耗等。Mm、Cm、Rm分别为换能器的等效质量、柔量以及机械内耗力阻。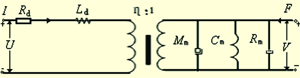
图1 磁致伸缩换能器的等效电路
将机电变量器移到网络的右边就可以得到换能器严格意义上的电气模拟网络如图2所示。
图2 中的电气元件参数C、L、R与图1中的机械元件参数Mm、Cm、Rm的关系为C=Mm/η2、L=Cmη2、R=η2/Rm,其中η为磁电变换系数,它和Mm、Cm及Rm 都决定于磁致伸缩换能器的材料、尺寸和振动模式。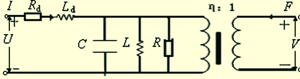
图2 磁致伸缩换能器的电气模拟网络
当换能器机械空载时(即对应于电气开路时),换能器的输入阻抗Z由下面两个部分组成:(1)铁芯无机械振动时换能器的等效输入阻抗或称之为带制动铁芯激励线圈的阻抗Zd=Rd+jwLd;(2)无激励电流时由换能器铁芯机械振动形成的等效输入阻抗Ze,即Z=Zd+Ze其 中
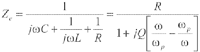 (1 )
(1 )
式中,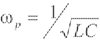 ,为换能器的谐振角频率;
,为换能器的谐振角频率;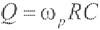 ,是换能器的品质因数[25]。
,是换能器的品质因数[25]。
4 磁致伸缩换能器的阻抗圆图
所谓圆图,实际上是根轨迹的一种。在电路分析中常用图解法来研究电路中的各物理量之间的关系,即确定出代表这些物理量的矢量的终端几何位置。通常这些几何位置称为矢端曲线或轨迹图,如果曲线为圆形,则该矢端曲线称为圆图。
下面用交流电路的复数表示研究等效电路中的无激励电流时由换能器铁芯机械振动形成的等效输入阻抗 Ze ,
令频率微调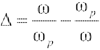 ,则式(1)可改写为
,则式(1)可改写为
Ze=Re+jXe (2)
其中,Re表示动态电导,Xe表示动态电纳,由式(2)可知:
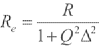 (3)
(3)
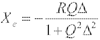 (4)
(4)将式(3)、式(4)两式化简得:
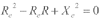
将上式配方即可得方程:
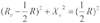 (5)
(5) 显然,当W<Wp,;
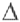 <0当W>Wp时,
<0当W>Wp时,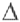 >0。如果用动态电导Re表示横坐标, 动态电纳Xe表示纵坐标。当频率改变时, 式( 5)代表圆心在(0.5R , 0) , 半径为0.5R的一个圆。因此Ze的轨迹是圆图, 且由于
>0。如果用动态电导Re表示横坐标, 动态电纳Xe表示纵坐标。当频率改变时, 式( 5)代表圆心在(0.5R , 0) , 半径为0.5R的一个圆。因此Ze的轨迹是圆图, 且由于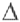 既可以取正值,又可以取负值使得Ze的轨迹是一个完整的圆,如图3 所示。
既可以取正值,又可以取负值使得Ze的轨迹是一个完整的圆,如图3 所示。
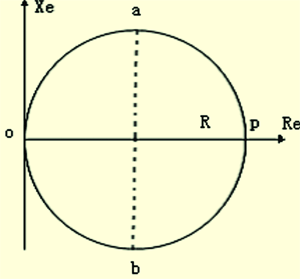
图3 磁致伸缩换能器等效输入阻抗Ze的圆图
图3中的a点(Re=Xe)和b点(Re=-Xe) 的角频率为象限角频率ω1、ω2,p点(Xe=0)的角频率为谐振角频率ωp。将a点、b点、p点的坐标值分别代入式(3)和式(4)可得:
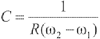 (6)
(6)
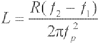 (7)
(7)
如果将 , , (fp、f1、f2分别为磁致伸缩换能器的谐振频率及象限频率)代入式(6)及(7),则有
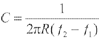 (8)
(8)
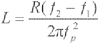 (9)
(9)
5 磁致伸缩换能器的阻抗圆图应用举例
所测得的实验数据见表2,根据实验所测得的数据,对该换能器在3kHz~50kHz范围内机械空载时的输入阻抗Z的实部R和虚部X及其模|Z|的值做输入阻抗特性曲线分析可知,只能确定谐振角频率的大致位置,而不能精确确定它的值。
而理想状态下,Rd 、 Ld均为常数。因此,可以通过该磁致伸缩换能器从3kHz~50kHz频率范围内的输入阻抗Z中分离出Ze,从而由前面分析的Ze的阻抗圆图再确定此换能器的谐振频率fp及其电气模拟参数R 、L、C。
表2 3kHz~50kHz频率段的实验数据
f(kHz) R(Ω) X(Ω) |Z|
3.00 9.1 41.8 42.8
4.00 12.9 54.5 56.0
5.00 16.9 66.1 68.2
6.00 20.4 78.4 81.0
7.00 25.3 88.0 91.6
8.00 29.5 99.5 103.8
9.00 34.5 108.9 114.2
10.00 40.0 120.2 126.7
12.00 52.4 140.6 150.0
14.00 67.3 160.8 174.3
16.00 88.5 182.6 202.9
18.00 144.3 206.1 251.6
20.00 115.5 71.9 136.1
24.00 87.2 192.1 211.0
30.00 121.6 244.1 272.7
35.00 157.0 268.5 311.0
40.00 182.0 291.0 343.2
表3 拟合后的数据
f (kHz) μ1 μ2 3.00 76.3 17.2
4.00 74.7 18.5
5.00 73.1 18.6
6.00 71.6 19.2
7.00 70.1 19.5
8.00 68.6 19.9
9.00 67.2 20.2
10.00 64.5 21.4
12.00 61.2 22.0
14.00 57.3 22.6
16.00 55.1 22.7
18.00 52.9 23.0
20.00 51.0 23.3
24.00 47.9 23.9
30.00 44.8 24.7
35.00 41.7 25.8
40.00 39.5 25.6
45.00 38.1 25.6
50.00 37.6 25.5
在一次线性逼近的近似条件下可以认为,对于远离谐振频率fp的区域3kHz~9kHz和30kHz~50kHz,换能器输入阻抗Z即为带制动铁芯的激励线圈的等效阻抗Zd。但是由于谐振频率fp附近的某个范围内的Zd无法获得,所以希望通过对远离谐振频率段的Zd的分析,获得磁致伸缩换能器在3kHz~50kHz频率范围的 Zd,进而获得Ze。
由铁磁学理论可知,磁致伸缩换能器的相对磁导率 μ=B/( Hμ0 )=μ1 j-μ2 ;μ的实数部分μ1与铁磁材料在交变磁场中的储能密度相关,而虚部μ2则与它在单位时间内损耗的能量有关。当磁致伸缩换能器的激励线圈匝数为n,换能器铁芯长度为l,换能器铁芯截面积为S,激励电流频率为f时,带制动铁芯的换能器输入阻抗Zd为:
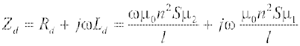 因此:
因此:
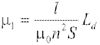
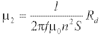
所以希望根据实验数据能确定相对磁导率μ以及与频率的关系μ1( f )和μ2( f )。虽然在3kHz~9kHz和30kHz~50kHz的区间谐振频率两侧的μ1( f )和μ2( f )能够通过实验得到,但10kHz~30kHz频率区间的μ1( f )和μ2( f )无法由实验数据直接获得。然而由磁性材料的物理特性知道,磁性材料的相对磁导率μ中的μ1,μ2在整个频率范围内的变化应该呈现单调、光滑和连续的变化,基于这个假设可以由3kHz~9kHz和30kHz~50kHz的区间的μ1,μ2来确定整个频率范围3kHz~50kHz的μ1,μ2,所以本文通过应用LabVIEW中曲线拟合模块,对由实验数据所获得的数据μ1( f )和μ2( f )进行拟合,从而得到整个频率范围3kHz~50kHz的μ1( f )和μ2( f )。最终拟合后所得方程为:
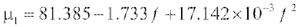
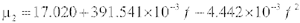
根据拟合方程,就可以计算出拟合后全频范围3kHz~50kHz的u1和u2,拟合结果见表3。因此由μ1和μ2计算出磁致伸缩换能器(带制动铁芯)的阻抗Zd中激励线圈各种损耗Rd和电感抗Xd,进而确定磁致伸缩换能器激励线圈(无激励电流)的阻抗Ze中各种损耗Re 和电感抗Xe。
将计算出的参数Re,Xe和参数作图,可得图4,从而从图中的a点(Re=Xe) 及b点(Re=-Xe) 可以确定f1=18.6 (kHz),f2=20.2(kHz), 进而确定
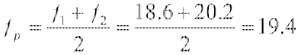 (kHz)
(kHz)因此可以通过fp, f1, f2求出电气参数R 、L 、C。
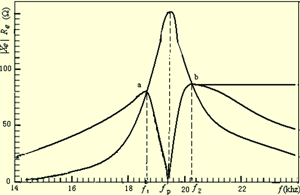
图4 Re( f )和|Xe( f )| 特性曲线图因为R为换能器谐振频率处的电阻Re的值,所以由图4可知R=150.0(Ω) ,由式(8)和式(9)可计算 L、C的值。
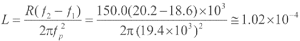 (H)
(H)
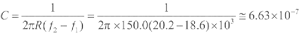 (F)
(F)
6 结束语
磁致伸缩换能器的电气模拟在换能器的设计及研究方面占据重要的地位。本文对磁致伸缩换能器的等效电路输入阻抗特性进行了分析,通过分析磁致伸缩换能器无激励电流时由机械振动形成的换能器的等效输入阻抗Ze 的特性,提出了一种根据 Ze的阻抗圆图确定磁致伸缩换能器的三个重要频率:象限频率f1、 f2及谐振频率fp,进而由此确定磁致伸缩换能器电气模拟网络电气元件参数R、L 、C的计算方法,最后通过曲线拟合的方法对换能器的相关实验数据进行曲线拟合,并对拟合结果进行分析,最终确定了磁致伸缩换能器电气模拟网络参数。本文的测试方法在磁致伸缩换能器的电气模拟领域有所创新,且已在有关磁致伸缩换能器的研究中得到了较好的应用。
参考文献:
[1] 鲍芳,李继容,王春茹.磁致伸缩器件及其应用研究[J].传感器技术,2001,20(8):1-3.
[2] 李继容,何湘初. 一种确定磁致伸缩换能器电气模拟参数的方法[J].传感器技术,2004,23(5):65-67.
[3]廖少彬.铁磁学(下册)[M].科学出版社.1998 :1-100.
[4] National Instruments Corporate.LabVIEW User Manual[M].USA,1998:17.1-17.23.
[5]李继容.一种网络化测试系统及其磁致伸缩器件电器模拟的应用[D].广东工业大学图书馆,2003.6:1-66.





.jpg)




