- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 基于蚁群算法的PID控制器智能优化 技术领域 人机界面 行业 简介 PID控制由于算法简单、鲁棒性好在过程控制中获得了广泛的应用,但是经典的Z-N算法整定的PID参数却并不是最佳的。蚁群算法是一种新型的优化算法,具有收敛速度快、鲁棒性强的优点。本文介绍了蚁群算法的数学模型,针对某个线性系统设计了基于蚁群算法的智能PID控制器,仿真表明智能PID控制器具有良好的控制性能。 内容  孟令雅(1973—)
孟令雅(1973—)
女,河南南阳人,讲师,硕士,研究方向为控制理论与控制工程。
1 引言
PID控制由于其算法简单、鲁棒性好在过程控制中获得了广泛的应用,但是经典的Z-N算法整定的PID参数却不是最佳的,为此需要研究更好的算法来优化PID控制器的参数。目前已经出现一些优化PID控制器参数的方法,如单纯形法、梯度下降法、专家整定法等。虽然这些方法都具有良好的寻优特性,但是却存在着一些弊端,如单纯形法对初值比较敏感,容易陷入局部最优,专家整定法过分依赖专家的经验等等。随着计算机技术和智能控制理论的发展,近几年来,基于仿生优化算法的PID参数优化取得了很多成果[1~4]。
蚁群算法是一种新型的仿生优化算法,采用并行计算机制,具有收敛速度快、鲁棒性强的优点,特别适合求解组合优化问题。本文将蚁群算法和PID控制算法相结合,利用蚁群算法的全局寻优能力来优化PID控制器的三个参数,仿真表明所设计的智能PID控制器具有良好的控制性能。
2 蚁群算法
蚁群算法是意大利学者Dorigo Macro在1991年提出的一种新型的仿生优化算法,它是一种基于种群的启发式搜索算法,充分利用了蚁群能够搜索到从蚁巢到食物源之间最短路径的集体寻优特征来构造最优解,在组合优化问题的求解中获得了广泛的应用,目前对蚁群算法的研究已经由单一的旅行商问题渗透到了多个应用领域,如调度问题、背包问题、车辆路径问题、连续函数优化、故障识别、数据挖掘、图像处理等等。
以最常用的Ant-Cycle模型为例,蚁群算法寻优的过程大致可以分为三个步骤:
(1)状态转移。按照启发式搜索规则,首先根据初始信息素大小和启发信息,按照公式(1)和(2)计算第K只蚂蚁从城市i转移到城市j的概率,蚂蚁选择转移概率大的城市作为转移的目标。
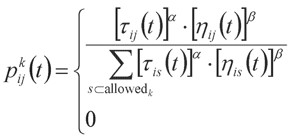 (1)
(1)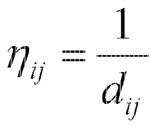 (2)
(2)
其中,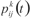 表示第K只蚂蚁从城市i转移到城市j的概率;
表示第K只蚂蚁从城市i转移到城市j的概率;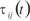 是城市i到城市j之间路径上的信息素;allowedk表示蚂蚁K允许转移的城市集合;dij表示城市i到城市j之间的距离;
是城市i到城市j之间路径上的信息素;allowedk表示蚂蚁K允许转移的城市集合;dij表示城市i到城市j之间的距离;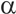 是信息启发式因子,表示轨迹的相对重要性,
是信息启发式因子,表示轨迹的相对重要性,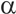 越大,蚂蚁越倾向于选择以前走过的路径;
越大,蚂蚁越倾向于选择以前走过的路径;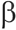 是期望启发式因子,表示能见度的相对重要性,
是期望启发式因子,表示能见度的相对重要性,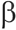 越大,蚂蚁越倾向于选择局部最短路径。
越大,蚂蚁越倾向于选择局部最短路径。
(2)计算最短路径。当每只蚂蚁都遍历了所有城市之后,就完成了一次循环。计算每只蚂蚁在本次循环中走过的路径的总距离,并进行比较,距离最短的路径作为本次循环的最优解。
(3)更新信息素,开始下一次循环。按照公式(3)、(4)和(5)更新路径上的信息素。
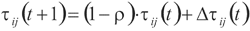 (3)
(3)
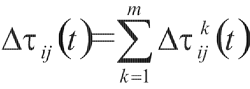 (4)
(4)
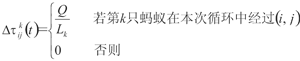 (5)
(5)
其中,Lk是第K只蚂蚁在本次循环中走过的路径的总距离;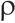 是信息素的挥发系数,0<
是信息素的挥发系数,0<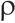 <1 ;Q是信息素强度。可以看出,路径上的信息素一边随时间挥发,一边根据蚂蚁的经验进行累加。而且在上次循环中经过的路径越短,则路径上的信息素增加就越多。而从(1)式可以看到,路径上的信息素越大,该路径被选择的几率就越大,从而形成了一个信息的正反馈效应,最后几乎所有的蚂蚁都选择了最短路径,即蚁群找到问题的最优解。
<1 ;Q是信息素强度。可以看出,路径上的信息素一边随时间挥发,一边根据蚂蚁的经验进行累加。而且在上次循环中经过的路径越短,则路径上的信息素增加就越多。而从(1)式可以看到,路径上的信息素越大,该路径被选择的几率就越大,从而形成了一个信息的正反馈效应,最后几乎所有的蚂蚁都选择了最短路径,即蚁群找到问题的最优解。
蚁群算法的数学模型虽然不是很复杂,但是算法在实现时却不是那么容易。在蚁群算法中,存在着几个非常重要的关联参数: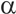 、
、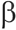 ,
,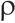 、Q以及蚁群中的蚂蚁个数m,它们都与算法的收敛性和快速性密切相关,在应用时必须正确选择这些参数的组合,才能发挥算法的优势,否则可能导致算法的不收敛。然而遗憾的是,到目前为止,蚁群算法的参数选择还没有统一的理论依据。许多学者对此进行了深入的研究,取得了一些卓有成效的成果。蚁群算法的创始人Dorigo Macro在文献[5]中给出了参数的一般范围,文献[6]对参数选择进行了数字仿真研究,给出了参数
、Q以及蚁群中的蚂蚁个数m,它们都与算法的收敛性和快速性密切相关,在应用时必须正确选择这些参数的组合,才能发挥算法的优势,否则可能导致算法的不收敛。然而遗憾的是,到目前为止,蚁群算法的参数选择还没有统一的理论依据。许多学者对此进行了深入的研究,取得了一些卓有成效的成果。蚁群算法的创始人Dorigo Macro在文献[5]中给出了参数的一般范围,文献[6]对参数选择进行了数字仿真研究,给出了参数 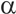 、
、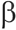 、
、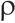 的一般选择方法,文献[7]提出了参数选择“三步走”的原则。根据这些研究成果,结合具体的控制过程,就可以得到蚁群算法中关联参数的一个优化组合。
的一般选择方法,文献[7]提出了参数选择“三步走”的原则。根据这些研究成果,结合具体的控制过程,就可以得到蚁群算法中关联参数的一个优化组合。
3 基于蚁群算法的PID参数优化
以单位负反馈系统为例,基于蚁群算法的智能PID控制系统如图1所示。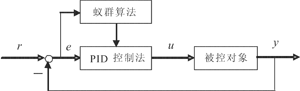
图1 基于蚁群算法的智能PID控制系统为了优化PID参数,首先需要定义蚁群算法寻优的评价函数,通常可以选择衡量控制性能的误差目标函数ISE 、IAE、ITAE等作为评价函数。根据偏差的大小和所定义的评价函数,利用蚁群算法进行全局寻优,就可以得到PID控制器的三个参数。
以工业过程中典型的带有纯滞后的二阶被控对象为例,设被控对象的传递函数为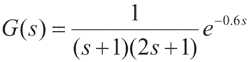 ,选择基本蚁群算法的参数为:
,选择基本蚁群算法的参数为: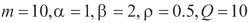 ,性能评价函数为
,性能评价函数为ITAE,即:
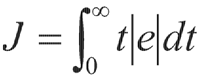 优化后的的PID控制器参数为:
优化后的的PID控制器参数为: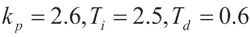 ,闭环单位阶跃响应曲线如图2所示,其中实线表示基于蚁群算法优化的PID控制曲线,虚线表示基于Z-N法整定的PID控制曲线。
,闭环单位阶跃响应曲线如图2所示,其中实线表示基于蚁群算法优化的PID控制曲线,虚线表示基于Z-N法整定的PID控制曲线。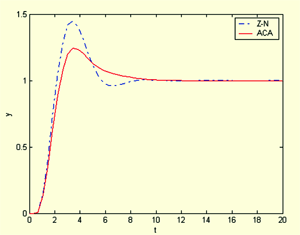
图2 基于ACA和Z-N设计的单位阶跃响应曲线从单位阶跃响应曲线可以看出,基于ACA设计的智能PID控制器的控制性能明显优于基于Z-N法整定的控制器的控制性能。
4 结论
论文将蚁群算法和PID算法相结合,设计了智能PID控制系统,利用蚁群算法的全局寻优能力,优化PID控制器的三个参数,仿真表明优化后的PID智能控制器具有较好的控制性能。在蚁群算法的参数选择上还需要进一步的研究,以加快算法的收敛性能,从而能够有效地实现在线优化和实时控制的目标。
参考文献
[1] 李奇等. 一类神经网络智能PID控制算法的分析与改进[J]. 控制与决策. 1998,13(4):311~316.
[2] 南海鹏等. 基于遗传算法的水轮机智能PID调速器研究[J].水力发电学报. 2004,23(1)107~112.
[3] 彭道刚等. 模糊免疫PID控制在主汽温控制系统中的应用[J]. 计算机测量与控制. 2005,13(3):250~251.
[4] 段海滨等. 基于蚁群算法的PID参数优化[J]. 武汉大学学报(工学版). 2004,37(5):97~100.
[5] Dorigo M, Colorni A. Ant system: optimization by a colony of cooperating angents[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B. 1996, 26(1):29~41.
[6] 詹士昌等. 蚁群算法中有关算法参数的最优选择[J]. 科技通报. 2003,19(5):381~386.
[7] 段海滨. 蚁群算法原理及其应用[M],北京:科学出版社,2005. 112~116.





.jpg)




