- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 基于PCA和RBF网络的减速箱运行状态诊断技术 技术领域 工业以太网 行业 简介 内容
Abstract: As to the complicated nonlinear relation existing between running status of gear reducer and characteristic parameters, PCA-based RBF neural network reducer running status diagnostics is put forward. High-dimensional correlated characteristic parameters are transformed into low-dimensional independent characteristic parameters, a RBF neural network classifier is built hereto and the network is used to identify a turbine reducer running status. Theory analysis and Experiment result indicate that PCA and RBF neural network based reducer running status diagnostics has advantages of simple model and quick detecting speed, and can play effective role in practical application. 杨帆(1973—)
杨帆(1973—)
男,陕西礼泉人,讲师,硕士,主要研究领域为智能信息处理技术、计算机监控技术。
基金项目:陕西科技大学自然科学基金资助(ZX05-37);陕西省工业攻关项目(2006K05-G18)
摘要:针对减速箱运行状态和特征参数之间存在的复杂非线性关系,提出了基于主成分分析的RBF神经网络减速箱运行状态诊断方法。该方法用主成分分析方法将高维相关特征参数转化为低维相互独立的特征参数,在此基础上建立了RBF网络分类器,并用该网络对某汽轮机减速箱的运行状态进行识别。理论分析和实验结果表明,基于PCA和RBF网络方法的减速箱运行状态诊断技术具有模型简单,检测速度快等优点,可以在实际应用中发挥有效作用。
关键词:主成分分析;RBF网络;特征提取;状态诊断
Key Words: PCA;RBF network;Characteristics extraction;Status Diagnosis
减速箱是各类机械传动部分的关键部件。根据研究和统计分析表明,减速箱内各零件失效比最大,约占机械传动系统故障的 60%。因此进行状态监测和故障诊断,识别设备的工作状态,及时发现异常情况,对故障进行早期诊断和预报,从而有针对性、有计划性地采取检修措施,确保设备安全运行就显得非常重要。
在机械故障诊断中一般描述系统采用的参数越多,被认为对系统的认识越深刻。但是如果利用过多的系统参数作为诊断识别系统的数据,一方面由于参数之间不可避免的相关性以及量测过程中噪声的引入,就会使得常用的诊断算法性能下降;另外一方面,引入的参数越多,就会占用大量的机器处理时间和存贮空间,影响诊断的速度。所以在诊断过程中提取核心特征参数、抑制噪声数据是简化计算过程,提高诊断识别率的重要步骤。本文采用了主成分分析( PCA) 方法进行特征再提取,通过创建一个替换的、较小的变量集来“组合”原始特征的精华,原始数据可以投影到该较小的集合中。在PCA特征提取的基础上,用RBF神经网络分类器进行了某汽轮机减速箱的运行状态诊断,取得了较好的诊断结果。
1 PCA方法基本原理
成分分析是用来在数据中寻找恰当的特征表示的方法。主成分分析(principle component analysis)PCA一般用来对输入样本集进行预处理,可把多个存在复杂非线性关系的特征参数转化为较少的彼此不相关的综合变量,接着以这些较少的向量形成新的网络输入变量,从而降低神经网络输入的变量数,优化网络结构。PCA的对象是过程变量的样本数据矩阵。数据矩阵的行表示采样值或观察值,列表示变量。PCA产生一个压缩的统计模型——主元模型,模型给出了变量的线性组合,描述了数据变化的主要趋势。主元模型使原标准差的平方重新分布,大多数标准差平方会分布在第一主元上,其次分布在第二主元上,依此类推。按某种准则将最后几个主元视为分解残差予以忽略,则有可能利用最少主元来说明最多的信息。主元模型舍弃了部分残差而保留体现数据变异的主要方向,从而达到抽取系统信息,清除系统干扰的目的。
实际应用中,合理确定主元个数进而建立主元模型非常重要。通常采用方差累积贡献率百分比(CPV)原则,选择百分比大于85%的主元个数。在基于PCA的过程状态、故障的诊断中,一般用来描述正常运行过程的主元不超过3个(Kresta等,1991)。主成分分析的主要计算步骤如下:
(1) 原始样本标准化
为了消除量纲和数量级不同的影响,采用均值标准差标准化方法处理原始样本数据。
(2) 建立标准化变量的协方差矩阵,求解矩阵的特征值和特征向量
利用标准化值计算变量之间的相关系数,有k个特征参数可建立k阶相关矩阵。由此矩阵可获得由大到小排列的特征值Ai(i=1,2,L,k),k个特征值对应k个特征向量,每一特征向量包含k个分量。
(3) 根据要求的累计贡献率, 选取主成分
计算第i个主成分对总方差的贡献率,即方差贡献率: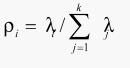 。通常取累计方差贡献率大于85% 所需的主成分,能够代表k 个原始变量所能提供的绝大部分信息。
。通常取累计方差贡献率大于85% 所需的主成分,能够代表k 个原始变量所能提供的绝大部分信息。
(4) 建立主成分方程、计算各主成分值
各主成分值方程为: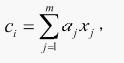 ,其中aj为对应于j 的特征向量的分量, xj为各变量的标准化数值。计算出所需要的各主成分值, 形成新的训练样本集和测试样本集。
,其中aj为对应于j 的特征向量的分量, xj为各变量的标准化数值。计算出所需要的各主成分值, 形成新的训练样本集和测试样本集。
2 基于PCA的RBF网络诊断方法
2.1 RBF神经网络结构
神经网络对复杂问题具有自适应和自学习能力,为解决复杂系统的信息处理和控制等问题提供了新的思想和方法。作为一种前馈型神经网络,RBF网络避免了BP神经网络的冗长繁琐计算,学习速度较通常的BP方法快的多,具有良好的泛化能力,能以任意精度逼近非线性函数。RBF神经网络一般组成结构如图1所示:
RBF网络结构中,输入层由信号源节点组成,传递信号到隐层;输出层一般是简单的线性函数,对输入模式作出响应。隐层节点的变换函数(基函数)是对中心点径向对称且衰减的非负非线性函数,对输入信号将在局部产生响应,也就是说,当输入信号靠近基函数的中央范围时,隐层节点将产生较大的输出,由此看出这种网络具有局部逼近能力,所以径向基函数网络也成为局部感知场网络。作为基函数的形式,最常用的一般是高斯函数: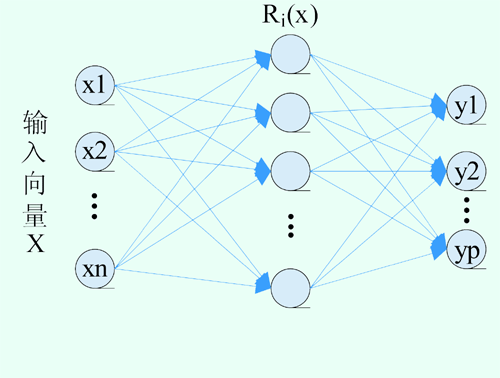
图1 RBF神经网络结构图
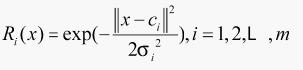
其中x是n维输入向量;Ci是第i个基函数的中心,与x具有相同维数的向量,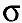 i是i个感知的变量,决定该基函数围绕中心点的宽度;m是感知单元的个数;
i是i个感知的变量,决定该基函数围绕中心点的宽度;m是感知单元的个数;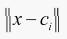 是向X-Ci量的范数,表示两个向量之间的距离,Ri(x)在ci处有唯一的最大值,随着
是向X-Ci量的范数,表示两个向量之间的距离,Ri(x)在ci处有唯一的最大值,随着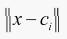 的增大,Ri(x)迅速衰减到0。对于给定的输入
的增大,Ri(x)迅速衰减到0。对于给定的输入 ,只有一小部分靠近x的中心被激活。
,只有一小部分靠近x的中心被激活。
从RBF网络结构可以看出,输入层实现从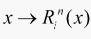 的非线性映射,输出层实现
的非线性映射,输出层实现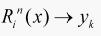 的线性映射,即:
的线性映射,即: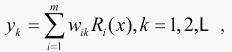 ,其中是输出节点的个数。
,其中是输出节点的个数。
RBF 神经网络的学习过程主要分为两个阶段。首先,根据输入样本求出各隐层节点高斯核函数的中心ci和每个中心的半径Ri。隐层参数确定以后, 还需要求出隐层和输出层之间的权值wik。
2.2 基于PCA的RBF网络诊断模型
基于PCA和RBF神经网络的减速箱运行状态诊断系统实现框图如图2所示。
如前所述,基于PCA的RBF诊断就是利用PCA的方法进行原始数据的预处理,从而获取系统描述主成分,然后利用主成分构造出诊断算法需要的训练数据集,再基于RBF神经网络进行学习和训练。对于采集到的未知状态的运行数据,首先将其变换到主成分空间,然后利用训练好的RBF网络进行运行状态的诊断和识别。其具体处理步骤如下: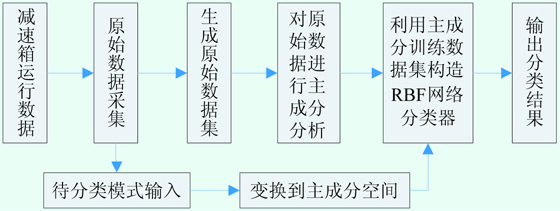
图2 基于PCA和RBF神经网络的减速箱运行状态诊断系统实现框图
(1)获取描述某汽轮机减速箱运行特征参数以及运行状态分类决策结果,形成原始数据集。
(2)基于PCA方法抽取训练数据集的主成分;
(3)构造基于主成分的训练数据集;
(4)基于主成分训练数据集构造并训练RBF神经网络模式分类器;
(5)将新的观测向量(与原始数据维数相同)变换到主成分空间,得到主成分空间的观测对象变量。
在主成分的训练数据集上基于训练好的RBF神经网络进行推理分类。
3 实验过程以及结果分析
为了验证本文提出方法的正确性和有效性,选取一组实际采集的某汽轮机减速箱运行实验数据(表1) 进行运算验证。
表1 汽轮机减速箱运行状态特征数据:
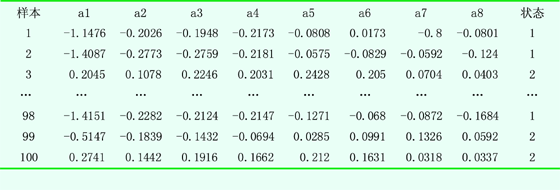
表1中共有100组实测减速箱运行数据,a1~a8为采集到的8个特征参数,表中状态值1表示正常,2表示故障。将样本数据分为2组,选前80个数据进行训练网络,后20个数据进行检验。为了消除由于数据量纲对于最后判决带来的误差,首先进行归一化处理,然后进行主成分分析,计算得到主成分的方差累计贡献率为:76.2117、86.0981、93.3289、98.1578、 99.3166、99.8645、99.9573、100.0000,按照方差累计贡献率>90%获取主成分,最终生成3个主成分x1,x2,x3,其计算方法如下所示。
u1=(-0.3986 -0.3657 -0.3570 -0.3944 -0.3307 -0.3760 -0.2335 -0.3452)’;
u2=(0.0189 -0.3638 -0.3765 -0.07312 -0.0469 0.0691 0.8024 0.2633 )’;
u3=(-0.1959 0.2471 0.3770 0.1793 0.0052 -0.4213 0.5197 -0.5279)’;
使U=(u1 u2 u3)’,与标准化处理后得到的数据集X按照式计算,即可得到原始数据的主要成分表示,如表2所示。
表2 主成分训练数据集: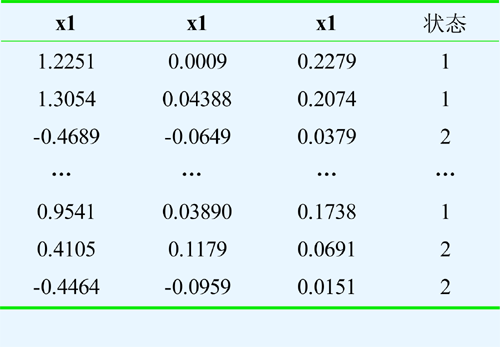
利用主成分训练数据集的前80个数据进行RBF网络的构造和训练,后20个作为测试数据,试验结果表明:基于PCA和RBF神经网络的减速箱运行状态诊断方法的诊断结果与实际完全一致。可见,基于PCA方法将观测向量投影到低维空间,构造出相互独立的主成分观测向量后,可以简化RBF神经网络的结构和计算,对于提高诊断速度的目标作用十分明显。
4 结束语
在减速器状态监测和故障诊断中,将主成分分析与RBF神经网络技术相结合,通过对原始特征参数的降维处理,得到互不相关低维主成分空间特征参数,以此为RBF神经网络的输入向量,进行网络的构造和训练,最后利用训练好的网络进行减速箱的运行状态诊断。相比传统的单纯神经网络状态诊断方法,本文提出的诊断方法由于PCA技术的引入,减少了输入向量的维度,消除了相关信息和噪声数据的影响,简化了神经网络的结构,提高了分析运算的速度,可以在减速箱运行状态的实时诊断中发挥有效作用。其它作者:
张玉杰(1967-),男,陕西武功人,副教授,硕士,主要从事嵌入式智能系统研究;
张彩丽(1973-),女,陕西合阳人,硕士,主要从事机电系统故障诊断技术研究。参考文献
[1]范金城. 数据分析[M]. 北京:科学出版社,2002 141~153.
[2]梁循. 数据挖掘算法与应用[M]. 北京:北京大学出版社,2006 184~187.
[3]任若恩. 多元统计数据分析[M]. 北京:国防工业出版社,1997 92~109.
[4]熊和金. 智能信息处理[M]. 北京:国防工业出版社,2006 123~135.
[5]殷勤业. 模式识别与神经网络[M]. 北京:机械工业出版社,1992 98~104.
[6]曹龙汉. 柴油机智能化故障诊断技术[M]. 北京:国防工业出版社,2005 131~135.
[7] Luo, Rongfu; Misra, Manish; Himmelblau, David M. Sensor fault detection via multiscale analysis and dynamic PCA Industrial and Engineering Chemistry Research, v 38, n 4, Apr, 1999, p 1489-1495.
[8] Abdel-Qader, Ikhlas, PCA-Based algorithm for unsupervised bridge crack detection,Advances in Engineering Software, v 37, n 12, December, 2006, p 771-778.





.jpg)




