控制网

    唐俊奇  (1967－)
男，福建莆田人，副教授/高级工程师，工学学士，(湄洲湾职业技术学院，福建  莆田  351254)研究方向为计算机系统结构、计算机网络。

摘要：单处理机系统难于满足大型数字图像的实时处理要求，多处理机并行工作系统可以提高数字图像处理的效率和效果。本文分析多处理机系统在数字图像处理中的并行化机会，运用数字图像处理中傅里叶变换的特点，在多处理机中实现流水线算法、FFT算法的并行化(二元交换算法)、快速傅里叶变换、基本的主从实现等算法，解决了傅里叶变换和快速傅里叶变换中N取较大值时所产生的顺序复杂性，进而使多处理机系统中能够使多个处理机之间能够更加协调工作，更加有效地利用CPU。

关键词：多处理机；傅里叶变换；并行算法

Abstract: It’s difficult for single processor to satisfy real time processing requirements of large digital image and multiprocessor parallel operation system can enhance the efficiency and result of digital image processing. This paper analyses the parallel opportunity of the multiprocessor system in digital image processing, uses the characteristics of the Fourier Transform in the digital image processing, fulfils the pipeline algorithm, FFT algorithm parallel (dual exchange algorithm) fast Fourier transform, basic master/slave realization and other algorithms in the multiprocessor, settles the sequence complexity when n selects higher value in Fourier transform and FFT, by which a number of processors can work together better in a multiprocessor system and make better use of CPU.

Key words: Multiprocessor; Fourier transform; Parallel algorithm

    图像的增强、恢复和压缩主要手段是傅里叶变换和快速傅里叶变换。多年来，人们一直在单处理机的计算机环境下进行数字图像处理和科学试验。由于单处理机的计算机系统的处理速度、效率和效果不尽人意，因此人们渴望着有更高性能和更高计算速度的计算机出现。多处理机系统正可以满足这方面的要求[1，2，3]。

    在数字图像处理中常常要用经过适当的数学处理后不带比例因子的离散傅里叶变换的显示方式表示[1]，即

   
    
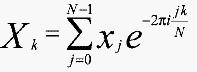
    在该式中求和计算比较容易，特别是如果指数项的值存放在查找表中时，对于N点（如方程式所列出的那样）仍需N2次乘法和加法，即其顺序复杂性为O（N2）。一般情况下人们很难接受这种顺序复杂性(特别是N取较大值时)[2]，需要研究一个合理的算法，以适应科学和生产的需要。本文分析多处理机系统在数字图像处理中的并行化机会，阐述了多个处理机在数字图像处理中的傅里叶变换和快速傅里叶变换并行化算法，它对克服N取较大值时所产生的顺序复杂性并解决如何使多个处理机间并行协调工作，寻找合适的并行算法（傅里叶变换时）以提高整个系统的性能具有极其重要的现实意义。

1　图像处理中傅里叶变换并行化的可行性

    在图像处理中，输入的形式是离散二级函数的一组像素。使用j和k坐标，在（j,k）坐标中像素是x(j,k)。假定该图像是一个方阵，即N＝M，这样二维的傅里叶变换可表示为：

   

    式中的内部累加和是作用于一行中N个点上的一维DFT操作，它将生成一个经变换的行；而外部累加和是作用于一列中N个点上的一维DFT作用。可写成：

   

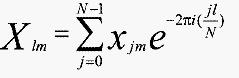
    因此，二维的DFT能被分为两个顺序阶段，一个阶段作用于行元素而另一阶段作用于（已经过变换）列元素。因此需要实现的仅是一维DFT算法[4]。很显然，此过程也可从列开始，然后再是行。具体选择则依赖于为实现有效并行原始数据是如何存放的。由于行变换相互独立，且列变换也相互独立，因而存在有很多的并行化机会，这样也为使用多处理机提供优越性。

2　傅里叶变换在多处理机数字图像处理中的优越性

    在频率域内，图像处理和分析的应用非常广泛。DFT的一个应用领域之一是频率滤波，在平滑和边缘中都要用到它（低通和高通滤波器）。频率滤波早期采用加权掩码，它可用卷积操作描述[3]：
　　  
    h(j,k)=g(j,k)*f(j,k)

    与对称掩码的互相关函数的操作相同，式中g(j,k)描述加权掩码（滤波器），而f(j,k)描述图像。可以证明函数积的傅里叶变换可由各函数变换的卷积确定。

    因此，两个的卷积可将每个函数先进行傅里叶变换，然后将两个变换相乘得到
  
    H(j,k)=G(j,k) ×F(j,k)

    式中F(j,k)是f(j,k)的傅里叶变换，则G(j,k)是g(j,k)的傅里叶变换。此后对其取反变换，就可使结果回到原来的空间域。这种滤波方法比起在空间域中使用简单的加权掩码方法需要更多的计算量，但它可完成其他更复杂的操作。也可对两个完整图像进行卷积以产生一个新的图像。重要的是，由于两者的变换是相互独立的，因此它们可并行地完成，同样也为使用多处理机提供可能性。

3 离散傅里叶变换算法的并行化

    基本的DFT算法以及它的并行化方法可以从以下公式[1]开始：

   

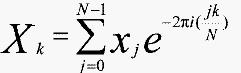
    在使用记号w=e-2πi/N后，可得:

   

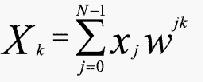
    式中w为旋动系数(twiddle factor)。每个输入值必须乘以旋动系数。用w -1替代w就可得到反变换。

    3.1　顺序代码——单处理机使用的代码
 
    产生全部N点的DFT的顺序代码形式可为：

  for (k =0 ; k < N; k++) {      /* for every point */
   x [k] =0;
   for (j =0 ; j<N; j++)
     x[k] =x[k] +wj*k* x[j];     /* compute summation */
  }

    其中X[k]为第k个被变换点，x[k]为第k个输入，共有N个输入点，而w=e-2πi/N。求累加和的计算要进行复数运算。由于每步求累加和要使用前一点的w的升幂值并乘以wk（即w(j-1)*k*wk=wj*k），因此，上述代码可重写成：

　　for (k =0 ; k < N; k++) {
  x [k] =0;
  　a=1;
   for (j =0 ; j<N; j++)｛
     x[k] =x[k] +a * x[j]; 
     a=a*wk;
  }
　 }
　
    其中a为临时变量。

    3.2　并行代码的实现——多处理机中使用的代码

    在多处理机系统中，可以采用几种方法使上述代码并行化。这里将只简单涉及最明显的主从方法、较明显的流水线方法以及在最后叙述的矩阵－向量乘积方法。

    3.2.1 基本的主从实现

    在主从方法中，N个从进程中的每一个可被指定来产生一个变换值，即第k个从进程生成x[k]。所需的a值可由主进程预先求得，如图1所示。也可使每个从进程同时计算它们各自的值，该方法要求每个从进程拥有一份所在输入点的拷贝，从而会使存储需要增加到N倍。并行求解的时间复杂性为O（N），相对于顺序算法实现的O（N2），该并行方法有了很大的优化。但是，数据点数很可能远大于可用的进程数。此时，每个从进程将需要进行多次累加和。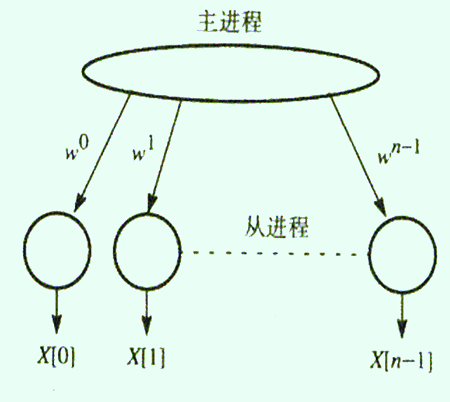

图1  直接实现DFT的主从方法

    3.2.2 流水线实现 

    该算法可采用流水线结构加以实现，因为内层循环中的每次迭代需要使用前一次迭代生成的值。将X[h]的内层循环展开可得：

 x[k]=0;
 a=1;
 x[k]=x[k]+a*x[0];
 a=a*wk；
 x[k]=x[k]+a*x[1]
 a=a*wk；
　　x[k]=x[k]+a*x[2]
　　a=a*wk;
　　x[k]=x[k]+a*x[3]
  ????
　
    其中的每一对语句

 x[k]=x[k]+a*x[0]
 a=a*wk;

    可由一个分离的流水线级完成。

    因为w0＝1，w项的某些可以归约掉。

4　快速傅里叶变换

    快速傅里叶变换（Fast Fourier Transform,FFT）是获取离散傅里叶变换的快速算法，它可使时间复杂性从O（N2）降为O（NlogN）。在下面的论述中，我们假定N是2的次方。

    笔者从具有比例因子的离散傅里叶变换方程开始进行讨论，以表明比例因子不会影响算法的推导：

   

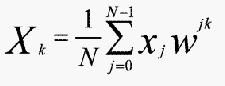
    式中w=e-2πi/N。下面我们描述的一个公式是将求和分解成下两部分来进行的：

   

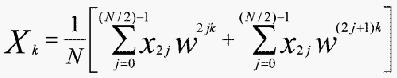
    其中第一项求和处理具有偶下标的x值，而第二项求和处理具有奇下标的x值。重写后可得：

   

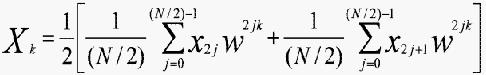
    或是

   

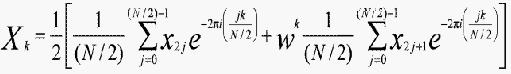
    现在可将每个和看成是一个N/2离散傅里叶变换分别作用于N/2偶数点和N/2奇数点。因此有：

     

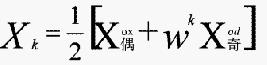
    其中k=0，1，…，N－1，X偶是具有偶下标数x0，x2，x4，…的N/2点的DFT，而X奇则是具有奇下标数x1，x3，x5，…的N/2点的DFT。
 
    现在，若假设k限制为0，1，…，N/2-1，即全部N个值的前N/2个值。这样整个序列可分成为两部分：

    
   

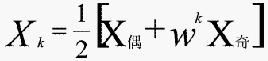
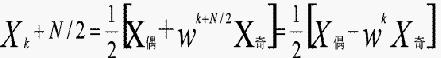
    因为wk+n/2=-wk，其中0≤k≤N/2。这样我们可用两个N/2个点变换来计算xk和xk+N/2。
 
    以上每一个N/2个点的DFT又可分解成两个N/4个点的DFT，此分解可一直进行下去直到对单点进行变换。一个单点的DFT即是该点的值。对每个要变换的点都要进行上述的计算。应注意到，根据X偶和X奇中所使用的数的个数以及指定的X变换的输出下标，在不同级上出现的不同值。注意到由于数的个数以2倍系数减少，相应地w的幂以2倍系数增加，从而方便了旋动系数的获得。（w=e2kπi/(N/2)，e2kπi/(N/4)=w2，e2kπi/(N/8)=w4等）。为清晰起见，1/2比例因子也已被省略，从而在原来的DFT方程中若没有比例因子，则它就不会存在。

    4.1　顺序代码的实现方法

    顺序计算的时间复杂性基本上是O（logN），因为共有logN步，而每一步需要进行正比于N的计算，这里的N是指共有N个数。该算法可用递归或迭代方法加以实现。

    4.2　FFT算法的并行化(二元交换算法)

    由于FFT的顺序计算的时间复杂性为O（NlogN），因而当使用N个处理器时，理想的成本优化并行计算时间复杂性为O(logN)。下面阐述并行化的方法：在图2中，假定为每个数据点（对第j个进程为x[j]，相应于图2中的一行）分配一个处理器。每个进程最终将生成一个变换点。图2中的连接模式称为蝶形连接，如果每一行分配一个处理器，则它可很好地映射到超立方体上，这是因为本级产生的结果将传送给下一级的进程，而该进程所拥有的地址仅与本级的地址有一位不相同。例如，在第一个通信步中，处理0将与处理器8通信，而在下一步中与处理器4通信，再一下步与处理器2通信，最后一步与处理器0通信。

    同样地，如果处理器数小于数据点数，每个处理器将分配有一组数据点，但此时的处理器间通信模式仍具有相同特征。假定有p个处理器和N个数据点，则每个处理器有N/p行。如果N和p均为2的乘方，则下面处理器的编号取数据点下标中logp高位，余下的位则用来标识组内的数据点。图3中显示了N/p=4的情况。

    4.3   分析

    （1）计算 给定p个处理器和N个数据点，每个处理器在每一步将计算N/p个点，而每一个点的计算需进行一次乘法和一次加法。因共需logN步，故并行计算的时间复杂性由下式确定：

　　  tcomm=O(NlogN)

图 3   将处理器映射到16点FFT计算

    （2）通信  若p=N，则每一步都需通信，因而在logN步中的每一步在处理器对之间要进行一次数据交换。假定所使用的是超立方体或其他允许进行同时交换的互连网络，则此时的通信时间复杂性由下式给定：

　　   tcomm=O(logN)

    如果p<N，处理器间通信仅出现在前logp步中。在第一步中，所有p个处理器进行交换；在下一步时，仅有一半处理器进行数据交换；在再下一步时，仅有1/4处理器进行交换，以此类推。如果互连网络允许同时进行交换，则通信时间复杂性可简化成由下式确定：

tcomm=O(logP)

    当然，如果互连网络只允许进行顺序通信，则上述的这些复杂性将变糟。

5　结束语

    充分运用数字图像处理中傅里叶变换和快速傅里叶变换的特点在多处理机中巧妙地实现流水线算法、FFT算法的并行化(二元交换算法)、快速傅里叶变换、基本的主从实现等算法，解决了傅里叶变换和快速傅里叶变换中N取较大值时所产生的那种令人难于接受的顺序复杂性；进而使多处理机系统中多个处理机之间能够更加协调工作，更加有效地利用CPU，为工作提供了方便，达到了预期效果。

参考文献：

    [1] 陈国良.并行算法的设计与分析[M].北京：高等教育出版社，2002.

    [2] [美]Rafael C.Gonzalez，Richard E.Woods等著，阮秋琦，阮宇智等译，数字图像处理[M].北京：电子工业出版社，2003.

    [3] 陈智勇. 计算机系统结构[M].西安：西安电子科技大学出版社，2004.

    [4] WAH B.W., G-J.LI,AND C.F.Yu (1985), ”Multiprocessing of Combinational Search Problems,” Computer,Vol.18,NO 6,pp.93-108.

    [5] 尚明生.相关任务图的一种有效并行调度算法[J].计算机工程,2005,31(14),18-21.