当前位置:首页»企业
- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 一类混沌系统的分数阶广义同步 技术领域 电源 行业 电子制造 简介 针对一类参数未知的混沌系统,基于分数阶微积分和Lyapunov稳定性理论,设计出了一族分数阶广义同步控制器,此族控制器可通过选择不同分数阶次得到不同的控制效果,并且都能保证闭环混沌系统达到渐近广义同步. 数值试验验证了此方法的有效性。 内容 
张隆阁 (1979 -)
男,硕士,讲师,研究方向为分数阶微积分在控制中的应用。
基金项目:华北电力大学青年基金(200611001)
摘要:针对一类参数未知的混沌系统,基于分数阶微积分和Lyapunov稳定性理论,设计出了一族分数阶广义同步控制器,此族控制器可通过选择不同分数阶次得到不同的控制效果,并且都能保证闭环混沌系统达到渐近广义同步. 数值试验验证了此方法的有效性。
关键词:广义混沌同步;分数阶微积分;Lyapunov稳定性
Abstract: Based on fractional calculus and Lyapunov stability theory, a sort of
fractional generalized synchronization is designed for a class of chaostic systems.
Different control effect and the stability of the closed chaotic system can be obtained
by selecting different fractional order. Numerical simulations show the effectiveness of
the method.
Key words: Generalized chaotic synchronization; fractional calculus; Lyapunov stability
1 引言
混沌现象是自然界中广泛存在的一种非线性现象,混沌系统对初值极其敏感,从而导致了其类随机特性。自从L.M. Pecora和T.L.Larrol于1990年提出混沌系统的驱动-响应同步方法以来 [1] ,由于混沌同步在通信保密和震荡发生器的设计等方面的成功应用,越来越多的受到学者们的重视,成为混沌和控制领域的研究热点 [2-5] ,常用的有反馈同步、自适应同步、脉冲同步、耦合互同步等方法。另一方面,分数阶微积分已较好的应用于控制和信号处理等领域中 [6-7] 。本文基于Lyapunov稳定性理论,设计出了分数阶广义同步控制器,并以chen系统的分数阶广义同步为例,验证了此方法的有效性。
2 分数阶微积分的定义
分数阶微积分有多种定义方式 [8] 。Caputo定义有传统的易于物理上解释和实现的初始条件,并且对常数的分数阶微分为0。所以在控制问题研究中应用较多的是Caputo定义。本文采用Caputo定义。
定义1分数阶积分:一元函数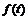 的
的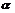 阶积分定义为[8]:
阶积分定义为[8]:
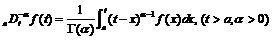 (1)
(1)
其中,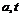 分别为积分的下界和上界,
分别为积分的下界和上界,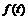 为被积函数,
为被积函数,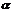 为积分次数,
为积分次数,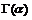 为欧拉伽马函数。
为欧拉伽马函数。
定义2分数阶微分:一元函数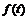 的
的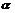 阶维微分定义为 [8]:
阶维微分定义为 [8]:
 (2)
(2)
其中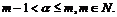 。
。
3 问题描述及同步控制器的设计
考察两个动力学系统
 (3)
(3)
 (4)
(4)
(3)为驱动系统,(4)为响应系统。其中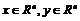 分别为两系统的状态向量。
分别为两系统的状态向量。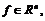 ,
,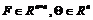 ,为未知的参数向量,
,为未知的参数向量, 为未知参数向量
为未知参数向量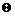 的估计值,
的估计值,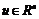 为广义同步控制器。设
为广义同步控制器。设 为一常数,当
为一常数,当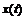 和
和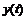 满足
满足
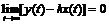 (5)
(5)
时,称系统(3)和(4)广义同步。令 ,将(3)和(4)代入(6),可得
,将(3)和(4)代入(6),可得
 (6)
(6)
假设未知参数 是分数阶的时变量,并且假设有最简单的分数阶模型
是分数阶的时变量,并且假设有最简单的分数阶模型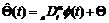 。构造积分型Lyapunov函数
。构造积分型Lyapunov函数 ,对Lyapunov函数求导,则有
,对Lyapunov函数求导,则有
 (7)
(7)
将(6)式代入(7)式,且取广义同步控制器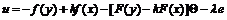 和参数自适应率
和参数自适应率 时,
时,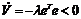 ,由推广的分数阶Lyapunov理论[9] 知,所得闭环系统是稳定的。
,由推广的分数阶Lyapunov理论[9] 知,所得闭环系统是稳定的。
4 chen系统的广义同步
Chen混沌系统的模型
 (8)
(8)
其中,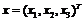 是系统的状态向量,而
是系统的状态向量,而 是待估计的未知常数。当
是待估计的未知常数。当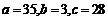 时,系统(8)产生混沌现象,存在混沌吸引子。将(8)式化为(3)式的形式
时,系统(8)产生混沌现象,存在混沌吸引子。将(8)式化为(3)式的形式
 (9)
(9)
其中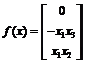 ,
,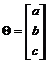 ,
,
 ,
,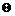 为未知参数,式(9)为驱动系统。响应系统可以表示为
为未知参数,式(9)为驱动系统。响应系统可以表示为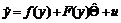 ,其中
,其中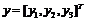 是系统的状态向量,
是系统的状态向量, ,
,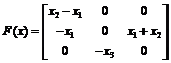 ,
,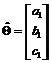 为
为 的估计值,
的估计值,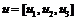 为广义控制器。由上一小节讨论可知,当参数自适应律和控制律分别为
为广义控制器。由上一小节讨论可知,当参数自适应律和控制律分别为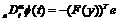 和
和 时,能实现系统的广义同步。此时有
时,能实现系统的广义同步。此时有
 和
和
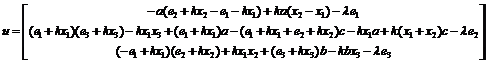
在仿真中,取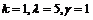 ,参数
,参数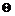 的估计初始值为
的估计初始值为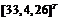 ,分数阶次为0.95时,可使主从系统实现同步,其仿真结果见图1。
,分数阶次为0.95时,可使主从系统实现同步,其仿真结果见图1。
5 结论
本文研究了一类参数不确定的混沌系统的分数阶广义同步。基于分数阶的Lyapunov稳定性理论,证明了此种方法设计出的同步控制器是全局稳定的,并且可以根据未知参数分数阶次的选择,得到不同的控制效果。最后以chen系统为例验证了此方法的有效性。
(a) generalized synchronization errors of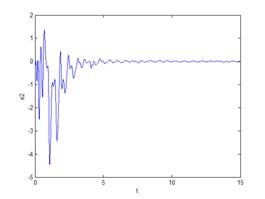
(b) generalized synchronization errors of
(c) generalized synchronization errors of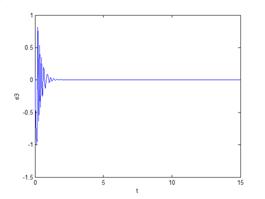
图1 广义同步误差曲线
参考文献
[1] Pecora L M,Carroll T L.Synchronization in chaotic systems[J]. Phys. Rev. Lett.,1990,64(8):821~824.
[2] Chen G,Dong X. From chaos to order: Methodologies, Perspectives and Applications[M]. Singapore: World Scientific,1998.
[3] Agiza H N,Yassen M T. Synchronization of R sssler and Chen chaotic dynamical
systems using active control[J]. Phys.Lett.A,2001,278(4): 191~197.
[4] Batajas-Ramrez J G,Chen G,Shieh L S. Hybrid chaos synchronization[J]. Int. J. of Bifurcation and Chaos,2003,13(5):1197~1216.
[5] Xiao Jiang-wen,Yu Yi. Coupled adaptive synchronization for Chen chaotic
systems with different. parameters[J]. Chaos,Solitons and Fractals,2007,33(3): 908~913.
[6] Podlubny I.Fractional-order systems and PI -controllers. IEEE Transactions on
Automatic Control[J]. 1999,44(1),208-214.
[7] Vinager B M, Petrá? Iand Podlubny I. Using fractional order adjustment rules and
fractional order reference models in model-reference adaptive control[J]. Nonlinear
Dynamics 2002,29:269-279.
[8] Podlubny I .Fractional Differential Equations[M]. San Diego,CA: Academic Press,1999.
[9] 张隆阁,李俊民,陈国培. 利用分数维微积分推广Lyapunov第二方法[J]. 纯粹数学与应用数学.2005,21(3): 291-294.





.jpg)




