- 企业简介
-
作为中国自动化领域的权威旗舰网络媒体,控制网创立于1999年7月,是中国举行的第十四届IFAC (International Federation of Automatic Control)大会的中国官方组织机构的唯一指定网站。控制网是中国自动化学会专家咨询工作 委员会(ECC)的秘书处常设之地。是北京自控在线文化传播有限公司开设的网站。
- 公司类型:其他
- 联系方式
-
- 控制网
- 地址:北京市海淀区上地十街辉煌国际2号楼1504室
- 邮编:100085
- 电话:010-57116291 / 59813326
- 传真:010-59813329
- 网址:http://www.kongzhi.net
- Email:mahongliang@kongzhi.net
- 联系人:市场部
- 案例详细
-
标题 鲁棒组合非线性反馈技术在直流电机速度控制中的应用 技术领域 运动控制 行业 电力 简介 针对带有常量干扰和具有输入饱和约束的直流电机模型,本文通过设计鲁棒组合非线性反馈控制器,来提高电机速度控制的快速性和精确度。基本思想是在组合非线性反馈(Composite Nonlinear Feedback(CNF))控制的基础上加入干扰估计项和补偿项,在消除系统由于干扰产生的稳态误差的同时,保证了原组合非线性反馈控制响应快速及超调小的瞬态性能。 内容 (厦门大学信息与科学技术学院自动化系,福建 厦门 361005周 奇

周奇(1982-)男,湖南长沙人,现就职于厦门大学控制理论与控制工程研究所,主要研究方向为非线性反馈控制。
摘要:针对带有常量干扰和具有输入饱和约束的直流电机模型,本文通过设计鲁棒组合非线性反馈控制器,来提高电机速度控制的快速性和精确度。基本思想是在组合非线性反馈(Composite Nonlinear Feedback(CNF))控制的基础上加入干扰估计项和补偿项,在消除系统由于干扰产生的稳态误差的同时,保证了原组合非线性反馈控制响应快速及超调小的瞬态性能。
关键词:干扰;补偿;非线性;伺服电机;鲁棒组合非线性反馈
Abstract: To achieve fast and accurate set-point tracking of DC motor with constant disturbance and input saturation constraint, in this paper, we design a robust composite nonlinear feedback controller. The basic idea is to add disturbance estimation and compensation into the framework of the original CNF control to eliminate the steady-state bias due to disturbances, and therefore this system retains the fast transient performance of the original CNF control.
Key words: Disturbance; Compensation; Nonlinear; Servo systems; Robust composite nonlinear feedback
直流伺服电机广泛用于各种工业,如机床,线圈络筒机,真空镀膜机和自动焊接机等。常用的控制方法是PID控制,近年来,为了提高伺服电机的性能,出现了多种高级控制方法,例如:模糊控制[1],鲁棒控制[2-4],和自适应控制[5-7]等。
本文采用文献[8]中提出的鲁棒组合非线性反馈控制方法对带有常量干扰的直流伺服电机模型进行控制。组合非线性反馈控制方法最早由Lin[9]提出,它的主要作用是提高具有输入饱和约束的二阶线性闭环系统的瞬态性能。在此基础上,Chen[10]加入可测量的反馈项,使其可以用于更一般的带有饱和输入的系统(不含外部干扰)。当系统加入干扰的时候,组合非线性反馈控制器控制下的系统输出不再渐近匹配参考输入。实际上,伺服电机通常带有干扰,例如摩擦和扭矩偏差所造成的外部干扰。针对该情况,在原有组合非线性反馈控制基础上加入干扰估计项和干扰补偿项,组成鲁棒组合非线性反馈控制器[8]。
本文首先介绍了鲁棒组合非线性反馈控制方法的设计过程,然后介绍直流电机的电流模型,最后采用该控制方法设计直流电机速度控制的鲁棒组合非线性反馈控制器。
1 鲁棒组合非线性反馈控制方法设计过程
鲁棒组合非线性反馈控制方法由Cheng和Peng[8]提出,为了文章的完整性,我们在这一节中简单介绍鲁棒组合非线性反馈控制方法。
考虑带有输入饱和的系统,状态方程如下:
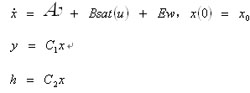 (1)
(1)
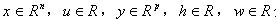 分别表示系统状态,
分别表示系统状态,
控制输入,可测输出和受控输出,以及系统外部干扰。A,B,
C1,C2和E是系统常量矩阵。函数sat: R R表示饱和函数,定义如下:
 (2)
(2)
umax是饱和函数的饱和值。系统满足以下要求。
①(A,B)可镇定。
②(A,C1)可观测。
③(A,B,C2)可逆,s=0不是不变零点。
④ w是未知常量干扰。
⑤ h是y的子集。
首先将常量干扰w当作系统的一个状态变量
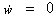 (3)
(3)
并假设w是未知的常量。系统(2)可扩展为
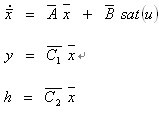 (4)
(4)
而其中可观测。至此,鲁棒组合非线性反馈控制问题便转变成了一般组合非线性反馈控制问题[10],其控制器设计过程如下所述:首先设计带有干扰补偿项的线性反馈部分。
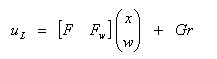 (5)
(5)
满足 ① A+BF是渐近稳定矩阵,② 闭环系统C2 (sI-A-BT)-1满足期望的条件。笔者设计的一般是使其闭环极点中有一个主导极点,满足较小的阻尼比,从而加快闭环系统的响应速度。
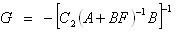 (6)
(6)
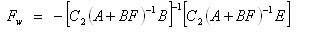 (7)
(7)
然后设计非线性部分,给定正定对称矩阵,解拉普洛夫方程
 (8)
(8)
当(A+BF)为渐近稳定矩阵时候,方程有解。接着,定义
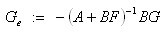 (9)
(9)
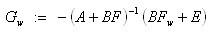 (10)
(10)
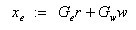 (11)
(11)
从而非线性反馈部分可描述为:
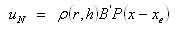 (12)
(12)
其中P(r,h)是|h-r|的一个非正的函数,用来改变闭环系统阻尼比,减少和消除线性反馈部分造成的超调。
综合线性反馈和非线性反馈两部分,鲁棒组合非线性反馈控制器:
 (13)
(13)
注释:文献[8]证明了如下结论:对任意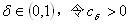 ,令为满足以下条件:
,令为满足以下条件:
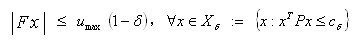 (14)
(14)
的最大标量。对于任意非正的函数p(r,h),如果X。和 r 满足
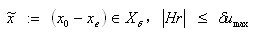 (15)
(15)
则组合非线性反馈控制器(13)和系统(1)构成的闭环系统是渐近稳定的,并且系统受控输出能够渐近跟踪幅值为的阶跃输入。
2 直流电机鲁棒非线性控制器设计
2.1 直流电机模型
根据直流电机模型的传统定义,用下面的电气方程和力学方程描述直流电机的动态模型
 (16)
(16)
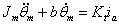 (17)
(17)
其中, 和分别是转子绕组电感和电阻, 电枢电流, 扭转力, 常量转子惯量粘性摩擦系数轴旋转速度输入电压。单位一致的时候, 。定义状态向量,控制输入和控制输出,
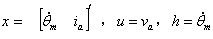
可以得出直流电机的空间状态模型,
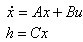 (18)
(18)
并在此基础上考虑扭矩偏差和摩擦产生的常量干扰,式(18)变为
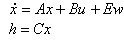 (19)
(19)
其中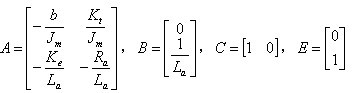 (20)
(20)
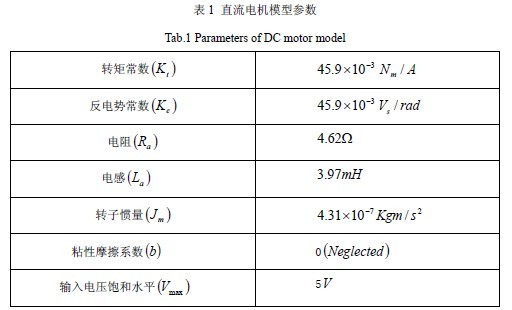
直流电机的一组参数在表1中列出。假设输入电压限制在,直流电机的状态空间方程变为
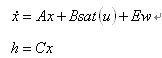 (21)
(21)
其中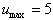 ,矩阵A,B,C和E分别由(20)给出。
,矩阵A,B,C和E分别由(20)给出。
2.2 鲁棒CNF控制器设计
下面给出直流电机速度控制系统(21)的鲁棒CNF控制器设计过程,首先线性反馈增益F为
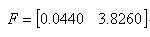
容易验证(A+BF)是稳定的,并去闭环系统的阻尼率为0.4472。因此,可以计算得到前馈增益

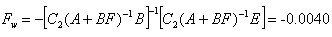
所以鲁棒CNF控制器线性反馈部分
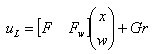
非线性反馈部分为
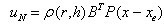
其中p.>0是方程
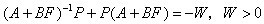
的正定解,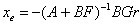 。的选择通常要满足以下两个要求:一方面,当控制输出远离设定值的时候,即的值很大, 选择较小的值,非线性反馈部分作用相应就变小。另一方面,当控制输出接近设定值的时候,即的值很小时, 的值应相应变大,从而加大非线性反馈部分对系统的影响。因此, 的选择不是唯一的。在本文中选择下面的函数
。的选择通常要满足以下两个要求:一方面,当控制输出远离设定值的时候,即的值很大, 选择较小的值,非线性反馈部分作用相应就变小。另一方面,当控制输出接近设定值的时候,即的值很小时, 的值应相应变大,从而加大非线性反馈部分对系统的影响。因此, 的选择不是唯一的。在本文中选择下面的函数
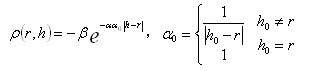 (22)
(22)
设定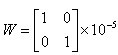 ,得到
,得到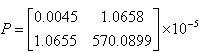 。
。
确定F,G和P后,采用[11]中介绍的计算机辅助设计方法得到α=27和 β =7,
则从而我们可得到鲁棒非线性反馈控制器
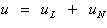
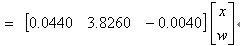
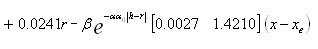 (23)
(23)
其中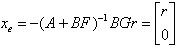
(a)控制输入
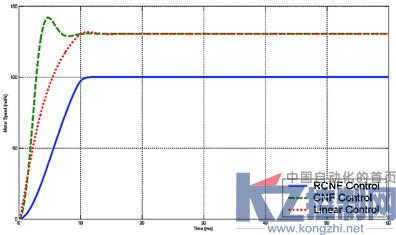
(b)受控输出
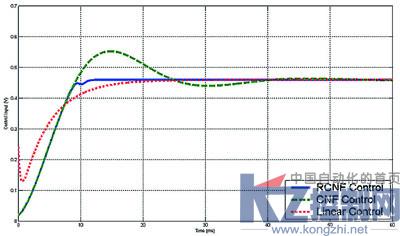
图1 当参考输入r=100rad/s干扰w=250N*m的时候,系统控制输入和受控输出轨迹
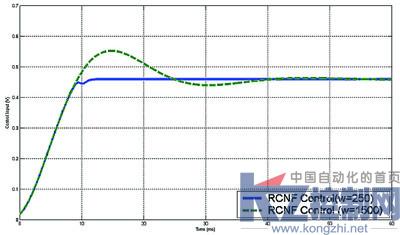
(a)控制输入
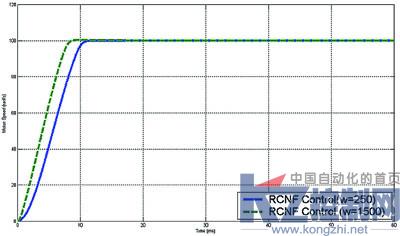
(b)受控输出
图2 当参考输入r=100rad/s干扰w=250N*m和w=1500N*m的时候,系
统控制输入和受控输出轨迹
仿真结果如图1和图2所示:当系统存在误差扭矩干扰的时候,传统反馈控制方法和一般组合非线性反馈控制方法都不能使输出控制达到预定的跟踪效果。但从图1(a)中,我们可以得出在系统常量干扰为250N*m的情况下,普通的线性反馈控制和CNF控制都产生了稳态误差。而鲁棒组合非线性反馈控制使得控制输出很好的跟踪参考输入,同时系统的上升时间为9.3Ms,超调为0.001%,控制输出能取得较为理想的跟踪效果。图2表明鲁棒组合非线性反馈控制在常量干扰为250N*m系统输出的上升时间为9.3Ms,超调为0.001%,当常量干扰为1500N*m的时候,系统输出的上升时间为7.5Ms,超调为0.3%,都表现出很优越的控制性能。
3 结论
鲁棒组合非线性反馈控制在原有的组合非线性反馈基础上加入干扰估计和干扰补偿,不仅保留了原有控制方法的优点,还可以用于带有干扰的系统。利用该方法控制输入饱和系统,使得系统有更好的稳态性能和跟踪性能。仿真和试验结果都表明利用鲁棒组合非线性反馈控制可以快速,准确解决伺服系统控制问题。
因此用该方法控制带有输入饱和约束的系统可以大大提高系统的稳态性能和跟踪性能。
参考文献:
[1] H.Hu, P.-U.Woo: Fuzzy supervisory sliding mode and neural network control for robotic manipulators [J]. IEEE Transaction Industrial Electronics. vol.53,no.3 pp.929-940, June 2006.
[2] G.Cheng, K.Peng, B.M.Chen, T.H.Lee: A microdrive track following controller design suing robust and perfect tracking control with nonlinear compensation [J]. Mechatronics, vol.15, no.8, pp.933-948, 2005.
[3] K.-K.Shyu, C.-K.Lai, Y.-W.Tsai, D.-I.Yang: A newly robust controller design for the position control of permanent-magent synchronous motor [J]. IEEE Transaction Industrial Electronics, vol,49, no.3, pp.558-565, June 2002.
[4] S.Skoczowski, S.Domek, K.Pietrusewicz, B.Broel-Plater: A method for improving the robustness of PID control [J]. IEEE Transaction Industrial Electronics, vol.52, no.6, pp.1669-1676, December 2005.
[5] P.R.Ouyang, W.J.Zhang, M.M.Gupata: An adaptive switching learning control method for trajectory tracking of robot manipulators [J]. Mechatronics,vol.16, no.L, pp.51-61, 2006.
[6] R.-J.Wai, K.-H.Su: Adaptive enhanced fuzzy sliding-mode control for electrical servo drive [J]. IEEE Transaction Industrial Electronics, vol.53, no.2,pp.569-580, April 2006.
[7] H.-J Shieh, F.-J.Lin, P.-K.Huang, L.-T.Teng: Adaptive displacement control with hysteresis modeling for piezo-actuated positioning mechanism [J]. IEEE Transaction Industrial Electronics, vol.53, no.3, pp.905-914, June 2006.
[8] Guoyang Cheng, Kemao Peng: Robust Composite Nonlinear Feedback Control With Application to a Servo Positioning System [J]. IEEE Transactions on Industrial Electronics, Vol. 54, no.2, pp.1132 – 1140, 2007.
[9] Z.Lin,M.Pachter, S.Banda: Toward improvement of tracking performancenonlinear feedback for linear systems [J]. International Journal of Control,vol.70, no.1, pp.1-11, 1998.
[10] B.M.Chen, T.H.Lee, K.Peng, V.Venkataramanan: Composite nonlinear feedback control for linear systems with imput saturation:Theory and an application [J]. IEEE transaction Automation Control, vol.48, no.3, pp.427-439,March 2003.
[11] W.Lan, B.M.Chen: On selection of nonlinear gain in composite nonlinear feedback control for a class of linear systems [J]. Proceedings of the 46th IEEE Conference on Decision and Control, pp.1198-1203, New Orleans LA USA,December 2007.
摘自《自动化博览》2010年第五期





.jpg)




